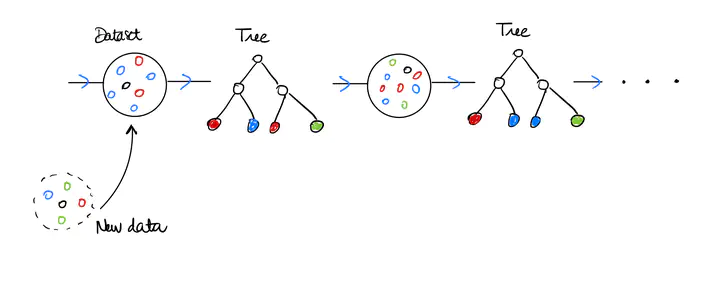
Le Boosting est une méthode d’apprentissage supervisé consistant à bâtir une prédiction fiable en agrégeant les réponses d’apprenants de base, c’est-à-dire d’estimateurs tout juste meilleurs que le hasard. Cette famille d’algorithmes de machine learning construit séquentiellement des apprenants de base, encore appelés faibles ou weak learners. A chaque itération, le nouvel estimateur favorise son apprentissage sur les erreurs du précédent et s’y ajoute pour finalement obtenir un strong learner. Cette méthode a été particulièrement reconnue avec l’algorithme Adaboost (FREUND, SHAPIRE, 1996). Aujourd’hui encore de nombreux challenges sont remportés par des méthodes similaires comme XGBoost/LightGBM (FELLOUS, 2019) réputées puissantes tant sur des modèles de régression que de classification. Le Gradient Boosting proposé par FRIEDMAN (1999 et 2002) est une interprétation du Boosting comme une descente de gradient dans un espace fonctionnel appliquée à un problème d’optimisation dont la fonction objectif est l’erreur en espérance. Cette observation permet d’appliquer la méthode pour un large choix de fonctions de perte comme par exemple l’erreur quadratique en régression ou la fonction logit en classification. Considérons un exemple de weak learner qui constituera notre apprenant de base tout le long de ce cours : l’arbre décisionnel. S’il est peu profond, il est particulièrement simple à mettre en oeuvre et interprétable, en revanche sa pertinence est faible. Comment améliorer ses performances? Augmenter le nombre de noeuds est peu concluant car l’arbre souffre alors d’une variance trop forte. Les méthodes d’agrégation proposent différentes solutions effectives, en générant de multiples versions d’un arbre avant de les combiner. Disposant d’un unique jeu de données, il est alors nécessaire de le perturber pour obtenir des arbres dont les réponses sont différentes mais cohérentes. C’est ce que BREIMAN dénomme perturbing and combining (voir [1]). Dans cet esprit, le Bagging construit chaque arbre à partir d’un échantillon obtenu par bootstrapping : tirage uniforme et avec remise de même taille que le jeu d’entraînement. L’algorithme renvoie la moyenne de la collection d’arbres, estimateur plus robuste, sa variance étant diminuée. Les Forêts aléatoires, procèdent selon le même principe mais les phases d’apprentissage sont réalisées sur des souséchantillons sans remise. La dépendance entre chaque arbre est alors plus faible et par conséquent la variance de leur moyenne également et la réponse plus fiable encore. Venons en au Boosting connu pour surpasser les performances du Bagging et des Forêts alétoires. Comme chaque nouvel arbre apprend des erreurs du précédent et s’y agrège, on peut voir cela comme une diminution du biais. La variance est également améliorée par cet algorithme. Dans [2], il nous est introduit l’algorithme Stochastic Gradient Boosting en injectant de l’aléa par sous échantillonage dans le Grandient Boosting. Les résultats de prédictions peuvent gagner en précision et le coût de calcul est allégé.

On pourra notamment se référer à ce notebook.

Key references

[1] Breiman, Leo. (2000). Bias, Variance , And Arcing Classifiers. Technical Report 460, Statistics Department, University of California
[2] Friedman, Jerome. (2002). Stochastic Gradient Boosting. Computational Statistics & Data Analysis.