KeRF

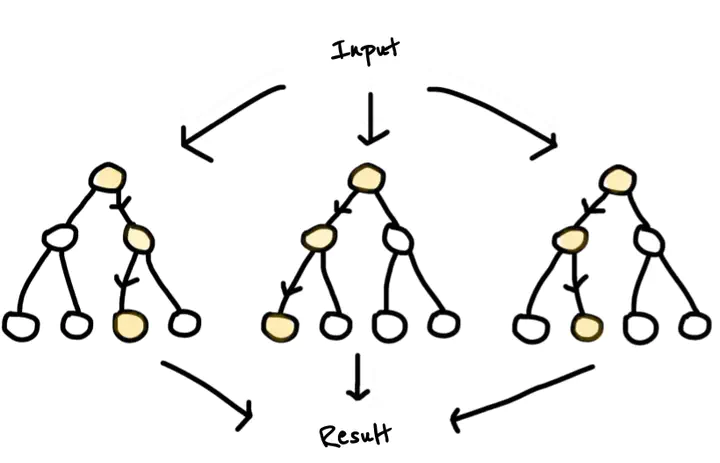
Les forêts aléatoires introduites par Leo Breiman au début des années 2000 sont une méthode de classification et de régression par apprentissage supervisé. L’approche repose sur un principe simple mais puissant, “diviser pour mieux régner” : faire plusieurs sous-échantillonnages des données, construire un arbre de décision pour chaque sous-ensemble selon un paramètre aléatoire, agréger les réponses pour obtenir la prédiction finale. Cette stratégie affiche d’excellents résultats dans divers domaines appliqués, pour en nommer quelques-uns : bio-informatique, économétrie ou encore reconnaissance d’objets 3D. La robustesse des forêts aléatoires dans des problèmes de très grande dimension associée à leur simplicité pratique (peu de paramètres sont à ajuster) en ont fait une méthode populaire. Ce succès contraste avec le peu de résultats théoriques présents dans la littérature. Les forêts demeurent une question mathématique ouverte, ce sont des objets complexes à analyser. Dans le cadre d’un problème de régression, un objectif peut être d’établir le lien entre les forêts aléatoires et des estimateurs à noyau obtenus après une légère modification de leur définition. Cette approche permet d’obtenir de nouveaux estimateurs nommés KeRF (Kernel Random Forest), qui satisfont une certaine proximité aux forêts aléatoires (dans certains cas), tout en ouvrant des perspectives d’analyses mathématiques plus profondes.

XP

Pour cette section, on pourra notamment se référer à ce notebook.

Une comparaison entre KeRF centré, RF centré et RF Breiman évalués sur 2 modèles :

• Modèle 1 :

• Modèle 2 :

On peut également représenter 4 arbres centrés opérant sur un jeu de données indépendantes et identiquement distribuées selon une loi uniforme $\mathcal{U}([0;1]^2)$ :

Contributions : Laure Ferraris, Paul Liautaud