Simulations of the Keller-Segel particle system

We show some simulations of the particle system studied in "Collisions of the supercritical Keller-Segel particle system".

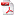
This particle system consists of N point particles in the plane, subjected to Brownian excitation and binary attraction in ΘX/(N|X|2), where X stands for the (vectorial) relative position between two particles and where Θ is a scalar parameter. This system is critical in that
- if Θ<2, the system is subcritical and no cluster does emerge;
- if Θ≥2, the system is supercritical and a macroscopic cluster does emerge.

The above mentioned paper describes the intricate behavior of the particle system, in the supercritical case, before explosion, and in particular which kind of point collisions occur. According to the precise values of N and Θ, there may be either two or three possible kinds of non-sticky collisions.

In all the simulations below, we use an Euler scheme with time step dt and a smoothed interaction, replacing ΘX/(N|X|2) by ΘX/(N(|X|2+ ε)).

In the supercritical case, we carry on the simulation after the macroscopic cluster has emerge, which makes sense thanks to the smoothing parameter ε, even if this is not covered by the theory.


We take N=23 particles and Θ=2.7. The theory says that there are binary, 16-ary and 17-ary non-sticky point collisions, and that the emergence of a cluster containing precisely 18 particles makes explode the system. There are no 3-ary, ..., 15-ary collisions.

The c code, using the time step dt=10-9 and the regularization parameter ε=10-8, writes, every 103 time steps, on each line of the file res.dat,

current time       log10 Z[2]      log10 Z[3]       ...       log10 Z[N],

where Z[i] is defined from the particle configuration (X[1],...,X[N])∈(R2)N (at some given time) as follows.
- For k=1,...,N, and i=2,..,N, let R[k,i] be the square of the distance between X[k] and its (i-1)-th nearest neighbor. If e.g. N=4 and ||X_2-X_3||<||X_2-X_1||<||X_2-X_4||, then R_{2,2}=||X_2-X_3||^2, R_{2,3}=||X_2-X_1||^2 and R_{2,4}=||X_2-X_4||^2.
- Put Z[i]=min(R[1,i],...R[N,i]) for each i=2,...,N.

Observe that Z[i]=0 if and only if there are i particles at the same place.

Here we show the result of a particurarly favorable simulation. We start with i.i.d. N(0,0.2I2) positions. We plot, using gnuplot, 2i+log10 Z[i] as a function of time, for i=2,...,23. We add 2i only to separate the curves.



It seems that there are many binary collisions: the purple curve (the lowest one) dives very often.
It seems that there are a few 3-ary and 4-ary collisions: the green and blue curves have a few dives. This must be numerical.
It seems that there are no 5-ary to 15-ary collisions: the corresponding curves all dive (for the first time) simultaneously, and the red curve (labeled 16) also dives at the same time.
Since at this time the red curve dives and the black one (labeled 17) does not, this seems to really correspond to a 16-ary collision.
A few later, we observe a few non-sticky 17-ary collisions (the black curve labeled 17 dives but the purple curve labeled 18 does not).
A few time later, it seems that some 18-cluster appears forever (the purple curve dives and remains low forever). This is not completely clear, but clearly once the 19-cluster (green curve) has dived, it remains low forever.
Finally, the remaining particles join this cluster, one by one.

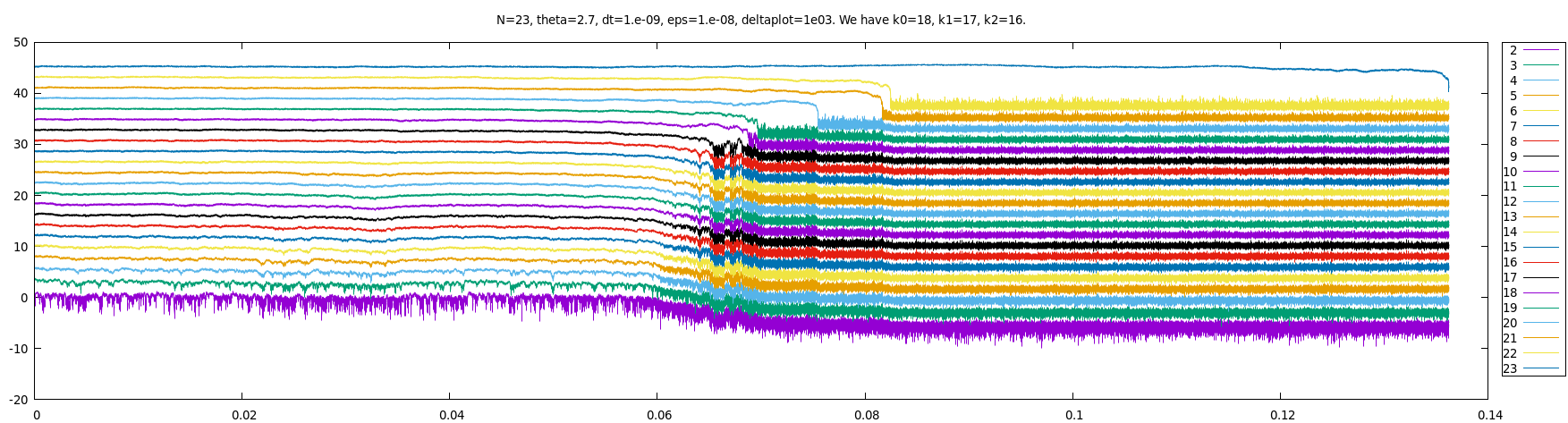
Here is a zoom of the preceeding plot around the explosion time.



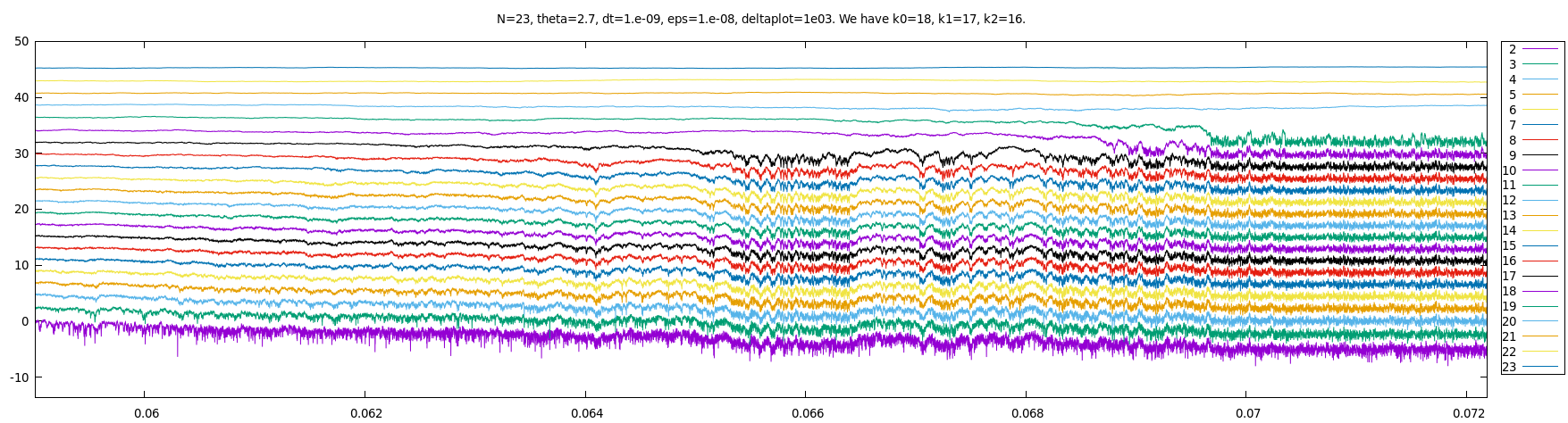
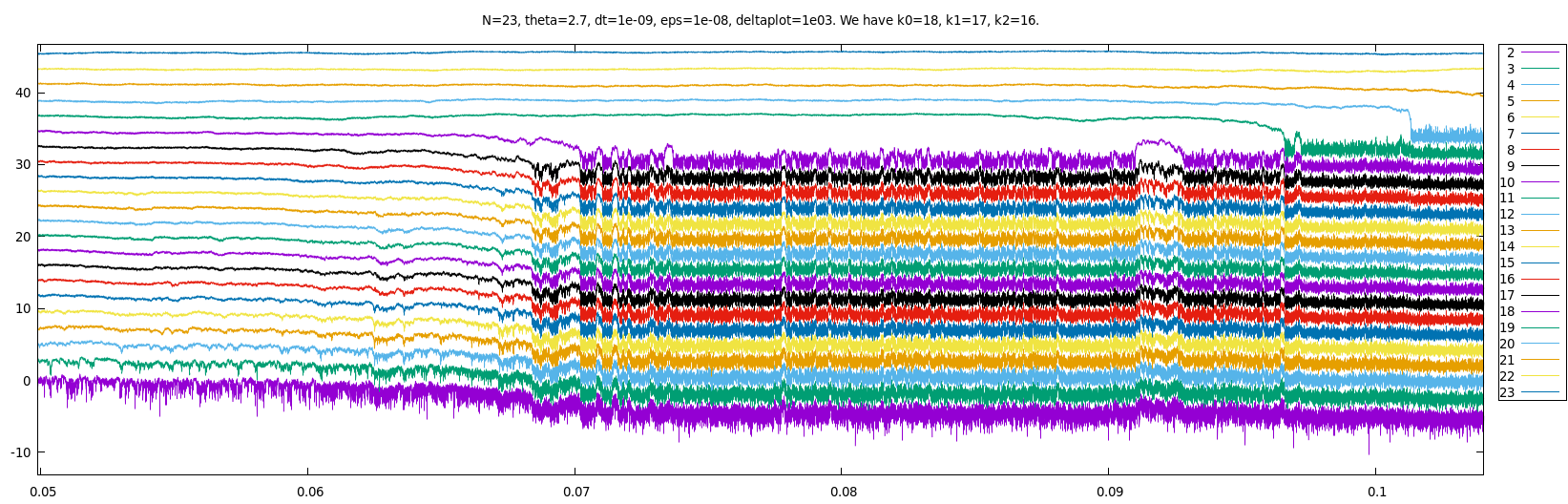
We next show a less favorable simulation (with exactly the same parameters and initial conditions).

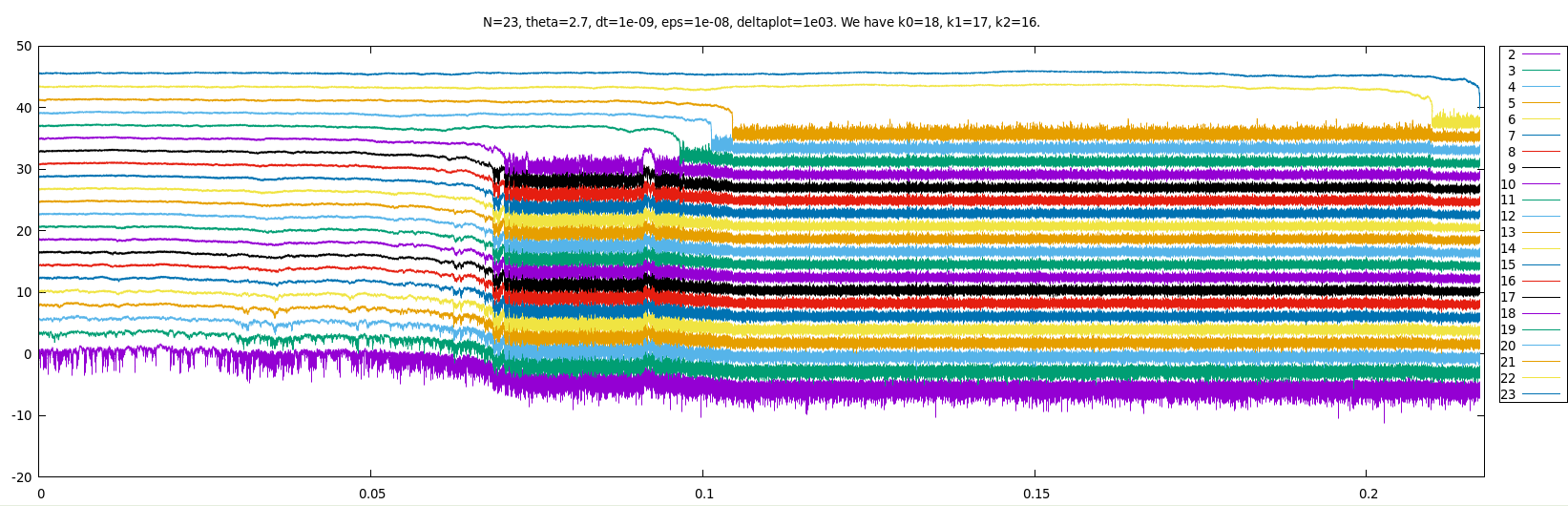
Some defaults: it seems there is no 16-ary collision (but rather something like a 15-ary one) and the 18-cluster (see the purple curve) manages to separate for a short but clearly positive time. Since such a singular particle system is difficult to simulate, it is not surprising to observe such defaults. Again, below a zoom of the above plot around the explosion time.




In all the animations below, produced by this R code, we consider N=100 particles and start with four clouds of particles, we take the time step dt=0.00001 and the regularization parameter ε=0.0001. We use different values for Θ.
Here we are in the subcritical case Θ=1.5, the theory predicts that there are only binary non-sticky point collisions.
Here we consider the slightly supercritical Θ=2.5, the theory predicts that there are only binary and 79-ary non-sticky point collisions, and that the emergence of a cluster containing precisely 80 particles makes explode the system. Due to numerical effects, the final cluster is not perfectly coherent.
Same thing with Θ=2.898, the theory says that there are binary, 68-ary and 69-ary non-sticky point collisions, and that the emergence of a cluster containing precisely 70 particles makes explode the system.
Same thing with Θ=6, the theory says that there are binary and 33-ary non-sticky point collisions, and that the emergence of a cluster containing precisely 34 particles makes explode the system. Here the final cluster is (numerically) perfectly inseparable.
Here Θ=7.5. The theory says that there are binary and 26-ary non-sticky point collisions, and that the emergence of a cluster containing precisely 27 particles makes explode the system. Each initial cloud is composed of 25 particles and is not far from being supercritical, but there is clearly no explosion until the different clouds meet.
Same thing with Θ=8. The theory says that there are binary and 24-ary non-sticky point collisions, and that the emergence of a cluster containing precisely 25 particles makes explode the system. Each initial cloud is critical and should explode, however there are some numerical effects.
Same thing with Θ=10. The theory says that there are binary and 19-ary non-sticky point collisions, and that the emergence of a cluster containing precisely 20 particles makes explode the system. Each initial cloud is supercritical and we indeed observe that each of them explodes. However, still due to numerical effects, we see some particles briefly escaping the clusters.