2. Les tableaux numpy.array

Le module numpy permet de manipuler les tableaux de données, données qui ont toutes le même type numérique. Le nombre de dimension est variable. Ce module est particulièrement optimisé et est au centre de tous les modules de calculs scientifiques en python. Il faut donc connaitre ce module et savoir utiliser la structure numpy.array.

La syntaxe introduite dans numpy est devenue une référence et est utilisée dans les autres modules tels que pytorch ou tensorflow. Ces modules spécialisés dans le deep learning ont recodé les tableaux (appelés tensor) pour pouvoir être utilisés sur GPU (carte graphique) et faire du calcul intensif. Ce n’est pas le cas des numpy.array.

import numpy as np

2.1. Création et propriétés

Création à partir d’une liste de listes. Sans option supplémentaire le type est détecté automatiquement.

a = np.array([[8,3,2,4], [5,1,6,0], [9,7,4,1]])
print(a)

[[8 3 2 4]
 [5 1 6 0]
 [9 7 4 1]]

print("L'objet a est de type:", type(a))
print(f"L'appel a[0] vaut {a[0]} et est de type", type(a[0]))
print(f"L'appel a[0,0] vaut {a[0,0]} et est de type", type(a[0,0]))

L'objet a est de type: <class 'numpy.ndarray'>
L'appel a[0] vaut [8 3 2 4] et est de type <class 'numpy.ndarray'>
L'appel a[0,0] vaut 8 et est de type <class 'numpy.int64'>

Remarque: le type entier utilisé dans numpy est le type numpy.int64 c’est à dire un entier codé sur 64 bits et le nombre le type int par défaut de python.

Quelques champs qui informent sur la structure du tableau a.

print("Dimension:", a.ndim)
print("Taille:", a.size)     # attention len(a) = 3
print("Forme:", a.shape)
print("Types des éléments:", a.dtype) # type des éléments

Dimension: 2
Taille: 12
Forme: (3, 4)
Types des éléments: int64

a.sum() == np.sum(a)       # on peut utiliser la méthode ou une fonction globale

True

Pour changer le type des éléments on peut utiliser la méthode astype:

a.astype('complex')

array([[8.+0.j, 3.+0.j, 2.+0.j, 4.+0.j],
       [5.+0.j, 1.+0.j, 6.+0.j, 0.+0.j],
       [9.+0.j, 7.+0.j, 4.+0.j, 1.+0.j]])

a.astype('float').tolist()      # bien sûr on peut enchaîner les méthodes

[[8.0, 3.0, 2.0, 4.0], [5.0, 1.0, 6.0, 0.0], [9.0, 7.0, 4.0, 1.0]]

2.2. Création à partir de fonctions numpy

np.array([ i+1 for i in range(10) ])

array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10])

np.array([ i+1 for i in range(10) ], dtype='float', ndmin=2)

array([[ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.]])

np.arange(10, 20, step=2)    # même syntaxe que range 

array([10, 12, 14, 16, 18])

Remarque: pour la fonction np.arange on a effectivement création en mémoire de la plage de valeurs alors que range renvoie un objet abstrait itérable (pas de création mémoire).

np.zeros((2, 4))             # de même il y a np.ones

array([[0., 0., 0., 0.],
       [0., 0., 0., 0.]])

La matrice indicatrice s’obtient par la méthode eye.

np.eye(3)

array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

np.diag([1., 2, 3])

array([[1., 0., 0.],
       [0., 2., 0.],
       [0., 0., 3.]])

np.linspace(0, 1, num=6)

array([0. , 0.2, 0.4, 0.6, 0.8, 1. ])

Il faut toujours consuler l’aide disponible. Par exemple consulter la documentation de la fonction np.asarray.

2.3. Dimensions et axes

En numpy les tableaux multidimensionnels sont contruits en utilisant la représentation en ligne (row-major order, cf. page wikipedia).

Ainsi un tableau de dimension 1 peut s’identifier comme un vecteur ligne.

Une matrice (dimension 2) peut se voir comme un tableau de lignes.

u = np.array([1., 4, 10])
a = np.array([[8., 3, 2], [5, 1., 6]])
print("une vecteur ligne: ", u)
print("une matrice: ", a)

une vecteur ligne:  [ 1.  4. 10.]
une matrice:  [[8. 3. 2.]
 [5. 1. 6.]]

u.dtype

dtype('float64')

Le vecteur ligne u a 1 seule dimension, 1 seul axe (axis) de taille 3.

La matrice a a 2 dimensions, 2 axes. Le premier axe (axis 0) est de taille 2 et le deuxième axe est de taille 3.

a[0, 1] # on accède à l'élément d'indice 0 sur le 1er axe et et d'indice 1 sur le 2ème axe

3.0

2.4. Accès aux éléments

2.5. Modification, transformation

• La méthode reshape renvoie une vue du tableau qui l’appelle et ce tableau n’est pas modifié.

• La méthode resize modifie le tableau (change la forme)

a = np.arange(8)
b = a.reshape((2,4))    # renvoie **une vue de a**, a et b partagent les mêmes données
print("a:", a)
print("b:", b)

a: [0 1 2 3 4 5 6 7]
b: [[0 1 2 3]
 [4 5 6 7]]

b[1,1] = 100            # on modifie b: l'élément 5 devient 100
print("a:", a)          # on affiche a 

a: [  0   1   2   3   4 100   6   7]

b.resize((4,2))         # modification in-place
print("b:", b)
print("a:", a)          # a n'est pas modifié

b: [[  0   1]
 [  2   3]
 [  4 100]
 [  6   7]]
a: [  0   1   2   3   4 100   6   7]

Pour ajouter un axe, par exemple pour transformer un vecteur ligne en vecteur colonne on peut utiliser la méthode reshape ou ajouter un axe avec la syntaxe [:, np.newaxis] ou [:, None].

a.T

array([  0,   1,   2,   3,   4, 100,   6,   7])

a.reshape(8, 1) 
a[:, np.newaxis]        # un vecteur ligne transformé en vecteur colonne

array([[  0],
       [  1],
       [  2],
       [  3],
       [  4],
       [100],
       [  6],
       [  7]])

a[:, None]         # le mot clé np.newaxis est équivalent à None

array([[  0],
       [  1],
       [  2],
       [  3],
       [  4],
       [100],
       [  6],
       [  7]])

for i,x in enumerate(b.flat):   # b.flat version "vue" applatie de b 
    print(i, x)

0 0
1 1
2 2
3 3
4 4
5 100
6 6
7 7

c = b.flatten()   # une copie applatie (tous les axes sont écrasés)
c[1] = 50

c

array([  0,  50,   2,   3,   4, 100,   6,   7])

b

array([[  0,   1],
       [  2,   3],
       [  4, 100],
       [  6,   7]])

a

array([  0,   1,   2,   3,   4, 100,   6,   7])

2.6. Opérations

print("moyenne: ", np.mean(a))              # moyenne
print("variance: ", np.var(a))               # version biaisée voir documentation
print("variance sans biais: ", np.var(a, ddof=1))       # version sans biais

moyenne:  15.375
variance:  1027.984375
variance sans biais:  1174.8392857142858

import math
# math.sqrt(a)    # erreur si on execute cette cellule  

np.sqrt(a)              # toujours utiliser les fonctions numpy

array([ 0.        ,  1.        ,  1.41421356,  1.73205081,  2.        ,
       10.        ,  2.44948974,  2.64575131])

np.maximum(a, 4)

array([  4,   4,   4,   4,   4, 100,   6,   7])

np.max(a)

100

2.7. Opérations par axe, option axis

Les opérations par axe sont très importantes et doivent être bien comprises.

print(f"{b.shape[0]} lignes (axe 0) et {b.shape[1]} colonnes (axe 1)")
print(b)
b

4 lignes (axe 0) et 2 colonnes (axe 1)
[[  0   1]
 [  2   3]
 [  4 100]
 [  6   7]]

array([[  0,   1],
       [  2,   3],
       [  4, 100],
       [  6,   7]])

np.sum(b)

123

np.sum(b, axis = 0)       # agit sur l'axe 0: on réduit l'axe 0 -> la somme des lignes 

array([ 12, 111])

np.sum(b, axis = 1)       # agit sur l'axe 1: on réduit l'axe 1 -> la somme des colonnes

array([  1,   5, 104,  13])

np.max(b, axis = 0)

array([  6, 100])

2.7.1. Exercice

On veut calculer

\[ \sum_{k=1}^n k^2 \]

pour différentes valeurs de \(n\), \(n=10,100,1000,10000,100000\).

• Ecrire 2 implémentations différentes: l’une un python sans numpy et l’autre en utilisant numpy.

• Comparer les temps de calculs de ces 2 versions.

def sum_squares_python(n):
    result = 0
    for k in range(n+1):
        result += k**2
    return result

def sum_squares_numpy(n):
    z = np.arange(n+1)
    result = np.sum(z**2)
    return result

for n in 10**np.arange(5):
    print(n)
    %timeit sum_squares_python(n)

Show code cell output Hide code cell output

1

149 ns ± 2.21 ns per loop (mean ± std. dev. of 7 runs, 10,000,000 loops each)
10

361 ns ± 3.03 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)
100

2.96 μs ± 4.91 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
1000

32 μs ± 361 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
10000

362 μs ± 1.52 μs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

for n in 10**np.arange(5):
    print(n)
    %timeit sum_squares_numpy(n)

Show code cell output Hide code cell output

1

1.66 μs ± 20.2 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)
10

1.87 μs ± 252 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
100

1.76 μs ± 7.78 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)
1000

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In[42], line 3
      1 for n in 10**np.arange(5):
      2     print(n)
----> 3     get_ipython().run_line_magic('timeit', 'sum_squares_numpy(n)')

File ~/.venv/lib/python3.11/site-packages/IPython/core/interactiveshell.py:2480, in InteractiveShell.run_line_magic(self, magic_name, line, _stack_depth)
   2478     kwargs['local_ns'] = self.get_local_scope(stack_depth)
   2479 with self.builtin_trap:
-> 2480     result = fn(*args, **kwargs)
   2482 # The code below prevents the output from being displayed
   2483 # when using magics with decorator @output_can_be_silenced
   2484 # when the last Python token in the expression is a ';'.
   2485 if getattr(fn, magic.MAGIC_OUTPUT_CAN_BE_SILENCED, False):

File ~/.venv/lib/python3.11/site-packages/IPython/core/magics/execution.py:1199, in ExecutionMagics.timeit(self, line, cell, local_ns)
   1196         if time_number >= 0.2:
   1197             break
-> 1199 all_runs = timer.repeat(repeat, number)
   1200 best = min(all_runs) / number
   1201 worst = max(all_runs) / number

File /opt/homebrew/Cellar/python@3.11/3.11.11/Frameworks/Python.framework/Versions/3.11/lib/python3.11/timeit.py:208, in Timer.repeat(self, repeat, number)
    206 r = []
    207 for i in range(repeat):
--> 208     t = self.timeit(number)
    209     r.append(t)
    210 return r

File ~/.venv/lib/python3.11/site-packages/IPython/core/magics/execution.py:173, in Timer.timeit(self, number)
    171 gc.disable()
    172 try:
--> 173     timing = self.inner(it, self.timer)
    174 finally:
    175     if gcold:

File <magic-timeit>:1, in inner(_it, _timer)

Cell In[40], line 3, in sum_squares_numpy(n)
      1 def sum_squares_numpy(n):
      2     z = np.arange(n+1)
----> 3     result = np.sum(z**2)
      4     return result

File ~/.venv/lib/python3.11/site-packages/numpy/core/fromnumeric.py:2313, in sum(a, axis, dtype, out, keepdims, initial, where)
   2310         return out
   2311     return res
-> 2313 return _wrapreduction(a, np.add, 'sum', axis, dtype, out, keepdims=keepdims,
   2314                       initial=initial, where=where)

File ~/.venv/lib/python3.11/site-packages/numpy/core/fromnumeric.py:72, in _wrapreduction(obj, ufunc, method, axis, dtype, out, **kwargs)
     71 def _wrapreduction(obj, ufunc, method, axis, dtype, out, **kwargs):
---> 72     passkwargs = {k: v for k, v in kwargs.items()
     73                   if v is not np._NoValue}
     75     if type(obj) is not mu.ndarray:
     76         try:

File ~/.venv/lib/python3.11/site-packages/numpy/core/fromnumeric.py:72, in <dictcomp>(.0)
     71 def _wrapreduction(obj, ufunc, method, axis, dtype, out, **kwargs):
---> 72     passkwargs = {k: v for k, v in kwargs.items()
     73                   if v is not np._NoValue}
     75     if type(obj) is not mu.ndarray:
     76         try:

KeyboardInterrupt: 

2.8. Broadcasting

Mécanisme très utilisé qu’il faut connaitre pour une bonne utilisation! Attention il peut y avoir des pièges.

a = 10 * np.arange(4)    # ou bien np.arange(31, step=10)
b = np.arange(3)
print("a =", a)
print("b =", b)

a = [ 0 10 20 30]
b = [0 1 2]

c = a[:, np.newaxis]
print("c =", c)

c = [[ 0]
 [10]
 [20]
 [30]]

print(c + b)        # broadcasting

[[ 0  1  2]
 [10 11 12]
 [20 21 22]
 [30 31 32]]

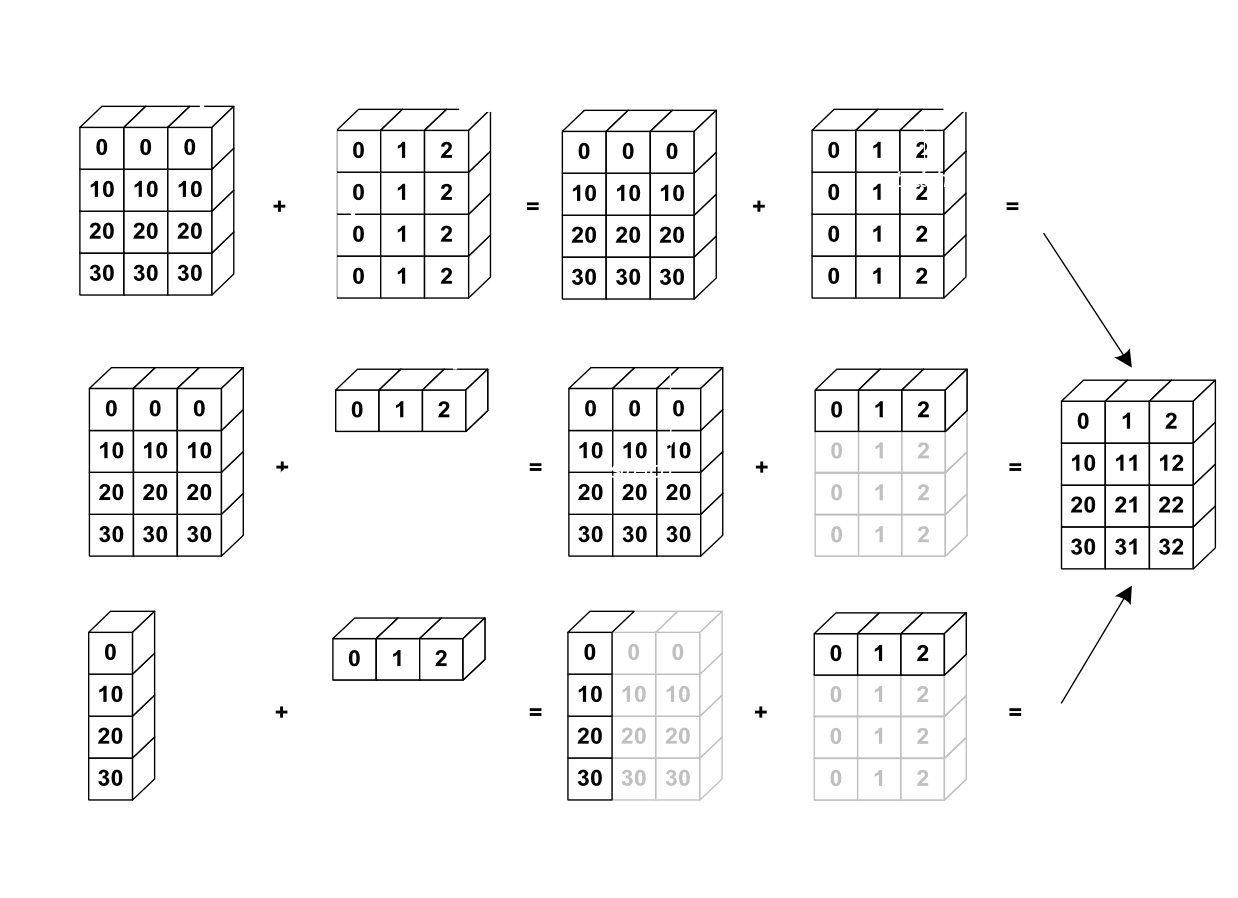
Pour une utilisation avancée du broadcasting (par exemple pour appliquer une fonction qui n’est pas un opérateur arithmétique classique) on peut utiliser np.broadcast

x = np.array([[1], [2], [3]])
y = np.array([40, 50, 60])
b = np.broadcast(x, y)

for u, v in b:
    print(u, v)

1 40
1 50
1 60
2 40
2 50
2 60
3 40
3 50
3 60

b = np.broadcast(x, y)
out = np.empty(b.shape)
out.flat = [u+v for (u,v) in b]
out

array([[41., 51., 61.],
       [42., 52., 62.],
       [43., 53., 63.]])

2.8.1. Exercice

• Construire la matrice

\[\begin{split} A = \begin{pmatrix} 0 & 0 & 0 \\ 10 & 10 & 10 \\ 20 & 20 & 20 \\ 30 & 30 & 30 \end{pmatrix} \end{split}\]

de plusieurs façons différentes: 1. construire un vecteur ligne (1 seul axe) \(u= \begin{pmatrix} 0 & 10 & 20 & 30 \end{pmatrix}\) puis le convertir en vecteur colonne \(v = u^\top\) en utilisant la méthode reshape ou l’ajout d’un axe via np.newaxis, et appeler la fonction np.repeat 2. construire directement le vecteur colonne \(v\) via l’option ndim=2 et la fonction np.repeat 3. construire le vecteur ligne \(u\) puis utiliser np.repeat et ensuite la méthode reshape.

# construction 1. 
u = np.arange(4)*10  # vecteur ligne (1 seul axe 0)

# deux options pour transformer ce vecteur ligne en vecteur colonne:
u.reshape((4, 1))  # on change la forme avec la méthode reshape
u[:, None]         # on ajoute un axe supplémentaire avec cette syntaxe 
# pour plus de lisibilité on peut remplacer le mot-clé None par np.newaxis (c'est pareil!)
v = u[:, np.newaxis]   # écriture un peu plus explicite

# une fois qu'on a un vecteur colonne, on fait une répétition
np.repeat(v, 3, axis=1) # on agit sur l'axe 1 pour faire la répétition

# construction 2.
# il est possible d'utiliser l'option ndmin=2
v = np.array(np.arange(0, 40, step=10), ndmin=2)
v = np.array([i for i in range(0,40,10)], ndmin=2)
np.repeat(v, 3, axis=1) # on agit sur l'axe 1 pour faire la répétition

# construction 3.
u = np.arange(0, 40, step=10)
np.repeat(u, 3).reshape((4, 3))

Show code cell output Hide code cell output

array([[ 0,  0,  0],
       [10, 10, 10],
       [20, 20, 20],
       [30, 30, 30]])

2.9. Algèbre linéaire

En bref:

• inner pour calculer le produit scalaire, on peut aussi utiliser dot ou vdot

• outer pour produit tensoriel entre 2 vecteurs

• opérateur @ pour un produit matriciel, ou la fonction matmul

• pour la transposée d’une matrice a on utilise a.T

• einsum fonction très générale et très optimisée, lire la documention…

Les transformations sont dans le sous-module linalg de numpy

• cholesky factorisation de Cholesky

• qr décomposition QR

• svd décomposition en valeurs singulières

• inv inverse une matrice

• solve résolution d’un système linéaire

Pour en savoir plus il y a:

• Documentation officielle

print(dir(np.linalg))

['LinAlgError', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__', '__package__', '__path__', '__spec__', '_umath_linalg', 'cholesky', 'cond', 'det', 'eig', 'eigh', 'eigvals', 'eigvalsh', 'inv', 'linalg', 'lstsq', 'matrix_power', 'matrix_rank', 'multi_dot', 'norm', 'pinv', 'qr', 'slogdet', 'solve', 'svd', 'tensorinv', 'tensorsolve', 'test']

u = np.arange(4)
v = 2+u
print("u =", u, "\nv =", v)

u = [0 1 2 3] 
v = [2 3 4 5]

np.inner(u, v) == np.sum(u*v)

True

A = np.outer(u, v)
print(A)

[[ 0  0  0  0]
 [ 2  3  4  5]
 [ 4  6  8 10]
 [ 6  9 12 15]]

print("attention au produit: \n", A * u)
print("voici le produit matrice-vecteur: \n", A @ u)

attention au produit: 
 [[ 0  0  0  0]
 [ 0  3  8 15]
 [ 0  6 16 30]
 [ 0  9 24 45]]
voici le produit matrice-vecteur: 
 [ 0 26 52 78]

A.T @ u

array([28, 42, 56, 70])