4. Réduction de variance et calcul de sensibilités#
Sur on problème de modélisation classique en assurance, on illustre l’importance de l’erreur relative puis deux techniques de réduction de variance:
méthode par préconditionnement,
échantillonage d’importance (important pour les événements rares).
Dans une deuxième partie on s’intéresse aux sensibilités et comment implémenter efficacement la méthode des différences finies avec la méthode de Monte Carlo.
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme()
from numpy.random import default_rng
rng = default_rng()
4.1. Charge sinistre et loi Poisson-composée#
On définit la charge sinistre totale (sur une période \(T\)) par la variable aléatoire positive
où \(N\) est une variable aléatoire à valeurs dans \(\mathbf{N}\) représentant le nombre de sinistres sur la période \(T\), et pour \(i \ge 1\), \(X_i\) est une variable aléatoire à valeurs dans \(\mathbf{R}_+\) représentant le coût du i-ème sinistre, avec la convention selon laquelle la somme est nulle si \(N = 0\). Les \((X_i)_{i \ge 1}\) sont supposées indépendantes et identiquement distribuées, et indépendantes de \(N\) (indépendance fréquences - coûts).
Une modélisation classique est de considérer
\(N\) de loi de Poisson de paramètre \(\lambda > 0\),
\(X_1\) de loi log-normale de paramètres \(\mu > 0\), \(\sigma^2 > 0\), c’est à dire \(X_1 = \exp(G_1)\) avec \(G_1 \sim \mathcal{N}(\mu, \sigma^2)\).
Le but est d’estimer la probabilité de dépassement c’est à dire calculer la probabilité que la charge sinistre totale dépasse un seuil \(K\):
Dans la suite on prend \(\lambda = 10\), \(\mu = 0.1\) et \(\sigma = 0.3\) et on considère plusieurs valeurs du seuil \(K\).
4.1.1. Question: simulation de la charge sinistre totale#
Ecrire une fonction simu_S(size, mu, sigma, lambd) qui renvoie un échantillon de taille size de réalisations indépendantes de \(S\).
def simu_S(size, mu, sigma, lambd):
sample_N = rng.poisson(size=size, lam=lambd)
sample_S = np.empty(size)
for k, Nk in enumerate(sample_N):
sample_S[k] = np.sum(rng.lognormal(size=Nk, mean=mu, sigma = sigma))
return sample_S
lambd, mu, sigma = 10, 0.1, 0.3
simu_S(10, mu, sigma, lambd)
array([14.09776308, 11.07957294, 8.97478688, 15.82168176, 16.41027638,
7.32630634, 7.26381791, 16.40386963, 8.2264309 , 13.68570782])
4.1.2. Question: représentation graphique#
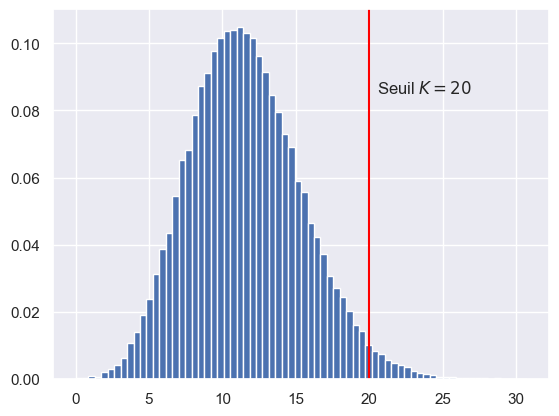
Représenter l’histogramme d’un échantillon de \(100\,000\) réalisations de \(S\) et du seuil \(K = 20\) par une ligne verticale rouge.
sample_S = simu_S(int(1e5), mu, sigma, lambd)
K = 20
fig, ax = plt.subplots()
ax.hist(sample_S, bins=70, density=True)
ax.axvline(K, color='red')
ax.text(K+.5, 0.085, fr'Seuil $K={K}$', size=12)
plt.show()
4.2. Estimateur Monte Carlo et erreur relative#
Soit \(p_n = \displaystyle \frac{1}{n} \sum_{j=1}^n \mathbf{1}_{S^{(j)} > K}\) l’estimateur Monte Carlo de \(p= \mathbf{P}\bigl[S > K\bigr]\) où \((S^{(j)})_{j=1,\dots,n}\) est une suite i.i.d. de même loi que \(S\).
On rappelle que:
l’erreur absolue de l’estimateur Monte Carlo \(p_n\) est définie par \(|p_n - p|\) et qu’avec probabilité 0.95 cette erreur est bornée par \(e_n = 1.96 \frac{\sigma_n}{\sqrt{n}}\) avec \(\sigma_n^2 = p_n - p_n^2\),
l’erreur relative de l’estimateur Monte Carlo est définie par \(\frac{|p_n - p|}{p}\) que l’on majore avec probabilité 0.95 par \(\frac{e_n}{p_n}\).
4.2.1. Question: erreur relative#
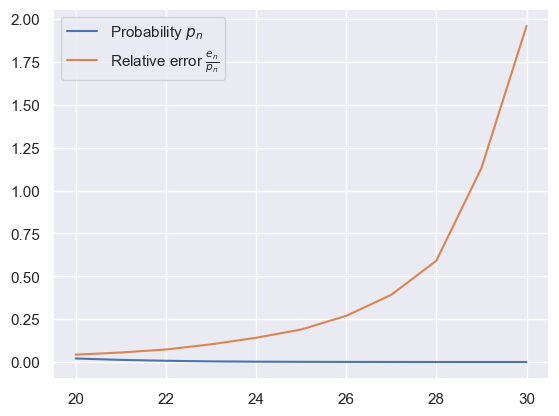
Ecrire une fonction relative_error qui à partir d’un échantillon de \(S\) (de taille \(n\)) et d’une valeur de seuil \(K\) renvoie la probabilité \(p_n\) et l’erreur relative (plus exactement la borne \(\frac{e_n}{p_n}\) à 95%).
Tracer l’erreur relative d’un échantillon de taille \(100\,000\) en fonction de \(K\) pour \(K\) allant de 20 à 30. Comment interpréter cette courbe?
def relative_error(sample, K):
p_n = np.mean(sample > K)
v_n = p_n - p_n**2
e_n = 1.96 * np.sqrt(v_n / sample.size)
return p_n, e_n / p_n
Ks = np.arange(20, 31)
errors = np.array([relative_error(sample_S, K) for K in Ks])
fig, ax = plt.subplots()
ax.plot(Ks, errors)
ax.legend((r'Probability $p_n$',r'Relative error $\frac{e_n}{p_n}$'))
plt.show()
4.2.2. Question: Monte Carlo à précision fixée#
Mettre en oeuvre un estimateur de Monte Carlo qui s’arrête dès que l’erreur relative est de 5%. On pourra par exemple introduire la variable aléatoire
qui dépend d’un paramètre \(m\) fixé, par exemple \(m = 10\,000\), et renvoyer \(p_{\tau^{(m)}}\) ainsi que l’erreur relative et la taille de l’estimateur associé. Le paramètre \(m\) permet de recalculer l’estimateur et l’erreur uniquement toutes les \(m\) itérations et donc de réduire la complexité par rapport au choix naïf \(m = 1\). On appelle ce paramètre \(m\) la taille du batch (size batch). Le nombre d’itérations (la taille de l’échantillon) dans la méthode de Monte Carlo pour un \(\tau^{(m)}\) donné est donc \(\tau^{(m)} \times m\).
Définir la fonction qui code cet estimateur Monte Carlo:
monte_carlo_relative(mu, sigma, lambd, K, size_batch = 10000, error = 0.05)
def monte_carlo_relative(mu, sigma, lambd, K, size_batch = 10000, error = 0.05):
sample_S = simu_S(size_batch, mu, sigma, lambd)
while True:
p_n, er_n = relative_error(sample_S, K)
if er_n < error:
return p_n, er_n, len(sample_S)
else:
new_sample = simu_S(size_batch, mu, sigma, lambd)
sample_S = np.append(sample_S, new_sample)
4.2.3. Question: complexité en fonction de \(K\)#
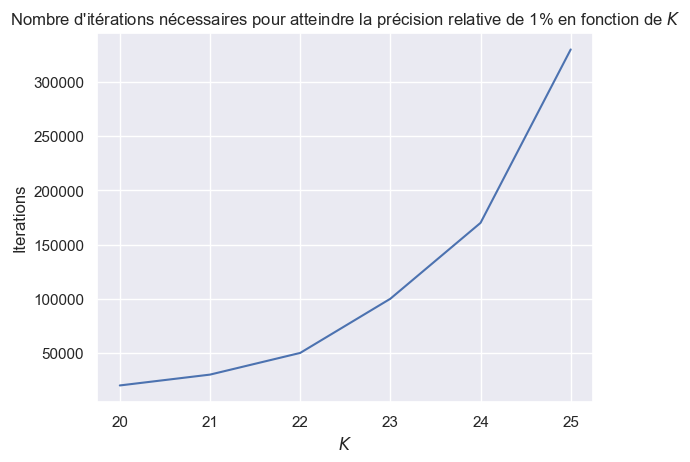
Reproduire un tableau de résultat similaire au tableau suivant obtenu avec cet estimateur de Monte Carlo adaptatif jusqu’à l’itération \(\tau^{(m)} \times m\) pour une erreur relative de 10% et pour différentes valeurs de \(K = 20,\dots,25\).
Tracer le nombre d’itérations nécessaires en fonction de \(K\).
import pandas as pd
df = pd.read_pickle("data/iterations_df.pkl")
df
| Probabilité $p_n$ | Erreur relative | Itérations | |
|---|---|---|---|
| 20 | 0.021600 | 0.093277 | 20000 |
| 21 | 0.013100 | 0.098219 | 30000 |
| 22 | 0.007820 | 0.098733 | 50000 |
| 23 | 0.003910 | 0.098927 | 100000 |
| 24 | 0.002259 | 0.099908 | 170000 |
| 25 | 0.001258 | 0.099186 | 310000 |
Ks = np.arange(20, 26)
result = np.array([monte_carlo_relative(mu, sigma, lambd, K, error = 0.1) for K in Ks])
import pandas as pd
res_df = pd.DataFrame(result,
columns=("Probabilité $p_n$", "Erreur relative", "Itérations"),
index = Ks)
res_df = res_df.astype({'Itérations': 'int'})
res_df
#res_df.to_pickle("data/iterations_df.pkl")
| Probabilité $p_n$ | Erreur relative | Itérations | |
|---|---|---|---|
| 20 | 0.022000 | 0.092406 | 20000 |
| 21 | 0.012733 | 0.099642 | 30000 |
| 22 | 0.007740 | 0.099246 | 50000 |
| 23 | 0.003990 | 0.097927 | 100000 |
| 24 | 0.002271 | 0.099648 | 170000 |
| 25 | 0.001200 | 0.098435 | 330000 |
fig, ax = plt.subplots()
ax.plot(Ks, res_df['Itérations'], label="Iterations")
ax.set_xlabel(r"$K$")
ax.set_ylabel(r"Iterations")
ax.set_title(r"Nombre d'itérations nécessaires pour atteindre la précision relative de 1% en fonction de $K$")
plt.show()
4.3. Réduction de variance par préconditionnement#
Pour réduire la variance on teste d’abord l’idée présentée dans l’exercice 1 du TD3, c’est à dire qu’on considère la variable aléatoire
et la représentation suivante
4.3.1. Question: simulation de \(M\)#
Ecrire une fonction simu_M similaire à la fonction simu_S avec l’argument \(K\) supplémentaire qui renvoie un échantillon i.i.d. de même loi que \(M\).
def simu_M(size, mu, sigma, lambd, K):
def one_M():
sum_Xi = rng.lognormal(size=1, mean=mu, sigma = sigma)
r = 1
while sum_Xi <= K:
sum_Xi += rng.lognormal(size=1, mean=mu, sigma = sigma)
r += 1
return r
sample_M = np.array([ one_M() for _ in range(size) ])
return sample_M
# la fonction précédente est correcte mais trop lente car il y a de très
# nombreux appels successifs au générateur de taille size=1 ce qui est
# à éviter. voici une version plus optimisée
def simu_M(size, mu, sigma, lambd, K, batch_size=20):
def one_M():
sample_x = np.zeros(1)
while True:
sample_x = np.append(sample_x,
rng.lognormal(size=batch_size, mean=mu, sigma = sigma))
r = np.argmax(np.cumsum(sample_x) > K)
if r > 0: return r
return r
sample_M = np.array([ one_M() for _ in range(size) ])
return sample_M
# exercice: faire un code similaire sans "grossir" sample_x avec np.append
4.3.2. Question: Monte Carlo et ratio de variance#
En utilisant la fonction monte_carlo du TP précédent. Calculer le ratio de variance entre l’estimateur \(p_n\) et l’estimateur basé sur la représentation \(p = \mathbf{E}[\phi(M)]\) où \(\phi\) est calculée en utilisant la fonction de survie et la fonction de masse de la loi de Poisson (cf. la documentation de stats.poisson). Faire ce calcul pour différentes valeurs de \(K\) et \(n = 20\,000\)
def monte_carlo(sample, proba = 0.95):
mean = np.mean(sample)
var = np.var(sample, ddof=1)
alpha = 1 - proba
quantile = stats.norm.ppf(1 - alpha/2) # fonction quantile
ci_size = quantile * np.sqrt(var / sample.size)
return (mean, var, mean - ci_size, mean + ci_size)
Ks = np.arange(20,30)
sample_S = simu_S(int(1e6), mu, sigma, lambd)
result = [ monte_carlo(sample_S > K) for K in Ks ]
import pandas as pd
res_df = pd.DataFrame(result,
columns=["mean", "var", "lower", "upper"],
index=Ks)
res_df
| mean | var | lower | upper | |
|---|---|---|---|---|
| 20 | 0.021313 | 0.020859 | 0.021030 | 0.021596 |
| 21 | 0.012691 | 0.012530 | 0.012472 | 0.012910 |
| 22 | 0.007350 | 0.007296 | 0.007183 | 0.007517 |
| 23 | 0.004095 | 0.004078 | 0.003970 | 0.004220 |
| 24 | 0.002211 | 0.002206 | 0.002119 | 0.002303 |
| 25 | 0.001157 | 0.001156 | 0.001090 | 0.001224 |
| 26 | 0.000566 | 0.000566 | 0.000519 | 0.000613 |
| 27 | 0.000289 | 0.000289 | 0.000256 | 0.000322 |
| 28 | 0.000163 | 0.000163 | 0.000138 | 0.000188 |
| 29 | 0.000084 | 0.000084 | 0.000066 | 0.000102 |
def phi(m, lambd = 10):
N = stats.poisson(mu = lambd)
return N.pmf(m) + N.sf(m)
result = []
for K in Ks:
sample_M = simu_M(int(2e4), mu, sigma, lambd, K)
result.append(monte_carlo(phi(sample_M)))
import pandas as pd
res_df_precond = pd.DataFrame(result,
columns=["mean", "var", "lower", "upper"],
index=Ks)
res_df_precond
| mean | var | lower | upper | |
|---|---|---|---|---|
| 20 | 0.021242 | 3.614600e-04 | 0.020979 | 0.021506 |
| 21 | 0.012557 | 1.520196e-04 | 0.012387 | 0.012728 |
| 22 | 0.007175 | 6.044536e-05 | 0.007067 | 0.007282 |
| 23 | 0.004072 | 2.595323e-05 | 0.004002 | 0.004143 |
| 24 | 0.002213 | 8.909738e-06 | 0.002172 | 0.002254 |
| 25 | 0.001164 | 2.932395e-06 | 0.001141 | 0.001188 |
| 26 | 0.000593 | 9.563623e-07 | 0.000580 | 0.000607 |
| 27 | 0.000305 | 3.470546e-07 | 0.000297 | 0.000313 |
| 28 | 0.000148 | 8.699580e-08 | 0.000144 | 0.000152 |
| 29 | 0.000072 | 2.925556e-08 | 0.000069 | 0.000074 |
res_df["var"] / res_df_precond["var"]
20 57.707013
21 82.423248
22 120.703797
23 157.137846
24 247.607030
25 394.101943
26 591.491545
27 832.482180
28 1873.350162
29 2871.010676
Name: var, dtype: float64
4.4. Réduction de variance par échantillonage d’importance#
Pour réduire la variance sans faire exploser la complexité pour les grandes valeurs de \(K\) on propose une méthode d’échantillonage d’importance (Importance Sampling) en modifiant la loi de la variable aléatoire \(N\) (on peut faire un autre choix, en changeant la loi des \(X_i\) ou bien en changeant la loi de \(N\) et des \(X_i\)). Le changement de loi proposé ici repose sur le changement de probabilité, pour \(\theta \in \mathbf{R}\)
où \(\psi(\theta) = \log \mathbf{E} \bigl[ \exp(\theta N) \bigr] = \lambda (e^\theta - 1)\). On vérifie par le calcul que la loi de \(N\) sous \(\mathbf{P}_\theta\) est la loi de Poisson de paramètre \(\tilde \lambda = \lambda e^\theta\). Ainsi on a la représentation
Il est d’usage pour la loi de Poisson d’écrire la variable \(L_\theta\) à partir de \(\lambda\) et \(\tilde \lambda\) (la valeur du paramètre de la loi de Poisson sous la nouvelle probabilité) i.e.
4.4.1. Question: simulation sous \(\mathbf{P}_\theta\)#
La loi de \(N\) sous \(\mathbf{P}_\theta\) est la loi de Poisson de paramètre \(\tilde \lambda=\lambda e^\theta\) et la suite \((X_i)_{i \ge 1}\) est indépendante de \(N\) donc de \(L_\theta\) et n’est donc pas impactée par le changement de probabilité: la loi des \((X_i)_{i \ge 1}\) est inchangée.
Ecrire une fonction simu_S_tilde inspirée de simu_S qui prend un paramètre supplémentaire \(\theta\) et qui renvoie un échantillon de \(\sum_{i=1}^{N} X_i\) sous \(\mathbf{P}_\theta\).
def simu_S_tilde(size, mu, sigma, lambd, theta):
sample_N_tilde = rng.poisson(size=size, lam=lambd * np.exp(theta))
sample_sum = np.empty(size)
for k, Nk in enumerate(sample_N_tilde):
sample_sum[k] = np.sum(rng.lognormal(size=Nk, mean=mu, sigma = sigma))
return sample_sum
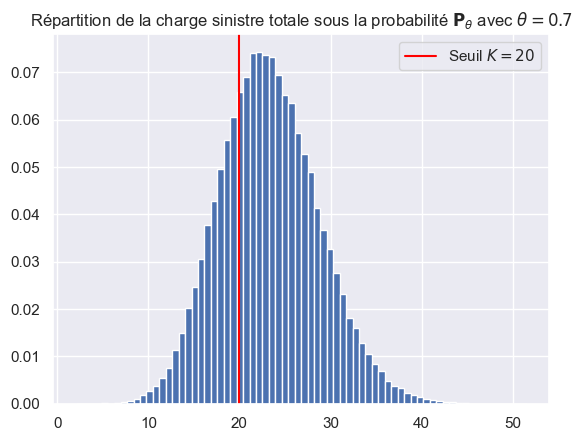
theta = 0.7
sample_S = simu_S_tilde(int(1e5), mu, sigma, lambd, theta=theta)
K = 20
fig, ax = plt.subplots()
ax.hist(sample_S, bins=70, density=True)
ax.axvline(K, color='red', label=fr'Seuil $K={K}$')
ax.set_title(fr"Répartition de la charge sinistre totale sous la probabilité $\mathbf{{P}}_\theta$ avec $\theta = {theta}$")
ax.legend()
plt.show()
4.4.2. Question: Monte Carlo sous \(\mathbf{P}_\theta\)#
Comparer pour différentes valeurs de \(K\), avec \(\theta = 0.7\), l’estimateur de Monte Carlo basé sur la représentation
Pour \(K = 22\) le ratio de variance est de l’ordre de 16-17.
Que se passe-t-il si le paramètre \(\theta\) est mal choisi? (prendre par exemple \(\theta = 1.2\) puis \(\theta = 1.5\), et \(\theta = -0.1\)…)
# on modifie un peu la fonction précédente car on a besoin de N_tilde !
def simu_sous_P_tilde(size, mu, sigma, lambd, theta):
sample_N_tilde = rng.poisson(size=size, lam=lambd * np.exp(theta))
sample_sum = np.empty(size)
for k, Nk in enumerate(sample_N_tilde):
sample_sum[k] = np.sum(rng.lognormal(size=Nk, mean=mu, sigma = sigma))
return sample_sum, sample_N_tilde
from math import log
# on modifie un peu la fonction précédente car on a besoin de N_tilde !
def simu_sous_P_tilde(size, mu, sigma, lambd, theta):
#sample_N = np.full((size,), fill_value=15)
sample_N = rng.poisson(size=size, lam=lambd)
sample_sum = np.empty(size)
sample_correction = np.empty(size)
for k, Nk in enumerate(sample_N):
if Nk > 0: # and Nk < 15:
theta = 8*(1./(Nk**(2.))) #(1/sigma)*(0.8*log(20)-np.sqrt(log(Nk))-mu-0.5*sigma**2)
sample_Gi = theta + rng.standard_normal(size=Nk)
sample_sum[k] = np.sum(np.exp(mu + sigma*sample_Gi))
sample_correction[k] = (np.exp(-np.sum(theta*sample_Gi) + Nk*0.5*theta**2)) #**(1/Nk)
#else:
# sample_Gi = rng.standard_normal(size=Nk)
# sample_sum[k] = np.sum(np.exp(mu + sigma*sample_Gi))
return sample_sum, sample_correction
theta = 0.6
sample_S,_ = simu_sous_P_tilde(int(1e5), mu, sigma, lambd, theta=theta)
K = 20
fig, ax = plt.subplots()
ax.hist(sample_S, bins=70, density=True)
ax.axvline(K, color='red', label=fr'Seuil $K={K}$')
ax.set_title(fr"Répartition de la charge sinistre totale sous la probabilité $\mathbf{{P}}_\theta$ avec $\theta = {theta}$")
ax.legend()
plt.show()
Ks = np.arange(20,30)
theta = 0.6
#lambd_tilde = lambd * np.exp(theta)
sample_sum, sample_correction = simu_sous_P_tilde(int(1e6), mu, sigma, lambd, theta)
result = []
for K in Ks:
sample = (sample_sum > K) * sample_correction #(lambd / lambd_tilde)**sample_N_tilde * np.exp(lambd_tilde - lambd)
result.append(monte_carlo(sample))
import pandas as pd
res_df_is = pd.DataFrame(result,
columns=["mean", "var", "lower", "upper"],
index=Ks)
res_df_is
| mean | var | lower | upper | |
|---|---|---|---|---|
| 20 | 0.021342 | 0.019279 | 0.021070 | 0.021614 |
| 21 | 0.012683 | 0.011535 | 0.012472 | 0.012893 |
| 22 | 0.007343 | 0.006710 | 0.007182 | 0.007504 |
| 23 | 0.004045 | 0.003703 | 0.003926 | 0.004164 |
| 24 | 0.002193 | 0.002009 | 0.002105 | 0.002281 |
| 25 | 0.001183 | 0.001083 | 0.001119 | 0.001248 |
| 26 | 0.000605 | 0.000555 | 0.000559 | 0.000652 |
| 27 | 0.000291 | 0.000265 | 0.000259 | 0.000322 |
| 28 | 0.000139 | 0.000128 | 0.000117 | 0.000161 |
| 29 | 0.000073 | 0.000067 | 0.000057 | 0.000089 |
res_df
| mean | var | lower | upper | |
|---|---|---|---|---|
| 20 | 0.021313 | 0.020859 | 0.021030 | 0.021596 |
| 21 | 0.012691 | 0.012530 | 0.012472 | 0.012910 |
| 22 | 0.007350 | 0.007296 | 0.007183 | 0.007517 |
| 23 | 0.004095 | 0.004078 | 0.003970 | 0.004220 |
| 24 | 0.002211 | 0.002206 | 0.002119 | 0.002303 |
| 25 | 0.001157 | 0.001156 | 0.001090 | 0.001224 |
| 26 | 0.000566 | 0.000566 | 0.000519 | 0.000613 |
| 27 | 0.000289 | 0.000289 | 0.000256 | 0.000322 |
| 28 | 0.000163 | 0.000163 | 0.000138 | 0.000188 |
| 29 | 0.000084 | 0.000084 | 0.000066 | 0.000102 |
theta = 0.0
monte_carlo(sample_correction)
(0.9987815808560006,
0.3287286471465458,
0.9976578381980953,
0.9999053235139058)
sample_correction
array([1.13245804, 1.33812404, 1.15581769, ..., 1.00651544, 0.75924434,
0.70531721])
?np.full
monte_carlo(1./sample_correction)
/var/folders/z7/f1cycb2x0wvfx05bszkps2l80000gn/T/ipykernel_5452/2518965363.py:1: RuntimeWarning: divide by zero encountered in divide
monte_carlo(1./sample_correction)
/Users/lemaire/.venv/lib/python3.11/site-packages/numpy/core/_methods.py:173: RuntimeWarning: invalid value encountered in subtract
x = asanyarray(arr - arrmean)
(inf, nan, nan, nan)
Ks = np.arange(20,26)
theta = 0.0
#lambd_tilde = lambd * np.exp(theta)
sample_sum, sample_correction = simu_sous_P_tilde(int(2e6), mu, sigma, lambd, theta)
result = []
for K in Ks:
sample = (sample_sum > K) * sample_correction #(lambd / lambd_tilde)**sample_N_tilde * np.exp(lambd_tilde - lambd)
result.append(monte_carlo(sample))
import pandas as pd
res_df_is = pd.DataFrame(result,
columns=["mean", "var", "lower", "upper"],
index=Ks)
res_df_is
| mean | var | lower | upper | |
|---|---|---|---|---|
| 20 | 0.021210 | 0.019161 | 0.021018 | 0.021402 |
| 21 | 0.012528 | 0.011394 | 0.012380 | 0.012676 |
| 22 | 0.007136 | 0.006515 | 0.007024 | 0.007248 |
| 23 | 0.003978 | 0.003637 | 0.003895 | 0.004062 |
| 24 | 0.002159 | 0.001974 | 0.002097 | 0.002220 |
| 25 | 0.001141 | 0.001042 | 0.001097 | 0.001186 |
res_df
| mean | var | lower | upper | |
|---|---|---|---|---|
| 20 | 0.021313 | 0.020859 | 0.021030 | 0.021596 |
| 21 | 0.012691 | 0.012530 | 0.012472 | 0.012910 |
| 22 | 0.007350 | 0.007296 | 0.007183 | 0.007517 |
| 23 | 0.004095 | 0.004078 | 0.003970 | 0.004220 |
| 24 | 0.002211 | 0.002206 | 0.002119 | 0.002303 |
| 25 | 0.001157 | 0.001156 | 0.001090 | 0.001224 |
| 26 | 0.000566 | 0.000566 | 0.000519 | 0.000613 |
| 27 | 0.000289 | 0.000289 | 0.000256 | 0.000322 |
| 28 | 0.000163 | 0.000163 | 0.000138 | 0.000188 |
| 29 | 0.000084 | 0.000084 | 0.000066 | 0.000102 |
res_df["var"] / res_df_is["var"]
20 1.088630
21 1.099665
22 1.119867
23 1.121446
24 1.117406
25 1.109577
26 NaN
27 NaN
28 NaN
29 NaN
Name: var, dtype: float64
4.5. Calcul de sensibilités#
On utilisera la notation \(S^{(\lambda)}\) pour indiquer la dépendance de variable aléatoire \(S = \sum_{i=1}^{N} X_i\) en le paramètre \(\lambda > 0\) (paramètre de la loi de Poisson sous-jacente). On s’intéresse à la sensibilité de la probabilité \(p\) en fonction de lambda c’est à dire
4.5.1. Différences finies#
Implémenter l’estimateur Monte Carlo basé sur les différences finies d’ordre 2
Comme vu en cours, il y a plusieurs façon d’implémenter l’estimateur Monte Carlo dans ce cadre biaisé.
Le premier estimateur naïf \(J^{(1)}_{n,h}(\lambda)\) est basé sur des réalisations indépendantes de \(S^{(\lambda+h)}\) et \(S^{(\lambda-h)}\) et n’est pas efficace: la variance explose lorsque \(h\) tend vers 0. Ainsi on pose
où \((S^{(\lambda+h)}_k)_{k \ge 1}\) et \((\tilde S^{(\lambda-h)}_k)_{k \ge 1}\) sont des suites indépendantes de variables aléatoires i.i.d..
Le deuxième estimateur \(J^{(2)}_{n,h}(\lambda)\) utilise des réalisations fortements corrélées de la loi de Poisson au sens suivant: on utilise la même réalisation uniforme \(U\) pour constuire deux réalisations \(N^{(\lambda+h)}\) et \(N^{(\lambda-h)}\) en utilisant la méthode de l’inverse de la fonction de répartition. Dans ce deuxième estimateur, les lois log-normales sont indépendantes. On a donc
où pour \(k \ge 1\), \(S^{(\lambda+h)}_k = \sum_{i = 1}^{G(\lambda+h, U_k)} X_{i,k}\) et \(\bar S^{(\lambda-h)}_k = \sum_{i = 1}^{G(\lambda-h, U_k)} \bar X_{i,k}\) avec \(G(\lambda, u)\) l’inverse généralisée de la loi de Poisson de paramètre \(\lambda\), \((U_k)_{k \ge 1}\) suite i.i.d. uniforme sur \([0,1]\) indépendante de \((X_{i,k})_{i\ge1, k\ge 1}\) et \((\bar X_{i,k})_{i\ge1, k\ge 1}\) deux suites (doublement indicées) i.i.d. de loi log-normale (de paramètres \(\mu\) et \(\sigma\) inchangés).
Un troisième estimateur \(J^{(3)}_{n,h}(\lambda)\) utilise des réalisations fortements corrélées de la loi de Poisson et des variables aléatoires log-normales communes.
où pour \(k \ge 1\), \(S^{(\lambda+h)}_k = \sum_{i = 1}^{G(\lambda+h, U_k)} X_{i,k}\) et \(S^{(\lambda-h)}_k = \sum_{i = 1}^{G(\lambda-h, U_k)} X_{i,k}\) avec \(G(\lambda, u)\) l’inverse généralisée de la loi de Poisson de paramètre \(\lambda\), \((U_k)_{k \ge 1}\) suite i.i.d. uniforme sur \([0,1]\) indépendante de \((X_{i,k})_{i\ge1, k\ge 1}\) une suite (doublement indicée) i.i.d. de loi log-normale.
4.5.2. Question: plusieurs estimateurs des différences finies#
On fixe les paramètres \(\lambda = 10\), \(\mu = 0.1\), \(\sigma = 0.3\) et \(K = 20\). Programmer ces 3 estimateurs pour différentes valeurs de \(h\) (par exemple, \(h=1\), 0.5, 0.1 et 0.01), et donner le résultat des estimateurs Monte Carlo avec \(n = 50\,000\).
Que se passe-t-il lorsque \(h\) tend vers 0? Comparez le comportement pour ces 3 estimateurs. Il est très important de bien interpréter ces tableaux de résultats et de conclure qu’il faut utiliser l’estimateur \(J^{(3)}_{n, h}(\lambda)\) et en aucun cas l’estimateur \(J^{(1)}_{n,h}(\lambda)\).
Remarque: on considère ici uniquement l’étude de l’erreur statistique dûe à la méthode de Monte Carlo. On ne considère pas l’erreur de biais qui décroît lorsque \(h\) tend vers 0 et qui est peut-être non négligeable pour \(h = 1\). Les IC construits ici sont biaisés et on ne peut pas affirmer que la vraie valeur est dans l’IC à 95% (au moins pour les grandes valeurs de \(h\)).
lambd, mu, sigma = 10, 0.1, 0.3
K = 20
def J1(n, h):
sample_Sph = simu_S(n, mu, sigma, lambd+h)
sample_Smh = simu_S(n, mu, sigma, lambd-h)
xph = (sample_Sph > K).astype(int)
xmh = (sample_Smh > K).astype(int)
return monte_carlo((xph - xmh)/(2*h))
# on crée une fonction pour ne pas répéter ces lignes de code
def result_estimator(J, n=50000, hs=[1, 0.5, 0.1, 0.01]):
result = [ J(n, h) for h in hs ]
df = pd.DataFrame(result,
columns=['mean', 'var', 'lower', 'upper'],
index=hs)
return df
result_estimator(J1)
| mean | var | lower | upper | |
|---|---|---|---|---|
| 1.00 | 0.01753 | 0.012798 | 0.016538 | 0.018522 |
| 0.50 | 0.01652 | 0.044648 | 0.014668 | 0.018372 |
| 0.10 | 0.01080 | 1.003903 | 0.002018 | 0.019582 |
| 0.01 | 0.01700 | 104.051792 | -0.072410 | 0.106410 |
def J2(n, h):
sample_U = rng.random(size=n)
sample_Nph = stats.poisson(mu = lambd+h).ppf(sample_U)
sample_Nmh = stats.poisson(mu = lambd-h).ppf(sample_U)
sample_Sph = np.empty(n)
sample_Smh = np.empty(n)
for k, (Nph, Nmh) in enumerate(zip(sample_Nph, sample_Nmh)):
sample_Sph[k] = np.sum(rng.lognormal(size=int(Nph), mean=mu, sigma = sigma))
sample_Smh[k] = np.sum(rng.lognormal(size=int(Nmh), mean=mu, sigma = sigma))
xph = (sample_Sph > K).astype(int)
xmh = (sample_Smh > K).astype(int)
return monte_carlo((xph - xmh)/(2*h))
result_estimator(J2)
| mean | var | lower | upper | |
|---|---|---|---|---|
| 1.00 | 0.01668 | 0.008572 | 0.015868 | 0.017492 |
| 0.50 | 0.01730 | 0.024041 | 0.015941 | 0.018659 |
| 0.10 | 0.01150 | 0.467377 | 0.005508 | 0.017492 |
| 0.01 | -0.02700 | 42.450120 | -0.084109 | 0.030109 |
def J3(n, h):
sample_U = rng.random(size=n)
sample_Nph = stats.poisson(mu = lambd+h).ppf(sample_U).astype(int)
sample_Nmh = stats.poisson(mu = lambd-h).ppf(sample_U).astype(int)
sample_Sph = np.empty(n)
sample_Smh = np.empty(n)
for k, (Nph, Nmh) in enumerate(zip(sample_Nph, sample_Nmh)):
max_N = max(Nph, Nmh)
sample_X = rng.lognormal(size=max_N, mean=mu, sigma = sigma)
sample_Sph[k] = np.sum(sample_X[:Nph])
sample_Smh[k] = np.sum(sample_X[:Nmh])
xph = (sample_Sph > K).astype(int)
xmh = (sample_Smh > K).astype(int)
return monte_carlo((xph - xmh)/(2*h))
result_estimator(J3)
| mean | var | lower | upper | |
|---|---|---|---|---|
| 1.00 | 0.01699 | 0.008207 | 0.016196 | 0.017784 |
| 0.50 | 0.01706 | 0.016769 | 0.015925 | 0.018195 |
| 0.10 | 0.01560 | 0.077758 | 0.013156 | 0.018044 |
| 0.01 | 0.01900 | 0.949658 | 0.010458 | 0.027542 |
