Algorithme de Metropolis et du recuit simulé

5. Algorithme de Metropolis et du recuit simulé#

Dans une première partie, on utilise l’algorithme de Metropolis pour construire une chaine de Markov de probabilité invariante $\mu$ donnée.

Dans une deuxième partie, on implémente l’algorithme du recuit simulé pour optimiser une fonction sur un espace discret grand. Le problème d’optimisation considéré est celui du “voyageur de commerce” qui est un problème classique en optimisation discrète.

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme() 
from numpy.random import default_rng
rng = default_rng()

5.1. Algorithme de Metropolis#

Soit $E$ un ensemble dénombrable et $\mu$ une probabilité sur $E$. L’algorithme de Metropolis permet de construire une chaîne de Markov de probabilité invariante $\mu$.

Soit $P$ une matrice stochastique, dite de sélection (ou de proposition), qui permet de parcourir l’espace d’état $E$ et $\rho$ la fonction définie par

\[ \forall x, y \in E, \quad \rho(x, y) = \frac{\mu(y) P(y, x)}{\mu(x) P(x, y)} \wedge 1. \]

On considère la matrice stochastique

\[\begin{split} Q(x, y) = \begin{cases} P(x, y) \rho(x, y) & \text{si $x \neq y$} \\ 1 - \sum_{z \neq x} Q(x, z) & \text{si $x = y$}. \end{cases} \end{split}\]

Alors sous les hypothèses adhoc, la chaine de Markov $(Y_n)_{n \ge 1}$ de transition $Q$ a pour unique probabilité invariante $\mu$ et $(Y_n)_{n \ge 1}$ converge en loi vers $\mu$.

5.2. Petit exemple sur $\mathbf{Z}$#

On considère la probabilité $\mu$ sur $E = \mathbf{Z}$ définie par

\[ \forall x \in \mathbf{Z}, \quad \mu(x) = C \exp \bigl(-\frac{|x|}{5}\bigr). \]

Soit $P$ la matrice de transition de la marche aléatoire symmétrique sur $\mathbf{Z}$ définie par $P(x, x-1) = P(x, x+1) = \frac{1}{2}$.

5.2.1. Question: simulation de la chaine de transition $Q$#

Ecrire la dynamique de la chaine $(Y_n)_{n \ge 0}$ de matrice de transition $Q$ (et de loi invariante $\mu$).
Coder cette dynamique dans une fonction phi de sorte que l’appel suivant crée un échantillon de $1\,000$ trajectoires sur $\{0, \dots, 100\}$.

5.2.2. Question: trajectoires et histogramme#

Visualiser quelques trajectoires de $(Y_n)_{n=0,\dots,1000}$ et comparer l’histogramme à l’itération 1000 avec la densité $\mu$.

5.3. Algorithme du recuit simulé#

Soit $E$ fini et $H:E \to \mathbf{R}$ une fonction dont on cherche un minimum. On considère une mesure de Gibbs paramétrée par $T > 0$ de la forme

\[ \mu_T(x) = \frac{1}{Z_T} \exp \bigl(- \frac{H(x)}{T} \bigr), \]

où $Z_T$ est la constante de normalisation souvent appelée fonction de partition. Lorsque $T$ tend vers $0$ la mesure $\mu_T$ se concentre sur l’ensemble des minimums de $H$, on considère donc une suite déterministe $(T_n)_{n \ge 1}$ qui tend vers 0 et l’algorithme de Metropolis (inhomogène) suivant:

\[\begin{split} Q_n(x, y) = \begin{cases} P(x, y) \exp \Bigl( - \frac{(H(y) - H(x))_+}{T_n} \Bigr) & \text{si $x \neq y$} \\ 1 - \sum_{z \neq x} Q_n(x, z) & \text{si $x = y$}. \end{cases} \end{split}\]

où $P$ est une matrice stochastique irréductible symétrique.

5.4. Problème du voyageur de commerce#

L’énoncé du problème du voyageur de commerce est le suivant : étant donné $N$ points (des « villes ») et les distances séparant chaque point, trouver un chemin de longueur totale minimale qui passe exactement une fois par chaque point et revienne au point de départ. La distance considérée ici est la distance euclidienne.

Soit $N$ villes fixées représentées par un vecteur $V = (V_1, \dots, V_N) \in ([0,1]^2)^N$. Une composante de ce vecteur $V$ est la coordonnée d’une ville dans $[0,1]^2$ et la distance euclidienne $d$ entre 2 villes $V_i$ et $V_j$ est notée dans la suite $d(V_i, V_j)$. Un trajet est identifié par une permutation de $\{1,\dots,N\}$.

Ainsi $E = \mathcal{S}_N$ l’ensemble des permutations de $\{1,\dots,N\}$ et $H$ que l’on appelle ici la longueur d’un trajet $x \in E$ est définie par

\[ \forall x \in E, \quad H(x) = \sum_{i=1}^{N-1} d \bigl(V_{x_i}, V_{x_{i+1}} \bigr) + d \bigl(V_{x_N}, V_{x_{1}} \bigr) \]

Pour information il y a $\operatorname{Card}\big(H(E)\big) = \frac{N !}{2 N}$ longueurs de trajets possibles.

5.4.1. Question: chargement des données#

En python on peut accéder en lecture à un fichier texte en utilisant la fonction open qui crée un objet que l’on peut interoger (parcourir) pour lire le contenu du fichier. La méthode readlines d’un tel objet crée une liste donc chaque élément est une chaine de caractère. Par exemple la cellule suivante renvoie les 4 premières lignes du fichier 'data/villes.csv'.

file = open('data/villes.csv', mode = 'r')
lines = file.readlines()
file.close()
lines[:4]

[' x, y\n',
 '0.509881702484563, 0.323756906203926\n',
 '0.304272808600217, 0.0117385489866138\n',
 '0.564815347781405, 0.434346224879846\n']

En utilisant les méthodes split et strip des chaines de caractères créer un np.array villes contenants les coordonnées des 30 villes du fichier data/villes.csv. Le np.array doit donc avoir 30 lignes et 2 colonnes et être composé de réels (float64).

Alternative: utiliser la fonction read_csv du module pandas.

5.4.2. Question: préparatifs#

Définir une fonction distance(v1, v2) qui calcule la distance euclidienne entre 2 villes (2 lignes de la matrice villes).
Définir une fonction H(x) qui à une configuration $x \in E$ (une permutation de $\{1,\dots,n\}$) renvoie la longueur du trajet (longueur totale en revenant au point de départ).
Définir une fonction plot_path(x, ax) qui affiche le chemin de la configuration x dans l’objet ax de type Axes. Par exemple pour la configuration initiale x = np.arange(N) vous devez obtenir ce tracé: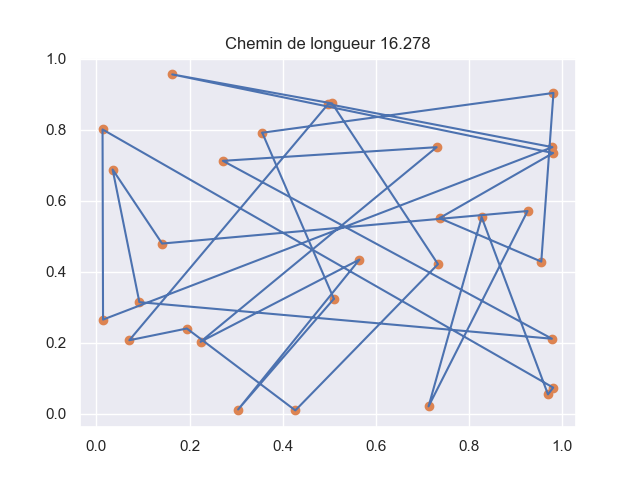

Pour mettre en oeuvre l’algorithme de recuit simulé il faut choisir une matrice de proposition $P$ pour parcourir l’espace et une suite $(T_n)_{n \ge 1}$ qui tend vers 0. Dans la suite on définit la fonction de température $T$ par $$ \forall n \ge 1, \quad T(n) = \frac{0.01}{\log(n+1)} $$

def T(n): 
    return 0.01 / np.log(n+1)

5.4.3. Question: première matrice de proposition $P_1$#

La première matrice de transition que l’on considère pour explorer l’espace des configurations $E = \mathcal{S}_n$ est la plus intuitive. Etant donné un trajet $x \in E$ on tire 2 indices $i$ et $j$ de $\{1,\dots,N\}$ et on échange ces indices c’est à dire qu’on propose le trajet voisin $y$ défini si $i < j$ (par exemple) par $$ y = (x_1, \dots, x_{i-1}, x_{j}, x_{i+1}, \dots, x_{j-1}, x_{i}, x_{j+1}, \dots, x_N) $$

Définir une fonction phi_P1 qui code la dynamique basée sur cette proposition. La fonction prend un argument x et renvoie un trajet voisin y.

Attention: l’argument x ne doit pas être modifié. Tester votre fonction.

5.4.4. Question: algorithme du recuit simulé#

Définir une fonction phi_Q(phi_P, T, xn, n) qui construit le prochain état de la chaine de Markov de transition $Q_n$ sachant qu’on est dans l’état $x_n$ à l’itération $n$.

Ecrire une fonction

recuit_simule(phi_P, T=T, x0=np.arange(N), n_iters=3000)

qui applique l’algorithme du recuit simulé sur n_iters itérations et renvoie le dernier trajet obtenu et la liste de toutes les longueurs obtenues de 0 à n_iters.

Tracer le chemin et le graphe des longueurs en fonction de $n$. Répliquer plusieurs fois pour obtenir différents résultats (assez variables).

5.4.5. Question: variantes sur la matrice de sélection#

La première variante consiste à supprimer le cas où l’on propose en $n+1$ un trajet similaire à celui en $n$. C’est le cas avec la matrice $P_1$ car $P_1(x, x) = \frac{1}{N} > 0$. Pour cela il suffit de tirer 2 indices $i$ et $j$ de $\{1,\dots,N\}$ sans remise, et on aura donc $i \neq j$.
La seconde variante consiste à partir de 2 indices $i$ et $j$ différents de couper le trajet en ces indices et de retourner le trajet entre ces 2 indices. Ainsi le trajet voisin proposé $y$ à partir de $x$ est défini par $$ y = (x_1, \dots, x_{i-1}, x_{j}, x_{j-11}, \dots, x_{i+1}, x_{i}, x_{j+1}, \dots, x_N) $$

Coder les fonctions phi_P2 et phi_P3 similaires à phi_P1 qui correspondent aux variantes proposées ci-dessus.

5.4.6. Question: résultats avec ces matrices de proposition#

Appliquer l’algorithme de recuit simulé pour chaque stratégie d’exploration proposée. Répliquer plusieurs fois pour obtenir différents résultats.

5.4.7. Question: extensions#

Lire le fichier data/best.csv qui contient la configuration x optimale, c’est à dire de longueur minimale (sauf si vous trouvez mieux!). Tracer ce chemin.
Attention: les villes sont numérotées de 1 à N dans le fichier…

Quelque suggestions pour aller plus loin:

Reprendre les questions précédentes en faisant varier la fonction de température.
Modifier votre code pour construire simultanément $M$ réalisations indépendantes de l’algorithme du recuit simulé.
Donner la répartition empirique sur $M$ trajectoires des longueurs trouvées pour chaque matrice de proposition $P_1$, $P_2$ et $P_3$.