1  Simulation exacte de processus

1.1 Simulation en NumPy et SciPy

import numpy as np 
import scipy.stats as sps 
import matplotlib.pyplot as plt
import seaborn as sns 
sns.set_theme()

1.1.1 Module random de NumPy

Le sous-module random de NumPy est utilisé pour générer des nombres pseudo-aléatoires et des échantillons à partir de distributions statistiques communes (normal, uniforme, poisson, etc.).

Important

Le sous-module random de NumPy a subi une refonte significative dans ses versions récentes. La version 1.17 (2019) introduit un nouveau mécanisme pour la génération de nombres pseudo-aléatoires. Ce mécanisme repose sur un objet appelé Generator, remplaçant les fonctions globales antérieures de NumPy (le contexte globale était appelé RandomState). Plutôt que d’appeler directement des fonctions globales comme np.random.normal ou np.random.uniform, il est maintenant préférable d’instancier un objet Generator, et d’appeler ses méthodes pour générer des réalisations de variables aléatoires.

Il est recommandé de lire la documentation officielle. Par défaut l’algorithme utilisé pour les nombres pseudo-aléatoires est le PCG64.

Voici un exemple d’utilisation de ce mécanisme basé sur l’objet Generator.

from numpy.random import default_rng, SeedSequence

sq = SeedSequence()
seed = sq.entropy        # on sauve la graine pour reproduire les résultats
rng = default_rng(sq)
rng.standard_normal(5)

array([ 0.22064422, -1.92880041, -1.20913725, -0.35320863,  0.58424854])

Dans le code précédent:

• l’objet SeedSequence crée une séquence de graine qui produit une graine de manière déterministe ou aléatoire. Sans paramètre, SeedSequence() utilise l’état aléatoire global de la machine pour générer une graine.
• rng est un objet Generator qui produit des nombres pseudo-aléatoires selon l’algorithme PCG64,
• on obtient 5 réalisations de la Gaussienne (centrée réduite) par des transformations des nombres pseudo-aléatoires. La transformation utilisée n’est pas l’algorithme de Box-Muller mais une méthode de rejet appelée Ziggurat.

Pour reproduire les résultats, on initialise un nouvel objet rng2 avec la graine sauvegardée.

rng2 = default_rng(seed)
rng2.standard_normal(10)

array([ 0.22064422, -1.92880041, -1.20913725, -0.35320863,  0.58424854,
        1.31354339,  0.36239927,  0.84219083,  1.10597482,  0.78862674])

Note

L’objet SeedSequence permet aussi d’initialiser plusieurs Generator considérés comme indépendants: c’est important pour écrire un code parallèle (multithreading).

1.1.2 Module stats de SciPy

Le module scipy.stats utilise une programmation type orientée objet.

La principale utilisation de ce module est la manipulation de variables aléatoires. On initialise un objet via le nom d’une distribution. Puis de cet objet on peut connaitre la densité/masse, la fonction de répartition ou obtenir des réalisations (en fait obtenues généralement via NumPy).

dist_continu = [d for d in dir(sps) if
                isinstance(getattr(sps, d), sps.rv_continuous)]
dist_discrete = [d for d in dir(sps) if
                 isinstance(getattr(sps, d), sps.rv_discrete)]
print("Nombres de distributions à densité: ", len(dist_continu))
print(dist_continu)
print("Nombres de distributions discrètes: ", len(dist_discrete))
print(dist_discrete)

Nombres de distributions à densité:  110
['alpha', 'anglit', 'arcsine', 'argus', 'beta', 'betaprime', 'bradford', 'burr', 'burr12', 'cauchy', 'chi', 'chi2', 'cosine', 'crystalball', 'dgamma', 'dpareto_lognorm', 'dweibull', 'erlang', 'expon', 'exponnorm', 'exponpow', 'exponweib', 'f', 'fatiguelife', 'fisk', 'foldcauchy', 'foldnorm', 'gamma', 'gausshyper', 'genexpon', 'genextreme', 'gengamma', 'genhalflogistic', 'genhyperbolic', 'geninvgauss', 'genlogistic', 'gennorm', 'genpareto', 'gibrat', 'gompertz', 'gumbel_l', 'gumbel_r', 'halfcauchy', 'halfgennorm', 'halflogistic', 'halfnorm', 'hypsecant', 'invgamma', 'invgauss', 'invweibull', 'irwinhall', 'jf_skew_t', 'johnsonsb', 'johnsonsu', 'kappa3', 'kappa4', 'ksone', 'kstwo', 'kstwobign', 'landau', 'laplace', 'laplace_asymmetric', 'levy', 'levy_l', 'levy_stable', 'loggamma', 'logistic', 'loglaplace', 'lognorm', 'loguniform', 'lomax', 'maxwell', 'mielke', 'moyal', 'nakagami', 'ncf', 'nct', 'ncx2', 'norm', 'norminvgauss', 'pareto', 'pearson3', 'powerlaw', 'powerlognorm', 'powernorm', 'rayleigh', 'rdist', 'recipinvgauss', 'reciprocal', 'rel_breitwigner', 'rice', 'semicircular', 'skewcauchy', 'skewnorm', 'studentized_range', 't', 'trapezoid', 'triang', 'truncexpon', 'truncnorm', 'truncpareto', 'truncweibull_min', 'tukeylambda', 'uniform', 'vonmises', 'vonmises_line', 'wald', 'weibull_max', 'weibull_min', 'wrapcauchy']
Nombres de distributions discrètes:  21
['bernoulli', 'betabinom', 'betanbinom', 'binom', 'boltzmann', 'dlaplace', 'geom', 'hypergeom', 'logser', 'nbinom', 'nchypergeom_fisher', 'nchypergeom_wallenius', 'nhypergeom', 'planck', 'poisson', 'poisson_binom', 'randint', 'skellam', 'yulesimon', 'zipf', 'zipfian']

Voici un exemple d’utilisation aver la loi exponentielle (de paramètre \(\lambda = 2\)).

lambd = 2
E = sps.expon(scale = 1./lambd)
E.cdf(1)    # appel de la méthode `cdf` fonction de répartition 

fig, (ax1, ax2) = plt.subplots(ncols=2, nrows=1)
x = np.linspace(E.ppf(0.01), E.ppf(0.99), 100)
ax1.plot(x, E.pdf(x))
ax1.set_title("Densité")
ax2.plot(x, E.cdf(x), color='C1')
ax2.set_title("Fonction de répartition")
fig.suptitle(fr"Loi exponentielle de paramètre $\lambda={lambd}$");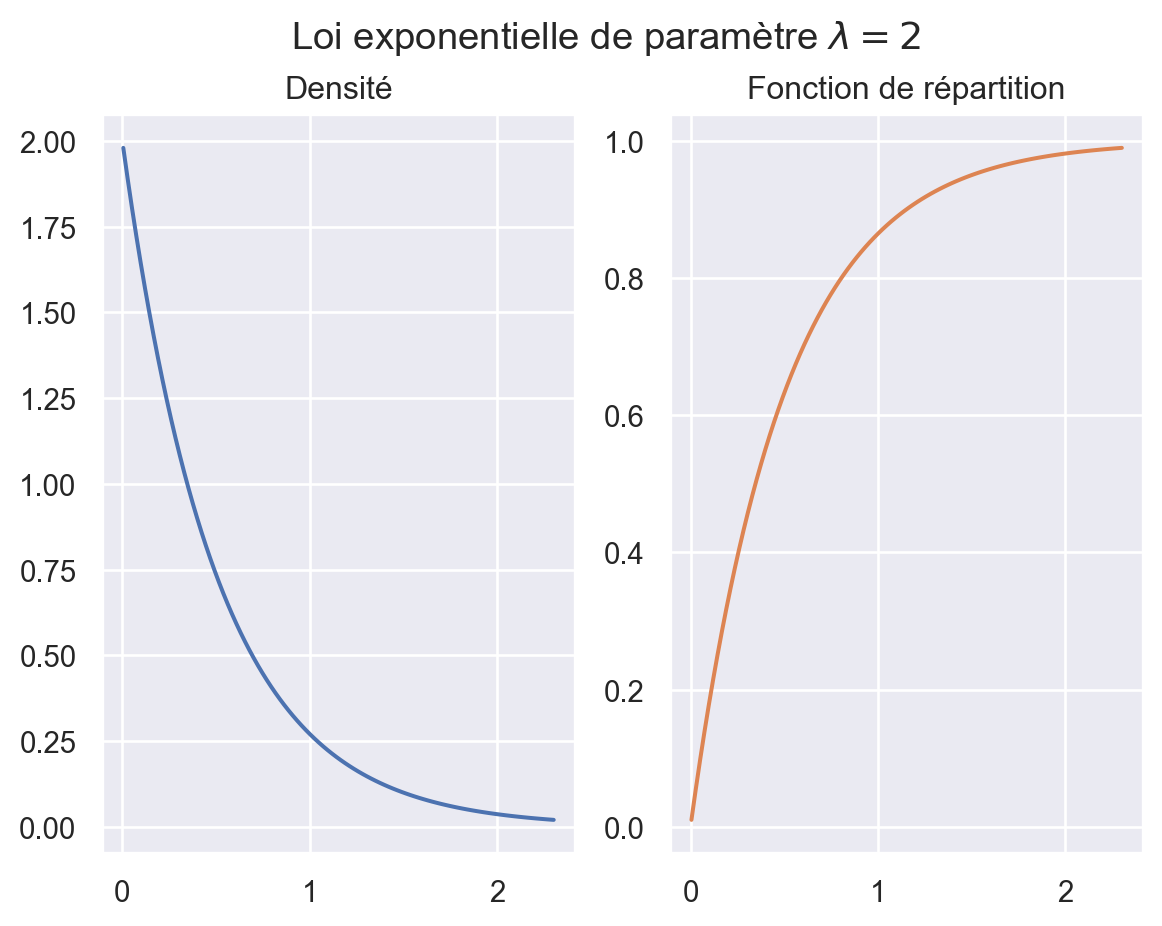

Pour obtenir des réalisations indépendantes de cette variable aléatoire \(E\) on appelle la méthode rvs. Par exemple

E.rvs(size=(3, 5), random_state=rng)

array([[0.56672524, 0.48133581, 0.02650131, 0.2597668 , 0.29751193],
       [0.08898362, 0.2150716 , 0.71466063, 0.17017714, 1.26438832],
       [0.22735664, 0.55058624, 0.37709012, 0.27681425, 0.3650381 ]])

Mise en garde

Pour être cohérent avec la nouvelle approche NumPy il faut passer l’objet rng notre générateur de nombres pseudo-aléatoires comme argument à la méthode rvs.

1.2 Mouvement Brownien

Le mouvement Brownien est l’une des briques de base pour la construction de processus à temps continu. Une autre brique de base est le processus de Poisson pour prendre en compte d’éventuelle discontinuité. Pour ces processus il est possible de faire de la simulation exacte, c’est à dire sans erreur de discrétisation.

Note

La simulation exacte d’un processus \((X_t)_{t \in [0,T]}\) consiste en la simulation du vecteur aléatoire \((X_{t_0}, \dots, X_{t_N})\) pour des instants donnés \(0 = t_0 \le \cdots \le t_N = T\). Souvent on découpe l’intervalle \([0, T]\) en \(N\) intervalles de même longueur c’est à dire en considérant \(N+1\) points \(t_k\) définis par \[t_k = k \frac{T}{N} \quad \forall k \in \{0,\dots,N\}.\]

1.2.1 Mouvement Brownien Standard (Dimension 1)

On rappelle deux définitions possibles (et équivalentes) d’un mouvement Brownien standard \((B_t)_{t \ge 0}\).

1. \((B_t)_{t \ge 0}\) est un PAIS (Processus à Accroissements Indépendants et Stationnaires), à trajectoires continues p.s., nul en 0, tel que \(B_t \sim \mathcal{N}(0,t)\).
2. \((B_t)_{t \ge 0}\) est un processus gaussien, à trajectoires continues p.s., nul en 0, et de fonction de covariance \(\gamma(s, t) = \mathrm{Cov}(B_s, B_t) = \mathbf{E}[B_s B_t] = s \wedge t\).

Important

Exercice: Ecrire l’algorithme de simulation de \((B_0, \dots, B_{t_N})\) en utilisant la définition 1. puis la défintion 2. et faire le lien.

1.2.1.1 Simulation en tant que PAIS

D’après la définition 1. on simule d’abord les accroissements indépendants \[ B_{t_{k+1}} - B_{t_k} \sim \mathcal{N}(0, t_{k+1}-t_{k}) \] puis on reconstruit \(B_{t_k} = \displaystyle \sum_{j=0}^{k-1} (B_{t_{j+1}} - B_{t_j})\) (somme téléscopique).

A partir de \(N\) gaussiennes indépendantes \((G_k)_{k=1,\dots,N}\) on construit le vecteur \((B_{t_1},\dots,B_{t_N})\) par la récurrence: \[ B_{t_{k+1}} = B_{t_k} + \sqrt{t_{k+1} - t_k} G_{k+1}. \]

Mise en garde

Pour simuler \(M\) trajectoires il faut \(M \times N\) réalisations indépendantes de gaussiennes. En NumPy, dans la mesure du possible, il faut tout simuler d’un bloc (un seul appel de rng.standard_normal) et mettre en mémoire les \(M \times N\) données.

def brownian_1d(n_paths: int,
                times: np.ndarray,
                increments: bool = False, 
                rng: np.random.Generator = None) -> np.ndarray:
    """
    Simule des trajectoires de mouvement brownien standard en 1D.

    Args:
        n_paths: Nombre de trajectoires à simuler.
        times: tableau 1d (list, tuple ou np.ndarray) de taille `n_times` 
               qui contient les instants $t_k$.
        increments: Si `True`, les accroissements sont retournés, 
                    sinon ce sont les trajectoires.
        rng: objet `Generator`, création si `None` (non recommandé).

    Returns:
        - si `increments=False`: np.ndarray de forme `(n_paths, n_times)` 
          contenant les trajectoires aux instants $t_k$.
        - si `increments=True`: np.ndarray de forme `(n_paths, n_times-1)`
          contenant les accroissements entre les instants $t_k$.
    """
    # Initialisation du générateur pseudo-aléatoire si non fourni
    if rng is None:
        rng = np.random.default_rng()

    # Calcul des accroissements (utilisation du broadcasting)
    dt = np.diff(times)
    dB = np.sqrt(dt) * rng.standard_normal((n_paths, len(dt)))

    # Si les accroissements sont demandés
    if increments:
        return dB

    # Construction des trajectoires browniennes (cumul des incréments)
    paths = np.hstack([np.zeros((n_paths,1)), np.cumsum(dB, axis=1)])
    return paths

Voici un code illustrant l’utilisation de cette fonction.

N, M = 100, 200
T = 1
times = np.arange(N+1)*(T / N)
paths = brownian_1d(M, times, rng=rng)

fig, ax = plt.subplots()
for path in paths:
    ax.plot(times, path, color='C0', alpha=0.3)
ax.plot(times, paths[0,:], color='C1', lw=2, label='One path')
ax.legend()
ax.set_title(f"{M} standard Brownian motion paths with N={N}");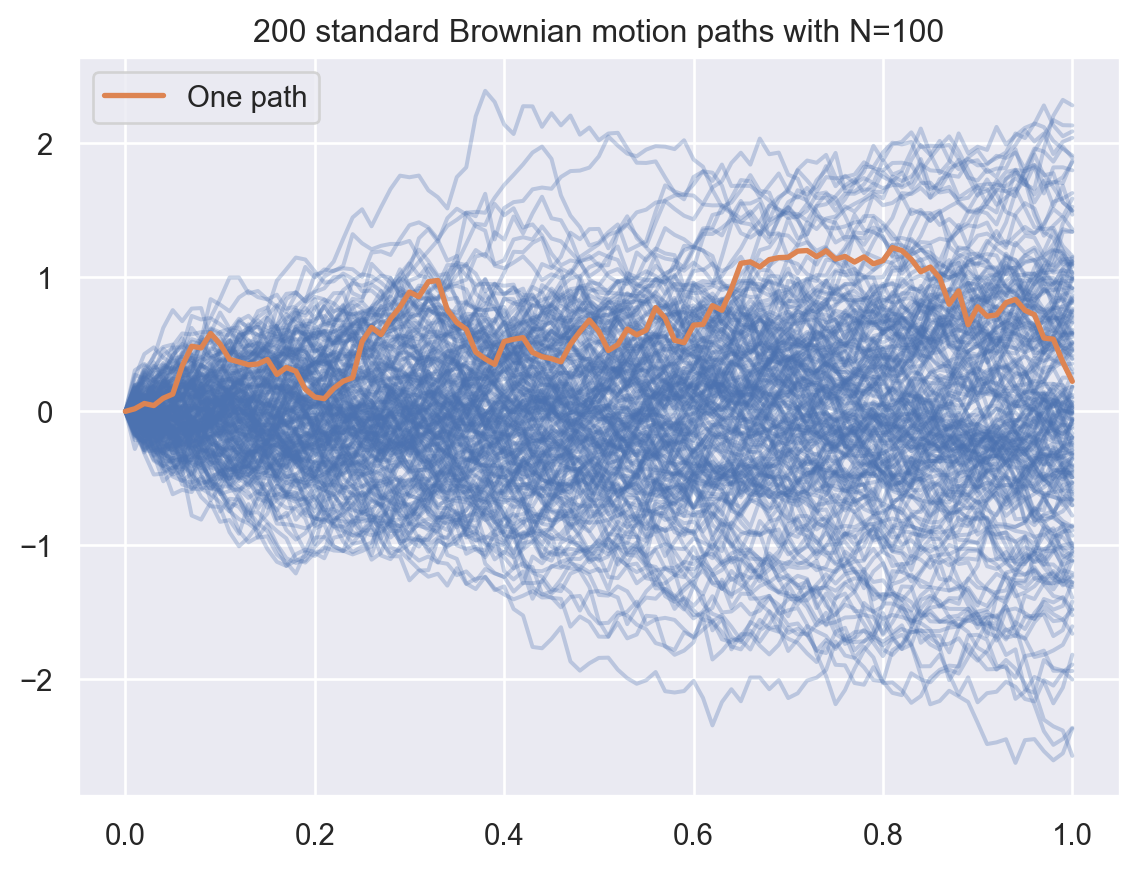

1.2.1.2 Simulation en temps que processus gaussien

D’après la définition 2. on a \[ \begin{pmatrix} B_{t_1} \\ \vdots \\ B_{t_N} \end{pmatrix} \sim \mathcal{N} \big(0, \Sigma \big), \quad \text{avec} \quad \Sigma = \begin{pmatrix} t_1 & t_1 & \cdots & t_1 & t_1 \\ t_1 & t_2 & \cdots & t_2 & t_2 \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ t_1 & t_2 & \cdots & t_{N-1} & t_{N-1} \\ t_1 & t_2 & \cdots & t_{N-1} & t_N \end{pmatrix}. \]

La matrice \(\Sigma\) est symétrique définie positive donc par la décomposition de Cholesky il existe une matrice triangulaire inférieure \(L\) telle que \(L L^\top = \Sigma\). Ainsi le vecteur \((B_{t_1}, \dots, B_{t_N})\) a même loi que \(L G\) où \(G = (G_1, \dots, G_n) \sim \mathcal{N}(0, \operatorname{Id}_N)\).

Note

Pour tout vecteur aléatoire \(X \in \mathbf{L}^2(\mathbf{R}^d)\), et toute matrice \(A \in \mathcal{M}(q, d)\), le vecteur \(Y = AX \in \mathbf{L}^2(\mathbf{R}^q)\) et la matrice de covariance du vecteur \(Y\) est donnée par \(C_Y = A C_X A^\top\) où \(C_X\) est la matrice de covariance du vecteur \(X\).

def gaussian_process_1d(n_paths: int,
                        times: np.ndarray,
                        means: np.ndarray, 
                        covariances: np.ndarray,
                        rng: np.random.Generator = None) -> np.ndarray:
    """
    Simule des trajectoires de mouvement brownien standard en 1D.

    Args:
        n_paths: Nombre de trajectoires à simuler.
        times: Tableau 1d (list, tuple ou np.ndarray) de taille `n_times` 
               qui contient les instants $t_k$.
        means: Tableau 1d (list, tuple ou np.ndarray) de taille `n_times` 
               qui contient les moyennes aux instants $t_k$.
        covariances: `np.ndarray` de forme `(n_times-1, n_times-1)` 
               qui contient les covariances  
        rng: objet `Generator`, création si `None` (non recommandé).

    Returns:
        np.ndarray de forme `(n_paths, n_times)` contenant les trajectoires 
        aux instants $t_k$ du processus gaussien.
    """
    # Initialisation du générateur pseudo-aléatoire si non fourni
    if rng is None:
        rng = np.random.default_rng()

    L = np.linalg.cholesky(covariances)
    G = rng.standard_normal((n_paths, len(times)-1))
    B = np.einsum('ij,pj->pi', L, G)
    # ou bien B = (L @ G.T).T

    paths = means + np.hstack([np.zeros((n_paths,1)), B])
    return paths

N, M = 100, 200
T = 1
times = np.arange(N+1)*(T / N)
Sigma = np.minimum(times[1:], times[1:,np.newaxis])

paths = gaussian_process_1d(M, times, 
                            means = np.zeros_like(times), 
                            covariances = Sigma, 
                            rng = rng)

fig, ax = plt.subplots()
for path in paths:
    ax.plot(times, path, color='C0', alpha=0.3)
ax.plot(times, paths[0,:], color='C1', lw=2, label='One path')
ax.legend()
ax.set_title(f"{M} standard Brownian motion paths with N={N}");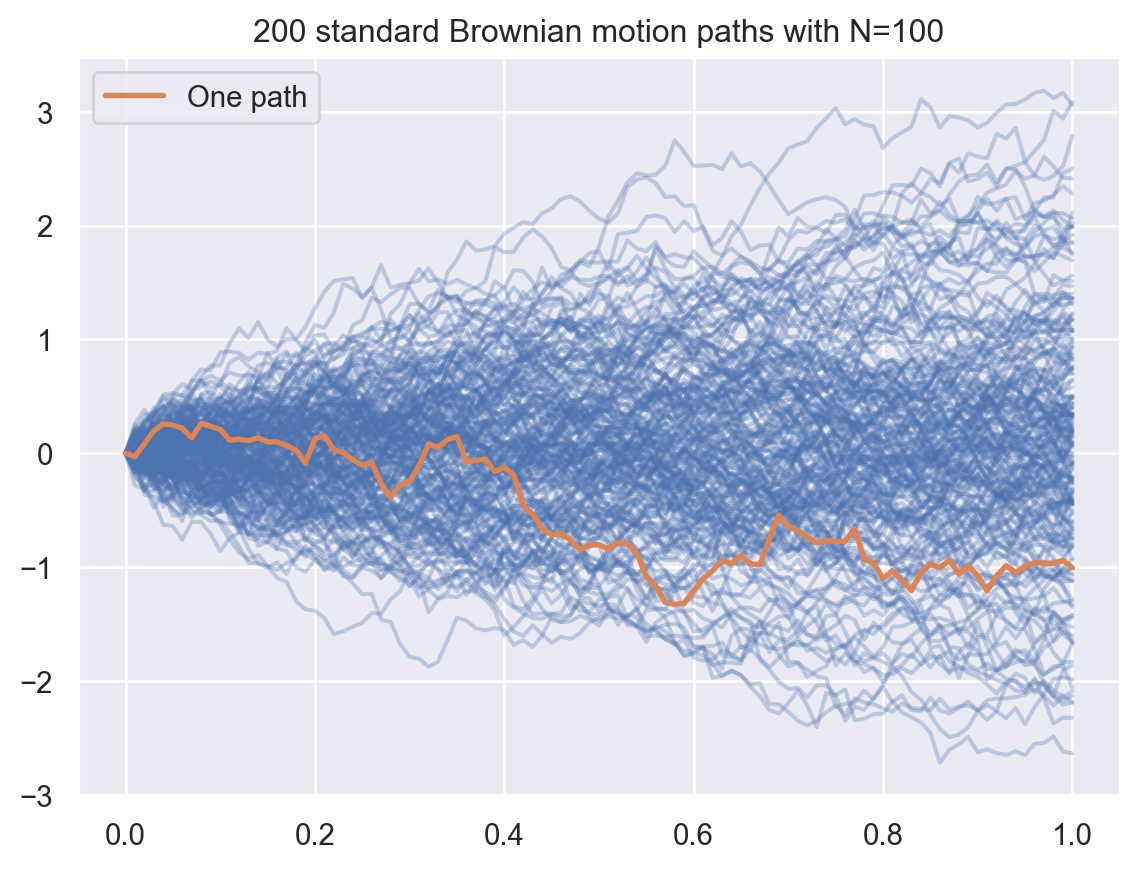

1.2.1.3 Construction récursive

La construction trajectorielle de Paul Lévy permet aussi de simuler le mouvement Brownien: il s’agit d’affiner la trajectoire, itération après itération, en suivant le découpage dyadique de \([0,1]\). Pour cela il faut déterminer la loi conditionnelle du Brownien à l’instant \(t\) sachant ses positions \(x\) et \(y\) respectivement en des instants \(l\) et \(r\) tels que \(l < t < r\).

La propriété principale est la suivante \(\forall l < t < r\), \(\forall x, y \in\mathbf{R}\), \[ B_t \big\lvert \{B_l = x, B_r = y \} \sim \mathcal{N}\left(\frac{r-t}{r-l} x + \frac{t-l}{r-l} y, \frac{(r-t)(t-l)}{r-l} \right). \] En particulier si on considère un temps \(t = \frac{l+r}{2}\) (milieu de \([l,r]\)) alors \(\forall x, y \in\mathbf{R}\), \[ B_{\frac{l+r}{2}} \big\lvert \{B_l = x, B_r = y \} \sim \mathcal{N}\left(\frac{x+y}{2}, \frac{r-l}{4} \right). \]

Soit \((G_{k,n}, 0 \le k < 2^n, n \ge 0)\) une suite (doublement indicée) i.i.d. de loi \(\mathcal{N}(0,1)\). On introduit les instants dyadiques de \([0,1]\) par la notation \(t_k^n = \frac{k}{2^n}\) (on a alors \(t^{n+1}_{2k+1} = \frac{1}{2} (t^n_k + t^n_{k+1})\) les nouveaux instants qui apparaissent à l’échelle \(n+1\)). On définit une suite de processus \((X^n_t)_{t \in [0,1]}\) où pour \(n\) fixé \((t \mapsto X^n_t)\) est linéaire sur chaque intervalle \([t^n_k, t^n_{k+1}[\), et aux points \(t_k^n\): \[ \begin{cases} X^0_0 = 0, \quad \text{et} \quad X^0_1 = G_{0,0}, \\ X^{n+1}_{t^n_k} = X^n_{t^n_k}, \quad \text{et} \quad X^{n+1}_{t^{n+1}_{2k+1}} = X^{n}_{t^{n+1}_{2k+1}} + 2^{-\frac{n}{2}-1} G_{2k+1, n+1}. \end{cases} \] Noter que \(X^n_{t^{n+1}_{2k+1}} = \frac{1}{2} \big(X^n_{t^n_k} + X^n_{t^n_{k+1}}\big)\) par la construction linéaire par morceaux.

Note

• Montrer que le vecteur \((X^n_{t^n_k})_{k =0, \dots, 2^n}\) est Gaussien centré et tel que \(\mathbf{E}\big[X^n_{t^n_k} X^n_{t^n_j}\big] = t^n_k \wedge t^n_j\).
• En déduire que pour \(n \ge 0\) fixé, le processus \((X^n_t)_{t \in [0,1]}\) est à trajectoires continues, Gaussien centré et vérifiant \[ \forall s, t \in [0,1], \quad \mathbf{E}\big[ X^n_s X^n_t \big] = s \wedge t + \mathcal{O}(2^{-n}). \]
• Montrer qu’il existe \(C > 0\) telle que pour tout \(n \ge 0\) \[ \mathbf{P}\big(\sup_{t\in[0,1]} |X^{n+1}_t - X^n_t| > 2^{-\frac{n}{4}}\big) \le C 2^{-n} \]
• En déduire l’existence et la nature du processus limite \((X_t)_{t \in [0,1]}\) de la suite \((X^n_t)_{t \in [0,1]}\) lorsque \(n\) tend vers l’infini.

def refine_brownian_1d(times: np.ndarray, paths: np.ndarray, 
                       rng: np.random.Generator=None) -> tuple :
    """ Raffine les trajectoires Browniennes et les instants de temps 
        en doublant la résolution temporelle.
    
    Args:
        times: np.ndarray de taille N qui contient les instants $t_k$.
        paths: np.ndadday de forme (N, M) où 
          - N est le nombre de points temporels 
          - M est le nombre de trajectoires simulées.
        rng: objet `Generator`, création si `None` (non recommandé).

    Returns:
        tuple: 
          - np.ndarray de forme (2*N - 1, ) avec les instants interpolés.
          - np.ndarray de forme (M, 2*N - 1) avec les trajectoires raffinées.
    """
    if rng is None:
        rng = np.random.default_rng()

    M, N = paths.shape
    dt = np.diff(times)

    # Raffinement des instants de temps 
    r_times = np.empty(2*N - 1)
    r_times[0::2] = times  # Copie des instants originaux
    r_times[1::2] = (times[:-1] + times[1:]) / 2  # Interpolation

    # Raffinement des trajectoires 
    r_paths = np.empty((M, 2*N - 1))
    r_paths[:, 0::2] = paths 
    r_paths[:, 1::2] = (paths[:, :-1] + paths[:, 1:]) / 2 \
                       + np.sqrt(dt / 4) * rng.standard_normal((M, N-1))
    
    return r_times, r_paths

t0 = np.array([0, 1])
W0 = brownian_1d(M, t0, rng=rng)

## Exemple d'appel de la fonction
t1, W1 = refine_brownian_1d(t0, W0, rng=rng)

## Création d'un dictionnaire pour les résultats
result = { 
  0: (t0, W0), 
  1: (t1, W1), 
}

## On complète le dictionnaire des résultats 
for n in range(2, 5): 
    result[n] = refine_brownian_1d(*result[n-1], rng=rng)

## On fait un tracé des trajectoires en fonction du niveau de raffinement $n$
fig, axs = plt.subplots(ncols=2, nrows=2, figsize=(8,8), 
                        sharex=True, sharey=True, layout='tight')
for n, ax in enumerate(axs.flat):
    t, paths = result[n+1]
    for path in paths: 
        ax.plot(t, path, color='C0', alpha=0.3)
    ax.plot(t, paths[0], color='C1', lw=2, label=f'One path')
    ax.legend()
    ax.set_title(f'Iteration $n$={n+1}')
fig.suptitle(f'Raffinement des trajectoires en fonction du paramètre $n$');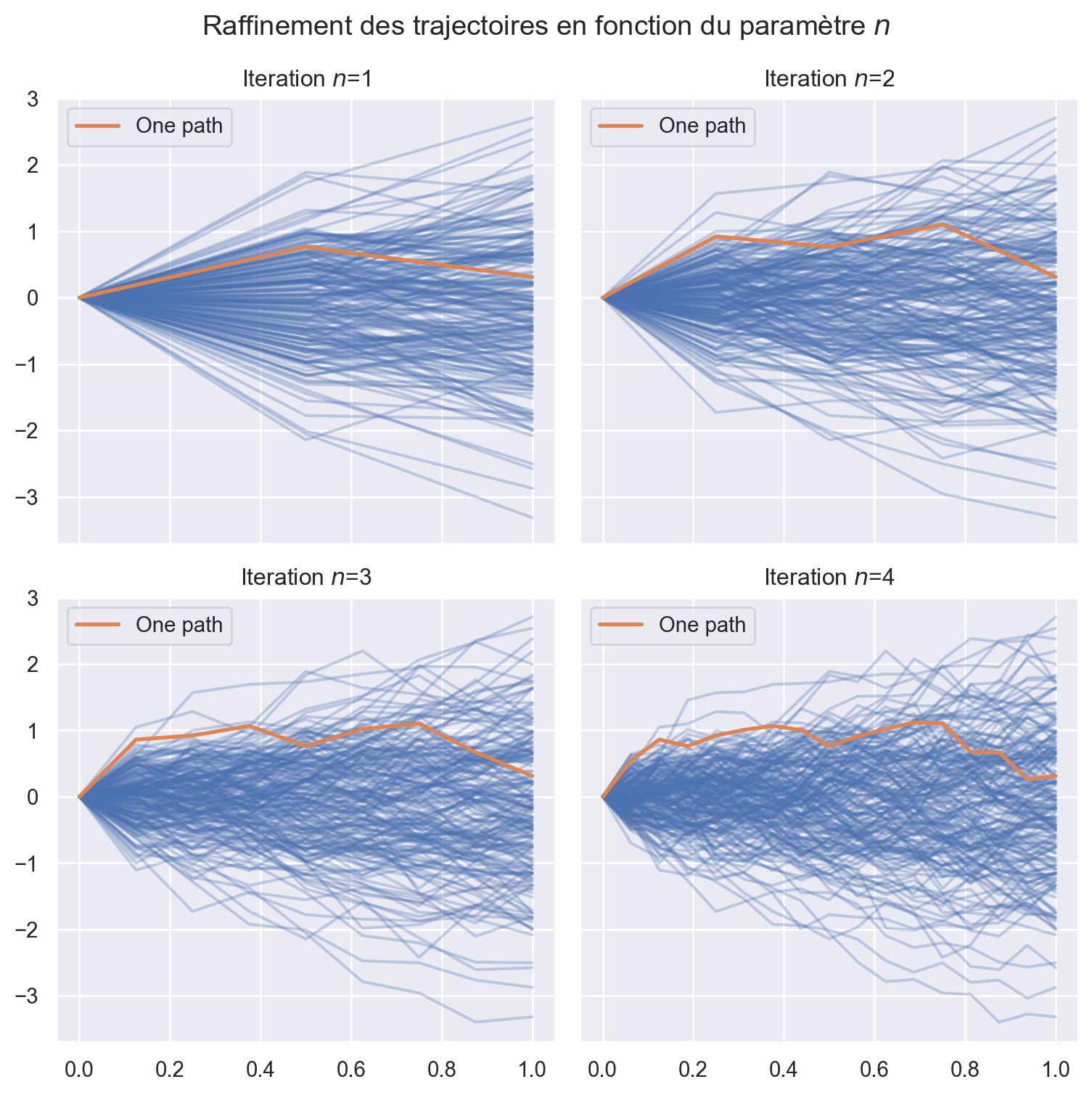

1.2.2 Mouvement Brownien Multidimensionnel

1.2.2.1 Dimension 2

On considère maintenant un mouvement Brownien en dimension 2, \(B = (B^1, B^2)\) de corrélation \(\rho \in [-1,1]\), c’est à dire tel que \(\operatorname{Corr}(B^1_t, B^2_t) = \rho t\). On rappelle que \(B\) se représente sous la forme \[ \begin{cases} B^1_t &= W^1_t, \\ B^2_t &= \rho W^1_t + \sqrt{1-\rho^2} W^2_t \end{cases} \] où \(W = (W^1, W^2)\) est un mouvement Brownien bidimensionnel dont les composantes sont indépendantes.

def brownian_2d(n_paths: int,
                times: np.ndarray,
                correlation: float = 0., 
                increments: bool = False, 
                rng: np.random.Generator = None) -> np.ndarray:
    """
    Simule des trajectoires de mouvement brownien standard en 2D, avec 
    option de corrélation entre les 2 dimensions.

    Args:
        n_paths: Nombre de trajectoires à simuler.
        times: tableau 1d (list, tuple ou np.ndarray) de taille `n_times` 
               qui contient les instants $t_k$.
        correlation: Valeur du paramètre de corrélation $\rho \in [-1,1]$.
        increments: Si `True`, les accroissements sont retournés, 
                    sinon ce sont les trajectoires.
        rng: objet `Generator`, création si `None` (non recommandé).

    Returns:
        - si `increments=False`: np.ndarray de forme `(n_paths, n_times, 2)` 
          contenant les trajectoires aux instants $t_k$.
        - si `increments=True`: np.ndarray de forme `(n_paths, n_times-1, 2)`
          contenant les accroissements entre les instants $t_k$.
    """
    # Initialisation du générateur pseudo-aléatoire si non fourni
    if rng is None:
        rng = np.random.default_rng()

    # Calcul des accroissements avec corrélation 
    dt = np.diff(times)
    dW = np.sqrt(dt)[None,:,None] * rng.standard_normal((n_paths, len(dt), 2))

    dB = np.empty_like(dW)
    dB[:,:,0] = dW[:,:,0]
    dB[:,:,1] = correlation * dW[:,:,0] \
                + np.sqrt(1-correlation**2) * dW[:,:,1]

    # Si les accroissements sont demandés
    if increments:
        return dB

    # Construction des trajectoires browniennes (cumul des incréments)
    paths = np.hstack([np.zeros((n_paths,1,2)), np.cumsum(dB, axis=1)])
    return paths

N, M = 100, 200
T = 1
times = np.linspace(0, T, N)
## imes = np.arange(N+1)*(T / N)
rho = -0.7
paths = brownian_2d(M, times, correlation=rho)
## ns.lineplot(x=times, y=W2[0,:,0], color='C0', label='Dimension 1')
## ns.lineplot(x=times, y=W2[0,:,1], color='C1', label='Dimension 2')
fig, ax = plt.subplots()
for path in paths:
  ax.plot(path[:,0], path[:,1], color='C0', alpha=0.2)
ax.plot(paths[0,:,0], paths[0,:,1], color='C1', lw=2, label='One path')
ax.legend()
ax.set_title(fr"{M} 2d-Brownian motion paths with N={N}, $\rho = {rho}$");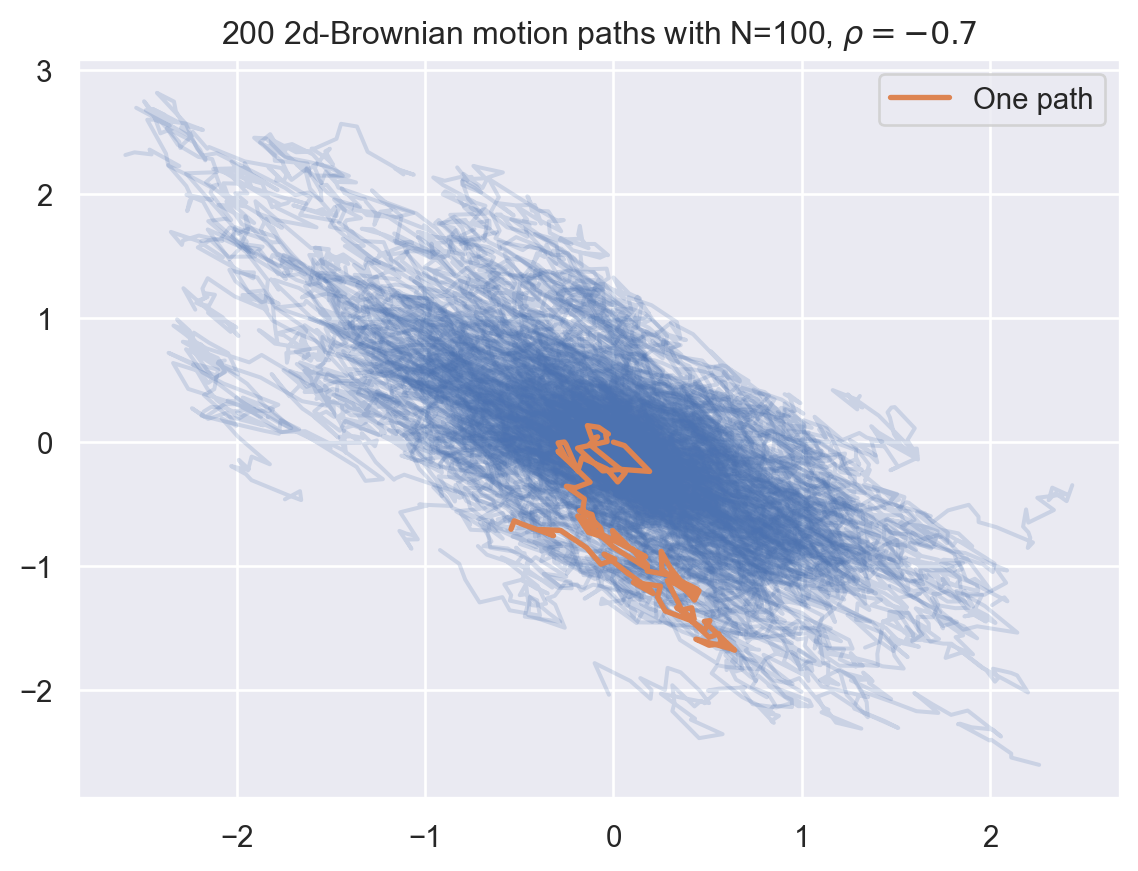

fig, ax = plt.subplots()
ax.plot(times, paths[0,:,0], color='C1', lw=2, ls='--', label='Dimension 1')
ax.plot(times, paths[0,:,1], color='C1', lw=2, ls=':', label='Dimension 2')
ax.legend()
ax.set_title(fr"A path as a function of time, $\rho = {rho}$");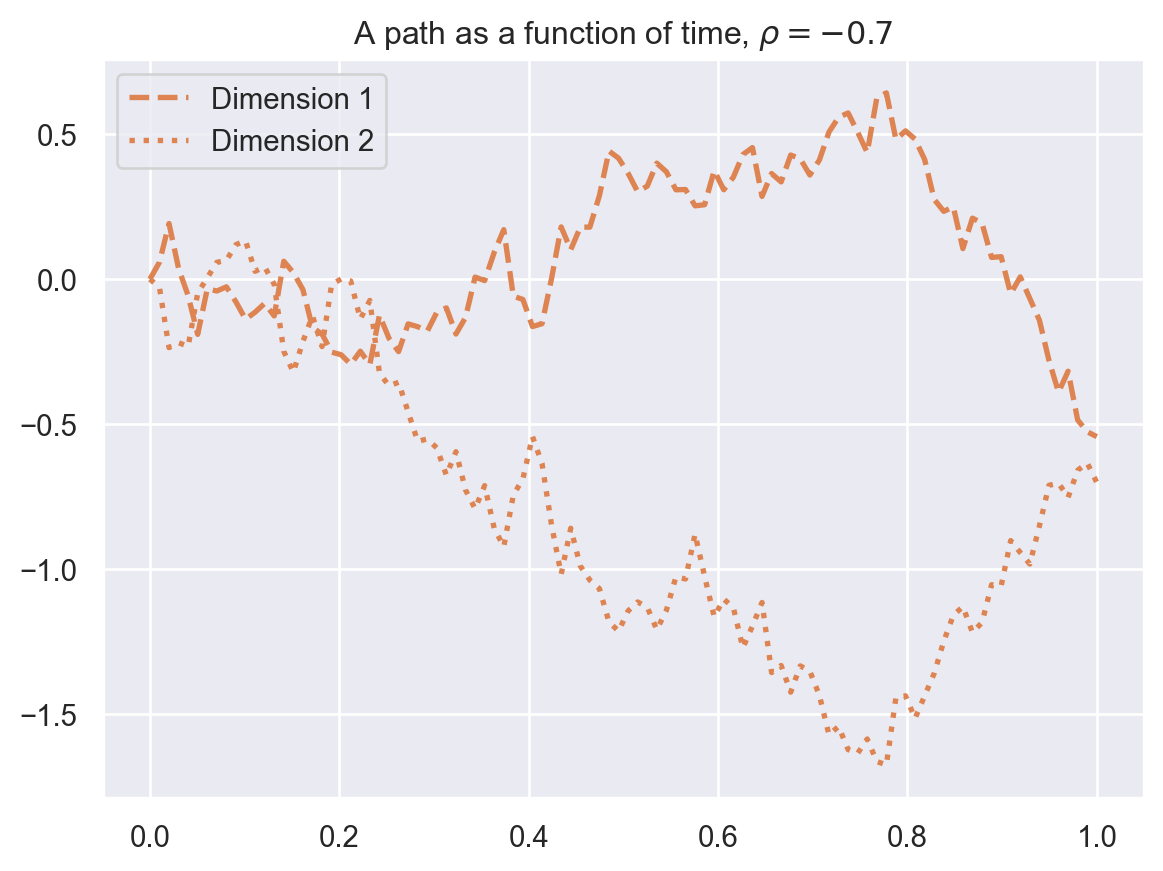

Important

Exercice: écrire un code pour vérifier que la corrélation empirique à chaque instant est bien “égale” à \(\rho = -0.7\). Vous pouvez faire 2 codes:

• en utilisant les opérations mean et std et en agissant sur les bons axes
• en utilisant la fonction np.corrcoef (lire la documentation): pour agir sur le temps il faut faire une boucle

W0, W1 = paths[:,1:,0], paths[:,1:,1]

## Solution à la main sans boucle 
cov_t = np.mean((W0 - W0.mean(axis=0)) * (W1 - W1.mean(axis=0)), axis=0)
corr_t = cov_t / (W0.std(axis=0) * W1.std(axis=0))

## Solution en utilisant np.corrcoef
corr_t = [np.corrcoef(W0[:, t], W1[:, t])[0, 1] for t in range(W0.shape[1])]

fig, ax = plt.subplots()
ax.plot(times[1:], corr_t, color='C2', lw=2, label='Empirical correlation')
ax.hlines(rho, times[1], times[-1], color='C3', label='True correlation')
ax.legend()
ax.set_title(fr"Empirical correlation as a function of time, $\rho = {rho}$");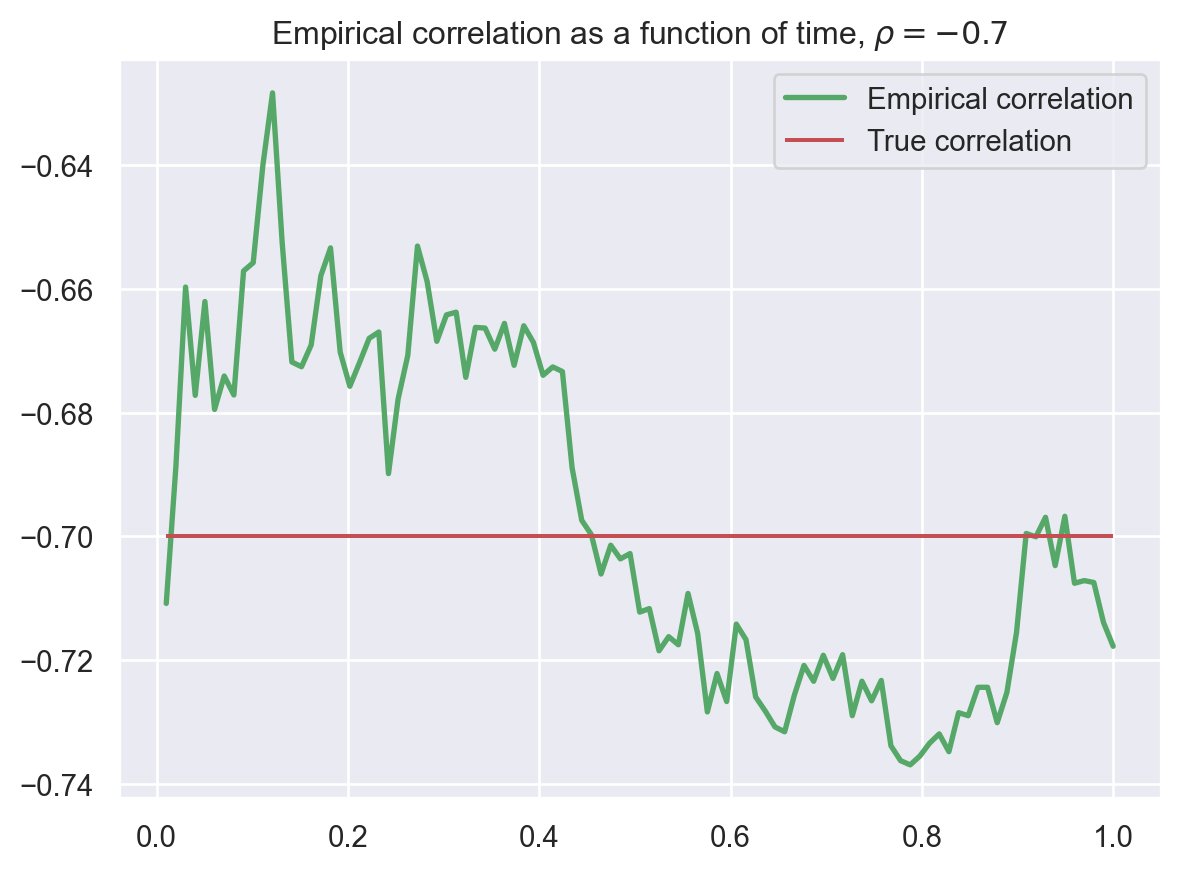

Note

Dans le tracé précédent il faudrait rajouter l’intervalle de confiance autour de chaque point de corrélation empirique!

1.2.2.2 Dimension \(d \ge 2\)

On suppose que la matrice de corrélation entre les dimensions est donnée par \(\Sigma\) une matrice symétrique définie positive.

Important

Exercice: écrire le code de la fonction brownian_md, vous pouvez faire la simulation à la main en utilisant la transormation de Cholesky de Sigma ou bien utiliser multivariate_normal (cf. doc).

1.3 Brownien Géométrique

Modèle classique pour représenter le cours d’un actif financier.

1.3.1 Dimension 1

On considère le processus \(S = (S_t)_{t \in [0,T]}\) solution de l’EDS sur \([0,T]\) \[ \operatorname{d}\!S_t = r S_t \operatorname{d}\!t + \sigma S_t \operatorname{d}\!B_t, \quad S_0 = x, \] c’est à dire (cf. cours calcul stochastique), pour tout \(t \in [0,T]\) \[ S_t = x \exp \bigl((r- \sigma^2/2) t + \sigma B_t \bigr). \]

def black_scholes_1d(n_paths: int,
                     times: np.ndarray,
                     init_value: float,
                     r: float, 
                     sigma: float,
                     rng: np.random.Generator = None) -> np.ndarray:
    """
    Simule des trajectoires de mouvement brownien standard en 1D.

    Args:
        n_paths: Nombre de trajectoires à simuler.
        times: tableau 1d (list, tuple ou np.ndarray) de taille `n_times` 
               qui contient les instants $t_k$.
        init_value: valeur initiale de l'actif 
        r: taux d'intérêt  
        sigma: volatilité de l'actif
        rng: objet `Generator`, création si `None` (non recommandé).

    Returns:
        - np.ndarray de forme `(n_paths, n_times)` contenant les 
        trajectoires aux instants $t_k$.
    """
    Bt = brownian_1d(n_paths, times, rng=rng)
    St = S0 * np.exp((r - 0.5*sigma**2) * times + sigma * Bt)

    return St

Voici un code illustrant l’utilisation de cette fonction.

T, N = 1, 100
times = np.arange(N+1)*(T / N)
S0, r, sigma = 100, 0.04, 0.20
M = 200
paths = black_scholes_1d(M, times, init_value=S0, r=r, sigma=sigma, rng=rng)

fig, ax = plt.subplots()
for path in paths:
    ax.plot(times, path, color='C0', alpha=0.3)
ax.plot(times, paths[0,:], color='C1', lw=2, label='One path')
ax.legend()
ax.set_title(f"{M} standard Black-Scholes paths with N={N} " \
             + fr"($r={r}$, $\sigma={sigma}$)");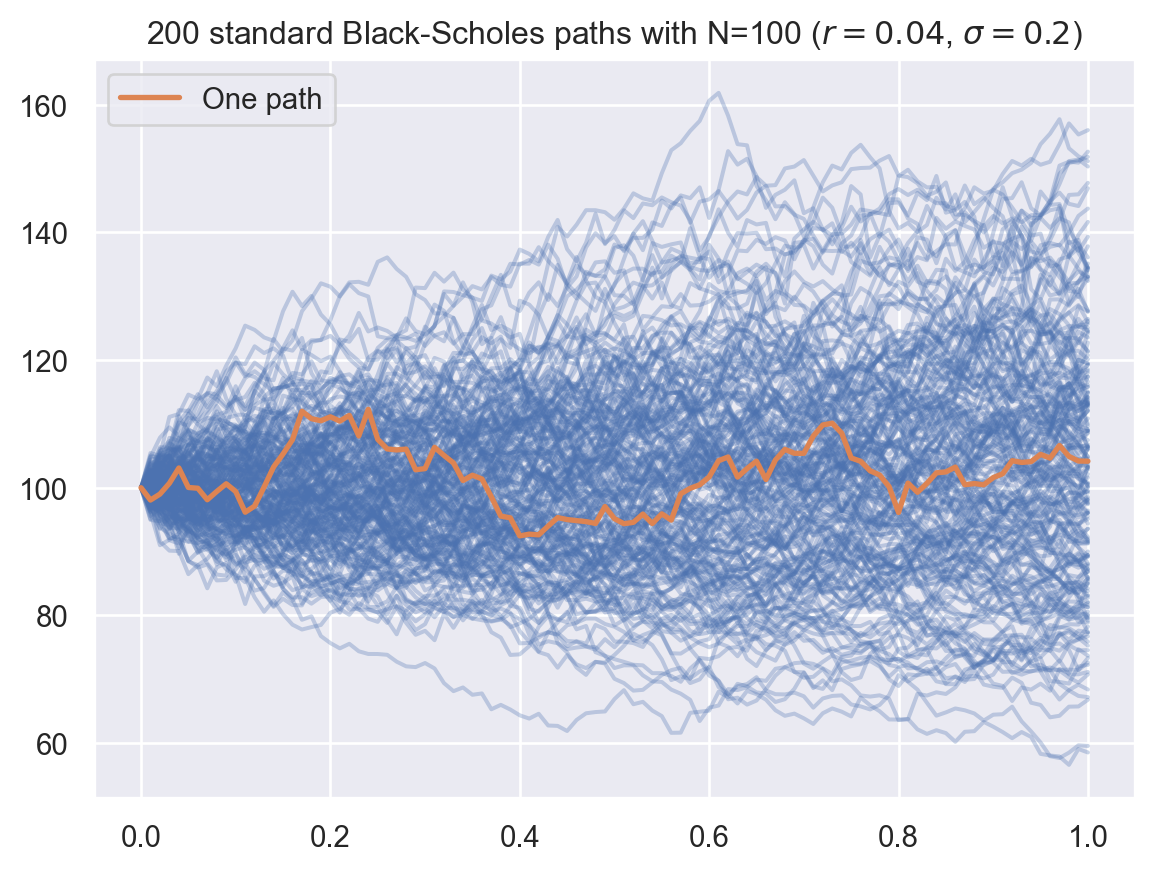

1.3.2 Dimension \(d \ge 2\)

(cf. projet Options Basket à la fin de la séance).

1.4 Méthode de Monte Carlo

Méthode numérique basée sur la loi des grands nombres et le théorème central limite pour donner un intervalle de confiance (asymptotique).

La seule valeur moyenne \(\bar I_M = \frac{1}{M} \sum_{k=1}^M X_k\) d’un échantillon \((X_1, \dots, X_M)\) n’est pas suffisante pour déterminer \(I = \mathbf{E}[X_1]\). Il faut toujours renvoyer la valeur de l’estimateur \(I_M\) et son intervalle de confiance \[ I \in \Bigl] \bar I_M- q_{1-\frac{\alpha}{2}} \frac{\sigma}{\sqrt{M}}; \bar I_M + q_{1 - \frac{\alpha}{2}} \frac{\sigma}{\sqrt{M}} \Bigr[ \quad \text{avec probabilité $p = 1-\alpha \in ]0,1[$} \] où \(q_{1-\frac{\alpha}{2}}\) est le quantile de niveau \(1-\frac{\alpha}{2}\) de la loi normale centrée réduite et \(\sigma^2 = \operatorname{var}(X_1)\).
Pour \(\alpha = 0.05\) c’est à dire \(p = 0.95\) on a \(1-\frac{\alpha}{2} = 1.96\).

Mise en garde

La moyenne seule ne suffit pas, il faut toujours donner l’intervalle de confiance.

def monte_carlo(sample: np.ndarray, proba: float = 0.95) -> dict:
    """
    Calcule l'estimation Monte Carlo de la moyenne d'un échantillon, et 
    fournit un intervalle de confiance pour la moyenne.

    Args:
    - sample (np.ndarray): Un tableau contenant les échantillons à analyser.
    - proba (float): Niveau de confiance pour l'intervalle (défaut: 0.95).

    Returns:
    - dict: Un dictionnaire contenant les valeurs suivantes :
        - "mean" (float): Moyenne de l'échantillon.
        - "var" (float): Variance de l'échantillon.
        - "lower" (float): Borne inférieure de l'intervalle de confiance.
        - "upper" (float): Borne supérieure de l'intervalle de confiance.
    """
    # Moyenne et variance de l'échantillon
    mean = np.mean(sample)
    var = np.var(sample, ddof=1)

    # Calcul de l'intervalle de confiance pour la moyenne
    alpha = 1 - proba
    quantile = sps.norm.ppf(1 - alpha / 2)
    ci_size = quantile * np.sqrt(var / sample.size)
    
    return {
        "mean": mean,
        "var": var,
        "lower": mean - ci_size,
        "upper": mean + ci_size
    }

Important

Exercice: Calculer le prix d’un Call dans un modèle de Black-Scholes par sa formule fermée et comparer le prix Monte Carlo pour différentes valeurs de \(M\).

S0, r, sigma = 100, 0.04, 0.2
K = 100
times = np.array([0, 1])

results = {} 
Ms = 10**np.arange(3, 8)
for M in Ms:
    St = black_scholes_1d(M, times, init_value=S0, r=r, sigma=sigma)
    payoffs = np.exp(-r*times[-1]) * np.maximum(St[:,-1] - K, 0)
    results[M] = monte_carlo(payoffs)

import pandas as pd
pd.DataFrame(results)

	1000	10000	100000	1000000	10000000
mean	10.189525	10.011290	10.018418	9.942382	9.921056
var	205.676795	208.728028	208.610724	208.745139	207.889365
lower	9.300650	9.728125	9.928899	9.914064	9.912119
upper	11.078400	10.294454	10.107938	9.970699	9.929992

def black_scholes_call(S0: float, K: float, T: float, 
                       r: float, sigma: float) -> float:
    """
    Calcule le prix d'un Call européen dans le modèle de Black-Scholes.

    Args:
    - S0 (float): Prix actuel de l'actif sous-jacent.
    - K (float): Prix d'exercice du Call.
    - T (float): Temps jusqu'à l'échéance en années.
    - r (float): Taux d'intérêt sans risque.
    - sigma (float): Volatilité du sous-jacent.

    Returns:
    - float: Prix du Call européen.
    """
    # Calcul des paramètres d1 et d2
    d1 = (np.log(S0 / K) + (r + 0.5 * sigma ** 2) * T) / (sigma * np.sqrt(T))
    d2 = d1 - sigma * np.sqrt(T)
    
    # Calcul du prix du Call
    call_price = S0 * sps.norm.cdf(d1) - K * np.exp(-r * T) * sps.norm.cdf(d2)
    return call_price

price = black_scholes_call(S0, K, T=1, r=r, sigma=sigma)
print("Prix par formule fermée:", price)

Prix par formule fermée: 9.925053717274437

1.4.1 Projet Options Basket: à préparer pour lundi 20 octobre

On considère \(d \ge 2\) actifs financiers dont la loi à l’instant \(T > 0\) est modélisée par une loi log-normale c’est à dire \[ \forall i \in \{1,\dots,d\}, \quad S^i_T = S^i_0 \exp\Bigl( \bigl(r-\frac{\sigma_i^2}{2}\bigr) T + \sigma_i \sqrt{T} \tilde G_i \Bigr) \] où le vecteur \((\tilde G_1,\dots, \tilde G_d)\) est gaussien centré de matrice de corrélation \(\Sigma\) et les constantes \(r > 0\), \(\sigma_i > 0\) sont fixées. Il s’agit d’actifs financiers \((S^i_t)_{t \in [0,T]}\), \(1 \le i \le d\), modélisés par un processus de Black-Scholes multidimensionnel. On introduit la matrice \(L\) triangulaire inférieure obtenue par la décomposition de Cholesky de la matrice \(\Sigma = L L^\top\).

A l’aide de cette matrice \(L\), on définit la fonction \(\Phi:\mathbf{R}^d \to \mathbf{R}^d\) telle que \[ (S^1_T, \dots, S^d_T) = \Phi(G_1, \dots, G_d) \quad \text{ou encore} \quad S^i_T = \Phi_i(G_1, \dots, G_d) \] où \((G_1, \dots, G_d) \sim \mathcal{N}(0, I_d)\) (l’égalité précédente est à considérer en loi).

On s’intéresse au prix d’une option européenne (aussi appelé produit dérivé européen) sur le panier de ces \(d\) actifs financiers, c’est à dire qu’on veut calculer \[ e^{-rT} \mathbf{E} \bigl[ X \bigr] \quad \text{avec} \quad X = \biggl(\frac{1}{d} \sum_{i=1}^d S^i_T - K\biggr)_+ \]

Note

• Implémenter un estimateur Monte Carlo pour calculer au centime près le prix pour différentes valeurs de \(K\), \(K \in \{80, 90, 100, 110, 120\}\).

• Implémenter les méthodes de réduction de variance suivantes, et comparer les temps de calcul et la complexité:

1. Méthode des variables antithétiques en considérant \((W^1_T, \dots, W^d_T)\) et \((-W^1_T, \dots, -W^d_T)\).
2. Utilisation de la variable de contrôle \[Y = \bigl(\bar S_0 e^Z - K\bigr)_+ \text{ avec } \bar S_0 = \frac{1}{d} \sum_{i=1}^d S^i_0\] et \(Z = \displaystyle \sum_{i=1}^d a^i_0 \big(\mu_i T + \sigma_i \sqrt{T} \tilde G_i\big)\) en posant \(a^i_0 = \displaystyle \frac{S^i_0}{\sum_{j=1}^d S^j_0}\) (t.q. \(\sum a^i_0 = 1\)).
3. Un mélange des 2 méthodes précédentes.