Motivation et simulations
A quoi ressemble un grand arbre choisi au hasard ? Et un graphe ? Peut-on justifier formellement l'impression que donne les simulations, à savoir que les `objets limites', si on peut les définir, sont fractals ?
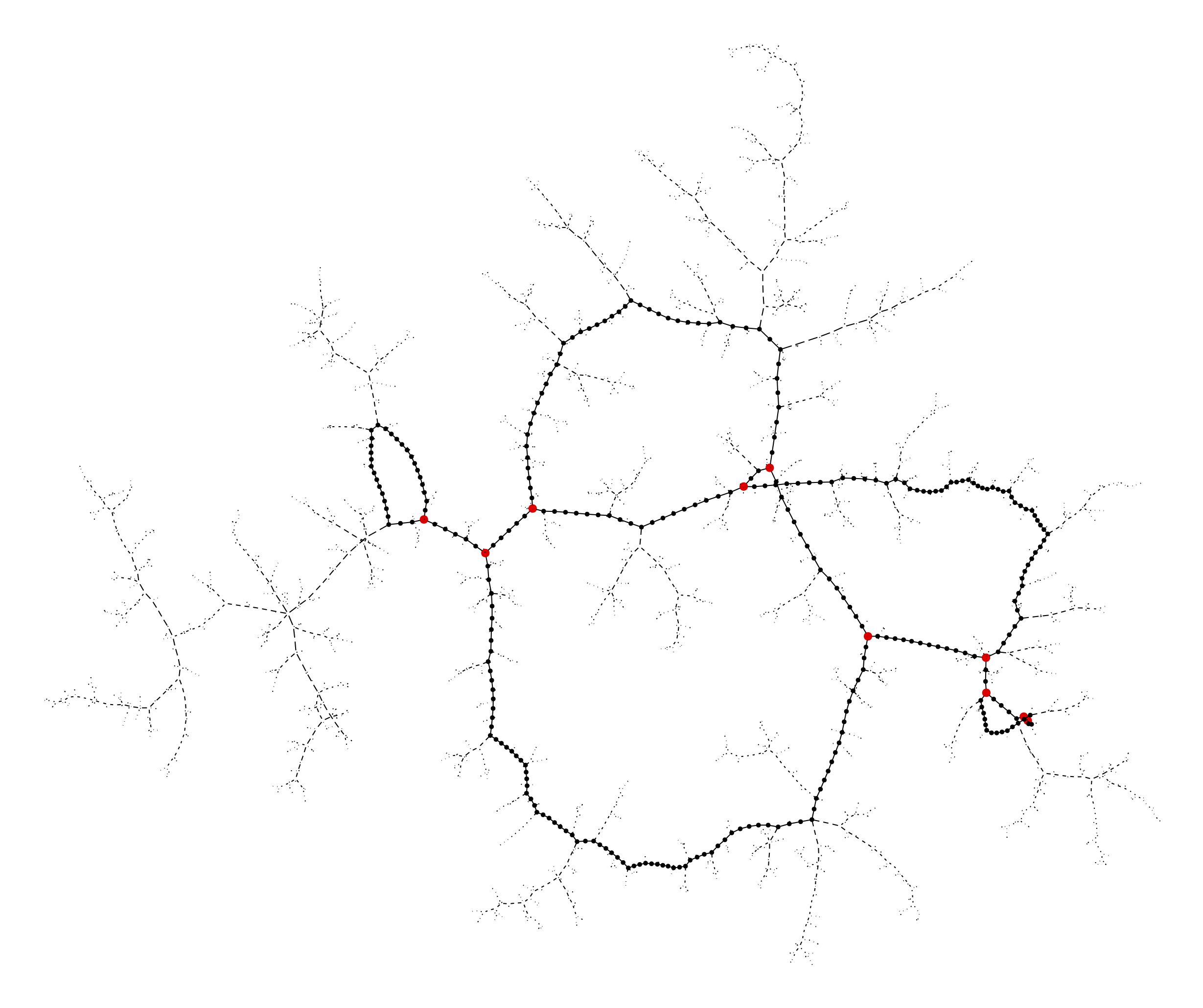
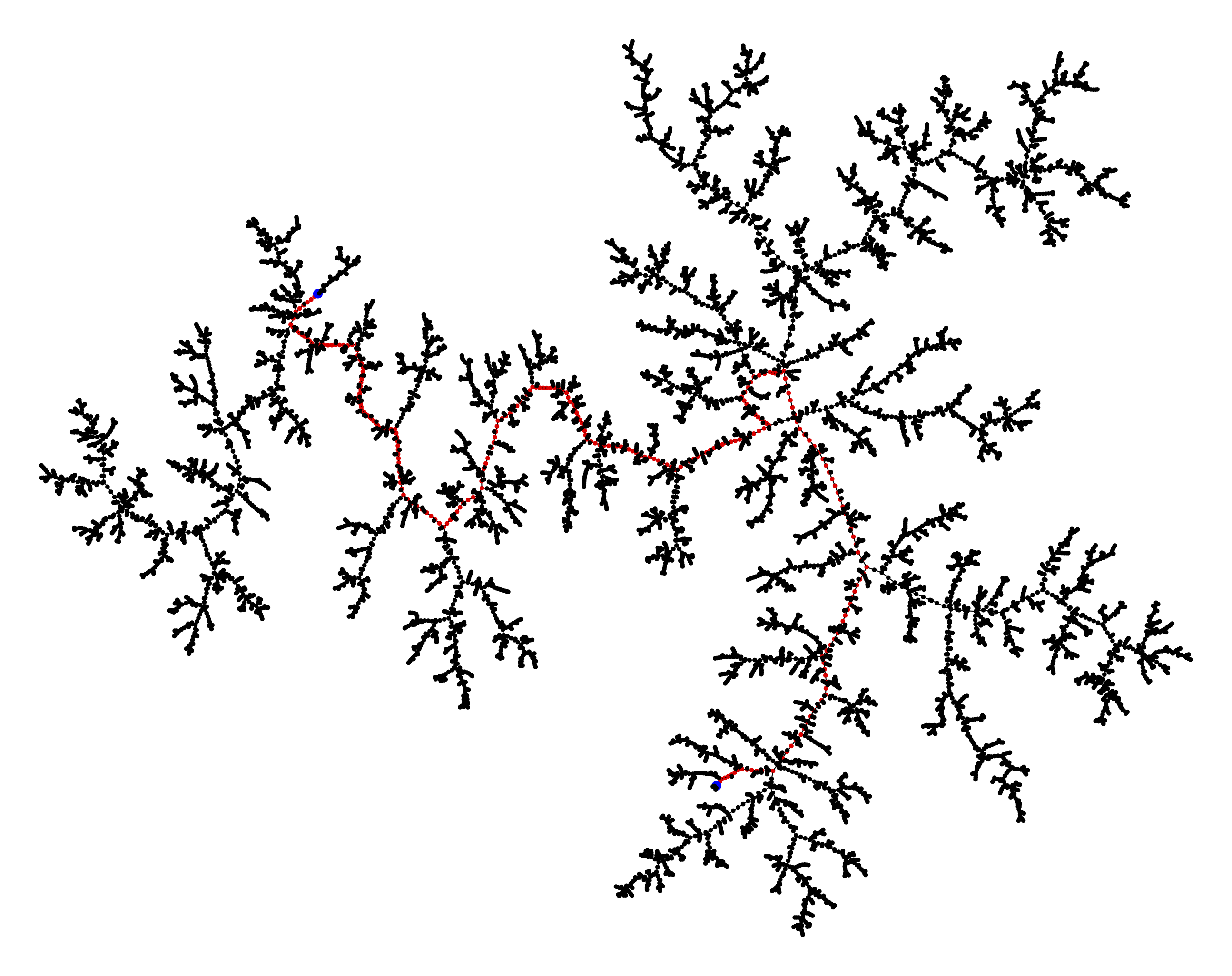
Séances: mercredis de 13:30 à 15:30 en 15-25.101 (Détails de l'emploi du temps ici). Cette année les séances sont par défaut de deux heures; certaines pourront durer 3h, notamment pour des TD, mais vous serez prévenus à l'avance
A quoi ressemble un grand arbre choisi au hasard ? Et un graphe ? Peut-on justifier formellement l'impression que donne les simulations, à savoir que les `objets limites', si on peut les définir, sont fractals ?
L'objet du cours est de tenter de répondre à ces questions et de présenter certaines limites de graphes aléatoires considérés en temps qu'espaces métriques. Il s'agira à la fois (a) d'introduire des objets centraux intimement liés au mouvement brownien, (b) de présenter un ensemble de techniques qui sont basées sur des représentations combinatoires explicites et (c) d'étudier les applications aux graphes aléatoires dans le régime dit critique. En particulier, les relations entre objets discrets et continus seront au centre de nos préoccupations.
Le cours comportera deux parties: dans un premier temps, nous considérerons des arbres aléatoires de type Galton--Watson et leurs limites. Nous parlerons en particulier des différents encodages des arbres, de leur convergences, ainsi que tu point de vue `objectif' qui consiste à les considérer comme des espaces métriques (mesurés); ca sera l'occasion de parler de la topologie de Gromov-Hausdorff sur les classes d'isométries d'espaces métriques compacts. Cela nous permettra d'introduire l'arbre continu brownien de plusieurs manières (en particulier comme métrique aléatoire sur $[0,1]$, ou encore par découpage de $\mathbb R_+$ et reorganisation/recollage des morceaux), et d'étudier certaines de ses propriétés. Nous verrons en particulier qu'il s'agit d'un objet fractal qui est au coeur de la construction de nombreux objets limites de structures combinatoires (de la même manière que le mouvement brownien est central pour les convergences fonctionnelles).
Nous verrons ensuite comment, à partir des techniques d'explorations, il est possible d'obtenir la limites de certains graphes aléatoires dans le régime dit `critique' qui précède l'émergence d'une composante connexe macroscopique. En particulier, nous construirons les objets limites à partir de l'arbre brownien continu. Là encore, nous nous efforcerons de développer plusieurs points de vue complémentaires. Nous parlerons aussi de processus de coalescence (en particulier le coalescent multiplicatif) que l'on peut définir comme le processus qui régit la dynamique des tailles des compososantes connexes d'un graphe aléatoire lorsque l'on ajoute des arêtes à la bonne vitesse.