3  Quasi-Monte Carlo

Exemple d’intégration de code C++

import math
import numpy as np
from numpy.random import default_rng
rng = default_rng()

from scipy import stats
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme()

3.1 Quasi-Monte Carlo

Le principe d’une méthode Quasi-Monte Carlo est de remplacer les nombres pseudo-aléatoires \((U_k)_{k \ge 1}\) par une suite déterministe \((\xi_k)_{k \ge 1}\) qui remplit mieux l’espace \([0,1]^d\). On mesure la qualité de répartition d’une suite dans \([0,1]^d\) par la notion de discrépance.

Supposons \(X\) une variable aléatoire à valeurs dans \(E \subset \mathbf{R}^d\). Supposons qu’il existe \(\Psi: [0,1]^q \to E\) telle que \(X \sim \Psi(U)\) où \(U \sim \mathcal{U}([0,1]^q)\). Par exemple si on note la fonction de répartition \(F_X(x) = \mathbf{P}[X \le x]\) et \(F_X^{-1}\) l’inverse généralisée de \(F_X\) (connue sous le nom de fonction quantile) alors \(X \sim F_X^{-1}(U)\) où \(U \sim \mathcal{U}([0,1])\) (ici \(q = 1\)).

Avec cette représentation de \(X\) on a \[ \mathbf{E}\big[\varphi(X)\big] = \mathbf{E}\big[ \varphi\big(\Psi(U)\big) \big] = \lim_{n \to +\infty} \frac{1}{n} \sum_{k=1}^n \varphi\big(\Psi(\xi_k)\big), \] où \((\xi_k)_{k \ge 1}\) est une suite à discrépance faible (Halton ou Sobol) sur \([0,1]^q\). Si \(\varphi \circ \Psi\) est à variation finie on a le résultat de Koksma-Hlawka pour contrôler l’erreur mais en pratique cette inégalité est difficilement appplicable car on ne connait pas la variation finie \(V(\varphi \circ \Psi)\).

Avertissement

La suite \((\xi_k)_{k \ge 1}\) n’est pas une suite de nombres pseudo-aléatoires car on ne demande pas la propriété d’indépendence de \(\xi_{k+1}\) par rapport à \(\xi_k\) (et plus généralement \(\sigma(\xi_j, j \le k)\)). Ne pas faire un code où l’on remplace naïvement les appels de \(U_k\) par \(\xi_k\).

Par exemple si vous simulez un coupe de Gaussiennes indépendantes par la méthode de Box-Muller à partir d’un couple \((U_{2k}, U_{2k+1})\) vous ne devez pas remplacer ce couple par \((\xi_{2k}, \xi_{2k+1})\). Il faut augmenter la dimension de la suite \((\xi_k)_{k \ge 1}\)

3.1.1 Koksma-Hlawka

Soit \((\xi_n)_{n \ge 1}\) une suite sur \([0,1]^d\) et \(f\) à variation \(V(f)\) finie. Alors \[\begin{equation*} \left|\frac{1}{n} \sum_{k=1}^n f(\xi_k) - \int_{[0,1]^d} f(u) d u \right| \le V(f) D_n^*(\xi), \end{equation*}\] où \(D_n^*(\xi)\) est la discrépance de la suite \((\xi_n)_{n \ge 1}\) définie par \[\begin{equation*} D_n^*(\xi) = \sup_{x \in [0,1]^d} \left|\frac{1}{n} \sum_{k=1}^n \mathbf{1}_{[0,x]}(\xi_k) - \prod_{i=1}^d x^i\right| \end{equation*}\]

Une méthode de Quasi-Monte Carlo est similaire à une méthode de Monte Carlo où les nombres pseudo-aléatoires sont remplacés par des suites dites à discrépance faible, c’est à dire dont la discrépance vérifie: \[\begin{equation*} D_n^*(\xi) = \mathcal{O}\left( \frac{(\log n)^d}{n} \right) \end{equation*}\]

Important

Si \((U_n)_{n \ge 1}\) est une suite i.i.d. uniformément distribuée sur \([0,1]^d\), alors (par la loi du logarithme itéré) \[\begin{equation*} \limsup_n \sqrt{\frac{2n}{\log(\log n)}} D_n^*(U) = 1 \quad p.s. \end{equation*}\] La discrépance est donc de l’ordre de \(\sqrt{\log(\log(n))} / \sqrt{2n}\).

Note

La borne déterminisite donnée par le résultat de Koksma-Hlawka permet de donner un intervalle de confiance mais il faut connaitre la variation \(V(f)\) de la fonction et même en connaissant cette quantité l’intervalle est beaucoup trop grand par rapport aux observations empiriques. D’autre part une méthode fonctionne même lorsque la fonction est à variation infinie \(V(f) = +\infty\).

Dans le cas d’une méthode “randomisée” Random Quasi-Monte Carlo on peut répliquer \(K\) fois l’estimateur (\(K\) petit, par exemple 10) et déduire un intervalle de confiance empirique (cf. section 3 sur les options basket).

3.2 Suites à discrépance faible

3.2.1 Suite de Van der Corput \((d = 1)\)

La suite de Van der Corput repose sur la manipulation des coefficients de la décomposition \(p-\)adique de \(n \ge 1\):

• Soit \(p\) un nombre premier qui sert de base à la décomposition \(p-\)adique
• Décomposition de \(n\): \[\begin{equation*} n = a_0 + a_1 p + \dots a_r p^r, \quad a_k \in \{0, \dots, p-1\}, \quad a_r \neq 0, \end{equation*}\]
• Construction de \(\xi^{(p)}_n\) appelée dans la suite VdC en base \(p\):
  \[\begin{equation*} \xi^{(p)}_n = \frac{a_0}{p} + \frac{a_1}{p^2} + \dots + \frac{a_r}{p^{r+1}} \in [0,1]. \end{equation*}\]

Discrépance: \[\begin{equation*} D_n^*(\xi^{(p)}) \le \frac{1}{n} \left(1 + (p-1) \frac{\log(p n)}{\log(p)}\right) \end{equation*}\]

Important

Montrer que \[ \lim_{n \to \infty} \frac{1}{n} \sum_{k=1}^n \xi^{(2)}_{2k} \xi^{(2)}_{2k+1} = \frac{5}{24} \] alors que si \((U_n)_{n \ge 1}\) suite i.i.d. uniforme sur \((0,1)\) \[ \lim_{n \to \infty} \frac{1}{n} \sum_{k=1}^n U_{2k} U_{2k+1} = \frac{1}{4}. \]

3.2.1.1 Implémentation naïve

L’idée la plus simple consiste à décomposer \(n\) en base \(p\) pour obtenir les coefficients \(a_0, \dots, a_r\) puis de construire \(\xi_n^{(p)}\).

Note

Voici un code que l’on peut obtenir sur le site rosettacode.org. Ce site est utile et instructif pour trouver des algorithmes correctement écrits dans plusieurs langages de programmation.

def vdc(n, p=2):
    xi_n, denom = 0, 1
    while n:
        denom *= p
        n, remainder = divmod(n, p)
        xi_n += remainder / denom
    return xi_n

Si on veut construire les \(n = 100\,000\) premières itérations, on itère les appels de la fonction vdc. Cela ne semble pas optimal et en effet le temps d’exécution moyen est très lent.

n = int(1e6)
print(f"Temps d'exécution pour {n} itérations:")
%timeit np.array([vdc(i, p=2) for i in range(n)])
%timeit np.array([vdc(i, p=11) for i in range(n)])
print(f"Pour comparaison, un échantillon de {n} nombres pseudo-aléatoires:")
%timeit rng.random(n)

Temps d'exécution pour 1000000 itérations:
1.03 s ± 7.39 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
340 ms ± 1.89 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
Pour comparaison, un échantillon de 1000000 nombres pseudo-aléatoires:
2.93 ms ± 4.13 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)

3.2.1.2 Représentation des premiers points pour différentes bases

On affiche les premières itérations de la suite de VdC pour les premières bases \(p=2, 3, 5, 7\). La construction montre une certaine régularité, visible lorsque \(p\) augmente.

n = 150
fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(8, 6), 
                        sharex=True, sharey=True, layout='tight')
for ax, p in zip(axs.flat, [2, 3, 5, 7]): 
    xi_n = [ vdc(k, p=p) for k in range(n) ]
    ax.scatter(np.arange(n), xi_n, s=10, marker='X', alpha=0.5)
    ax.set_title(f"base p = {p}")
fig.suptitle(f"The first {n} iterations of the VdC sequence.")
plt.show()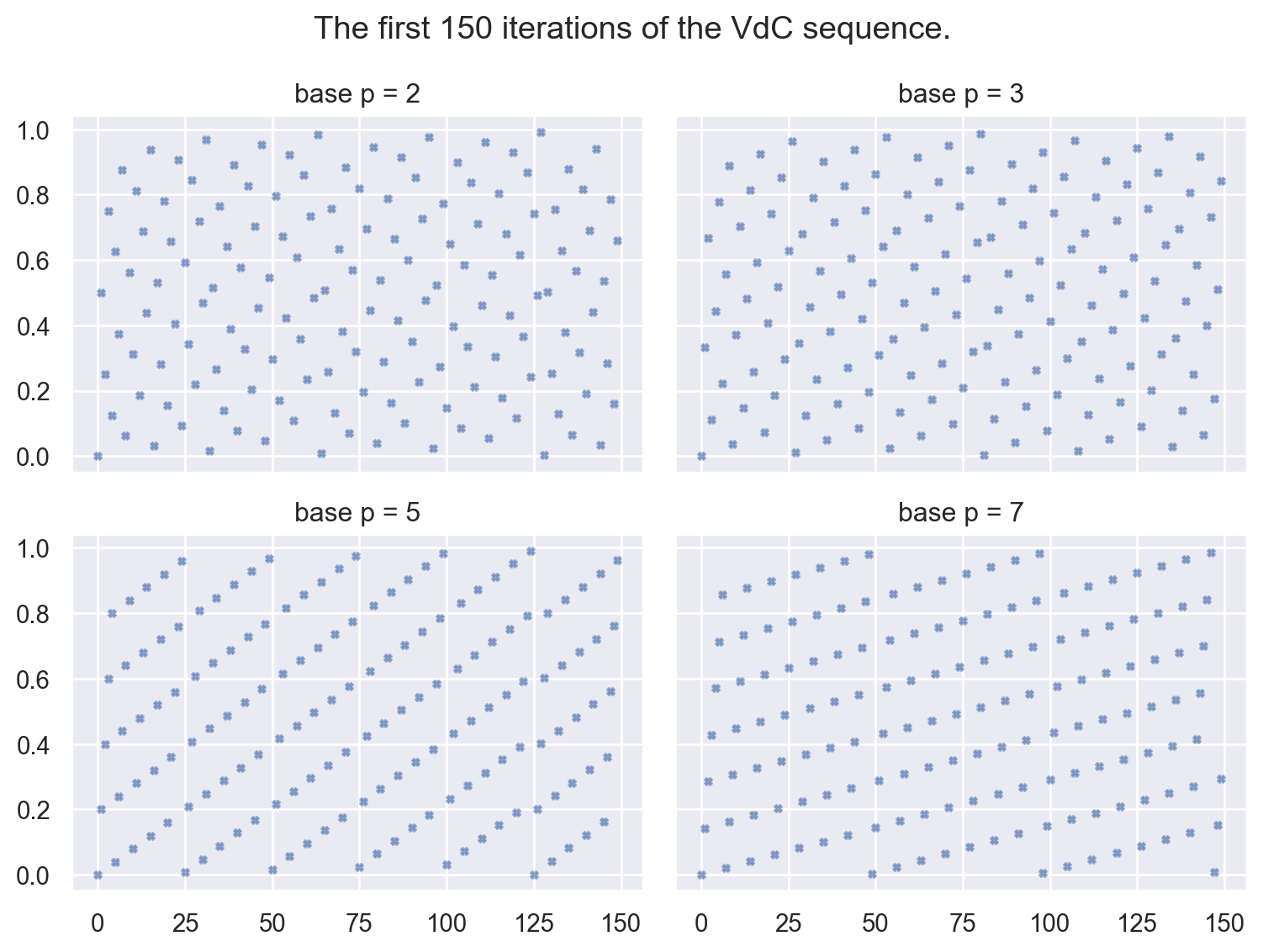

3.2.1.3 Implémentation améliorée en numpy

L’idée est de construire directement une plage d’itérations de la suite \((\xi^{(p)}_n)_{n \ge 0}\). On note \([r]_p\) le vecteur des \(p^r\) premières itérations et \(\xi^{(p)}_{[r]_p}\) les éléments de la suite de Van der Corput associée \[ [r]_p = \big(0, 1, \dots, p^r-1) \quad \text{et} \quad \xi^{(p)}_{[r]_p} = \big( \xi^{(p)}_0, \xi^{(p)}_1, \dots, \xi^{(p)}_{p^r-1} \big) \]

Note

La construction du vecteur à \(p^{r+1}\) éléments \([r+1]_{p}\) se fait à partir du vecteur \([r]_p\) en posant: \[ [r+1]_{p} = \big( [r]_p \;,\; [r]_p + p^r \;,\; [r]_p + 2p^r \;,\; \dots \;,\; [r]_p + (p-1) p^r \big) \] (la concaténation de \(p\) vecteurs de taille \(p^r\)).

En numpy on peut utiliser le broadcasting pour construire efficacement \([r+1]_{p}\) à partir de \([r]_{p}\). On a \([1]_{p}\) qui correspond à np.arange(p) et voici comment construire \([2]_p\) puis \([3]_p\)

p = 3
coeffs = np.arange(p).reshape(-1, 1)
u1 = coeffs.flatten()
print(u1)
u2 = (u1 + coeffs * p).flatten()
print(u2)
u3 = (u2 + coeffs * p**2).flatten()
print(u3)

[0 1 2]
[0 1 2 3 4 5 6 7 8]
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
 24 25 26]

De la même façon on peut construire les \(p^{r+1}\) premières itérations de la suite de VdC à partir d’une transformation simple des \(p^r\) premières itérations. Plus préciseement on a \[ \xi^{(p)}_{[r+1]_p} = \Big( \xi^{(p)}_{[r]_p} \;,\; \xi^{(p)}_{[r]_p} + \frac{1}{p^{r+1}} \;,\; \dots \;,\; \xi^{(p)}_{[r]_p} + \frac{p-1}{p^{r+1}} \Big) \]

def van_der_corput_r(r: int, p: int):
    """ Produce the Van der Corput sequence from 0 to p**r-1. """
    coeffs = np.arange(p).reshape(-1, 1)
    seq = (coeffs / p).reshape(-1)
    for k in range(2, r+1):
        seq = (seq + coeffs / p**k).reshape(-1)
    return seq

van_der_corput_r(r=3, p=2) 

array([0.   , 0.5  , 0.25 , 0.75 , 0.125, 0.625, 0.375, 0.875])

On écrit alors une fonction van_der_corput qui génère la suite jusqu’à l’itération \(n\) donnée. Il suffit de déterminer \(r\) tel que \(p^{r-1}\le n < p^{r}\).

def van_der_corput(n: int, p: int):
    """ Produce the Van der Corput sequence from 0 to n. """
    r = math.ceil(math.log(n) / math.log(p))
    seq = van_der_corput_r(r, p)
    return seq[:n]

Avec cette implémentation purement numpy et non python on obtient des temps du même ordre de grandeur que les nombres pseudos-aléatoires (générés en interne en C++).

n = int(1e6)
%timeit van_der_corput(n, p=2)
%timeit van_der_corput(n, p=11)

293 μs ± 728 ns per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
257 μs ± 236 ns per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

3.2.2 Suite de Halton

Soit \(d\) la dimension, et \(p_1,\dots, p_d\) les \(d\) premiers nombres premiers.

La suite de Halton en dimension \(d \ge 2\) est définie à partir des suites de Van der Corput dans les différentes bases \(p_1, \dots, p_d\) \[\begin{equation*} \Xi^{(d)}_n = (\xi^{(p_1)}_n, \dots, \xi^{(p_d)}_n) \end{equation*}\]

Discrépance: \[\begin{equation*} D_n^*(\Xi^{(d)}) \le \frac{1}{n} \left(1 + \prod_{i=1}^d(p_i-1) \frac{\log(p_i n)}{\log(p_i)}\right) \end{equation*}\]

def halton(n: int = 10, d: int = 2):
    """ Halton sequence in dimension d from 0 to n. """
    """ Warning: only for d < 25"""
    primes = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 
              43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
    result = [ van_der_corput(n, primes[k]) for k in range(d) ]
    return np.array(result).T

halton(n=7, d=5)

array([[0.        , 0.        , 0.        , 0.        , 0.        ],
       [0.5       , 0.33333333, 0.2       , 0.14285714, 0.09090909],
       [0.25      , 0.66666667, 0.4       , 0.28571429, 0.18181818],
       [0.75      , 0.11111111, 0.6       , 0.42857143, 0.27272727],
       [0.125     , 0.44444444, 0.8       , 0.57142857, 0.36363636],
       [0.625     , 0.77777778, 0.04      , 0.71428571, 0.45454545],
       [0.375     , 0.22222222, 0.24      , 0.85714286, 0.54545455]])

3.2.2.1 Représentation graphique

Attention pour la suite de Halton ainsi construite on a un effet indésirable qui apparaît lorsque la dimension augmente.

sample = halton(n = 1000, d=20)     # faire avec n = 5000...

fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(8, 4.5), layout='tight')
ax1.scatter(sample[:,0], sample[:,1], s=10, marker='o', alpha=0.5)
ax1.set_title("The first two dimensions: p=2, p=3")
ax2.scatter(sample[:,-2], sample[:,-1], s=10, marker='o', alpha=0.5) 
ax2.set_title("The last two dimensions: p=67, p=71")
fig.suptitle("The first 1000 points of the Halton sequence in dimension 20")
plt.show()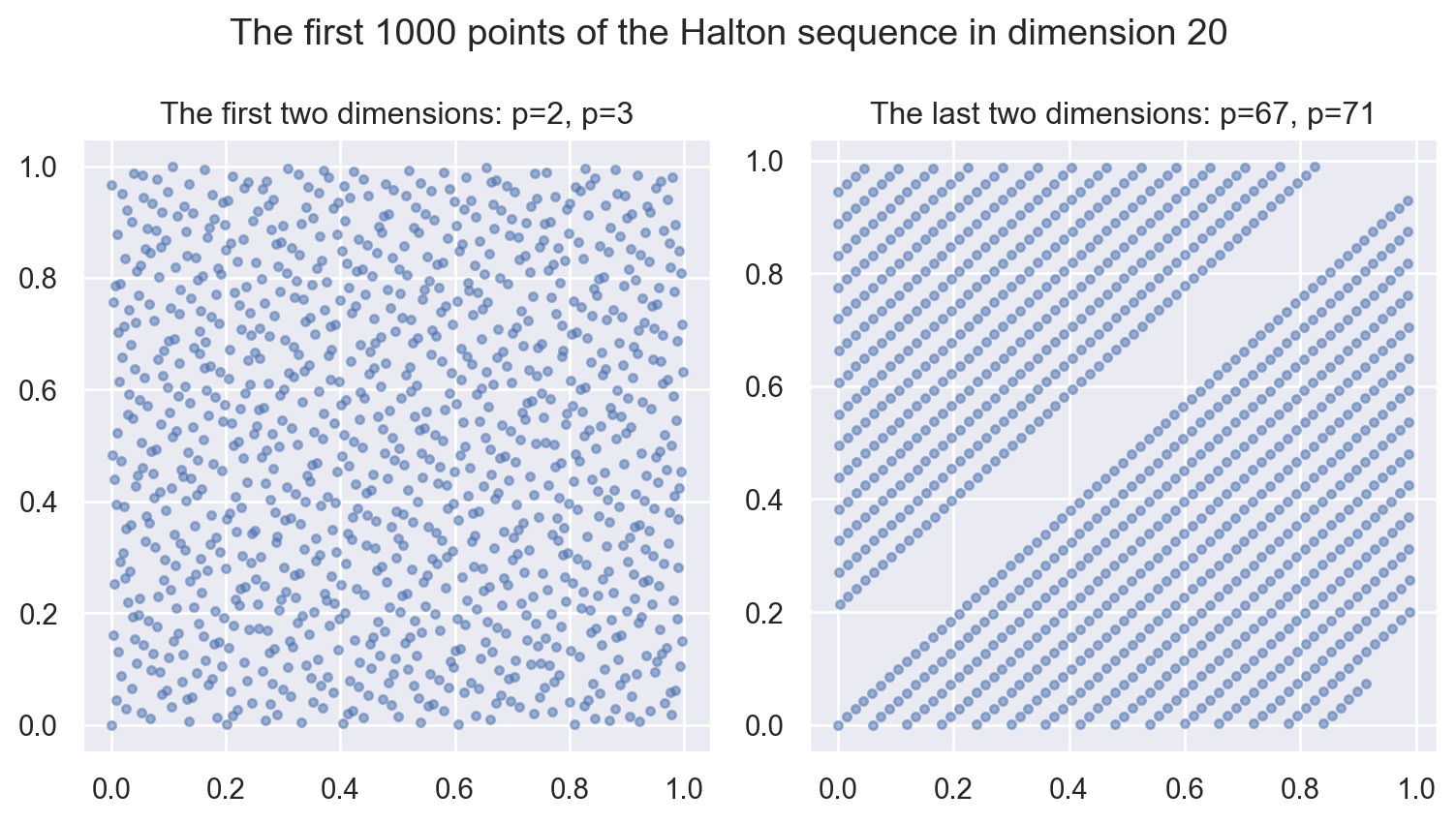

3.2.2.2 Utilisation de scipy

Dans le sous-module qmc du module stats de scipy vous trouvez de nombreux algorithmes pour le Quasi-Monte Carlo. En particulier il y a une classe Halton pour générer une suite de Halton. Le constructeur demande la dimension du problème d. Lorsque l’objet est créé, la méthode random prend un argument n et renvoie les n prochaines valeurs de la suite de Halton.

Pour plus d’information il faut consulter la page d’aide: ?stats.qmc.Halton.

halt = stats.qmc.Halton(d=5, scramble=False) 
## on discute de l'option `scramble` dans la section suivante
halt.random(n = 7)

array([[0.        , 0.        , 0.        , 0.        , 0.        ],
       [0.5       , 0.33333333, 0.2       , 0.14285714, 0.09090909],
       [0.25      , 0.66666667, 0.4       , 0.28571429, 0.18181818],
       [0.75      , 0.11111111, 0.6       , 0.42857143, 0.27272727],
       [0.125     , 0.44444444, 0.8       , 0.57142857, 0.36363636],
       [0.625     , 0.77777778, 0.04      , 0.71428571, 0.45454545],
       [0.375     , 0.22222222, 0.24      , 0.85714286, 0.54545455]])

Avertissement

Le nom de la méthode random est très mal choisi: ce n’est pas aléatoire, mais on comprend que cet appel renvoie les n=7 premières itérations de la suite, avec modification de l’état interne. Si on appel de nouveau la méthode random sur l’objet halt on obtient les itérations suivantes.

Note

On peut vérifier que les 2 algorithmes déterministes (le notre et celui de scipy) construisent la même suite par exemple en calculant l’erreur \(\ell^1\) totale (qui ne contient que la somme des erreurs d’arrondies):

halt = stats.qmc.Halton(d=5, scramble=False)
n = int(1e6)
np.sum(np.abs(halt.random(n) - halton(n, d=5)))

np.float64(5.3544276098166554e-11)

3.2.2.3 Perturbation

Pour atténuer l’effet de ligne en grande dimension qui est du à la trop grande régularité dans la construction des suites de Van der Corput on peut “agiter” un peu cette construction. Plus précisément on perturbe la construction en considérant une permutation des coefficients apparaissant dans la décomposition p-adique.

L’algorithme de perturbation implémenté via l’option scramble est issu de l’article A randomized Halton algorithm in R.

halt = stats.qmc.Halton(d=20, scramble=True)
sample = halt.random(n=1000)

fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(8, 4), layout='tight')
ax1.scatter(sample[:,0], sample[:,1], s=10, marker='o', alpha=0.5)
ax1.set_title("The first two dimensions: p=2, p=3")
ax2.scatter(sample[:,-2], sample[:,-1], s=10, marker='o', alpha=0.5) 
ax2.set_title("The last two dimensions: p=67, p=71")
plt.show()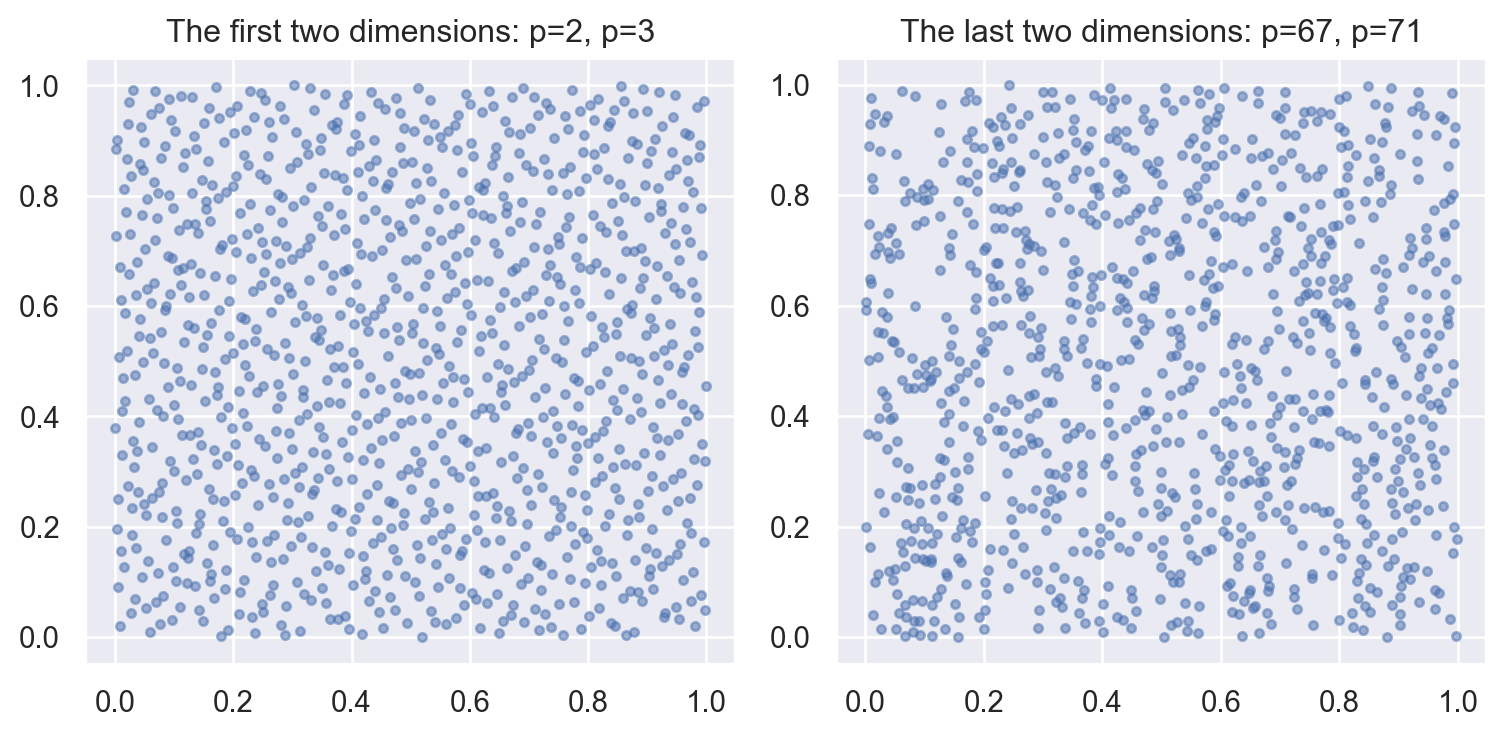

3.2.2.3.1 Retour sur Van der Corput et on l’agite!

On revient sur le code précédent et on applique cette idée de permutation des coefficients. Dans notre approche, cela se fait en utilisant la fonction rng.shuffle qui applique une permutation aléatoire aux coefficients coeffs.

def van_der_corput_r(r: int, p: int, scramble: bool=True):
    """ Produce the Van der Corput sequence from 0 to p**r-1 (with scramble option). """
    coeffs = np.arange(p)[np.newaxis]
    if scramble: 
        rng.shuffle(coeffs, axis=1)
    seq = coeffs / p
    for k in range(2, r+1):
        if scramble: 
            rng.shuffle(coeffs, axis=1)
        seq = (seq + coeffs.T/p**k).reshape((1, -1))
    seq = seq.flatten()
    return seq

def van_der_corput(n: int, p: int, scramble: bool=True):
    """ Produce the Van der Corput sequence from 0 to n (with scramble option). """
    r = math.ceil(math.log(n) / math.log(p))
    seq = van_der_corput_r(r, p, scramble)
    return seq[:n]

n = 150
fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(8, 6), 
                        sharex=True, sharey=True, layout='tight')
for ax, p in zip(axs.flat, [2, 3, 5, 7]): 
    xi_n = van_der_corput(n, p)
    ax.scatter(np.arange(n), xi_n, s=10, marker='X', alpha=0.5)
    ax.set_title(f"base p = {p}")
fig.suptitle(f"The first {n} iterations of the randomly permuted VdC sequence.")
plt.show()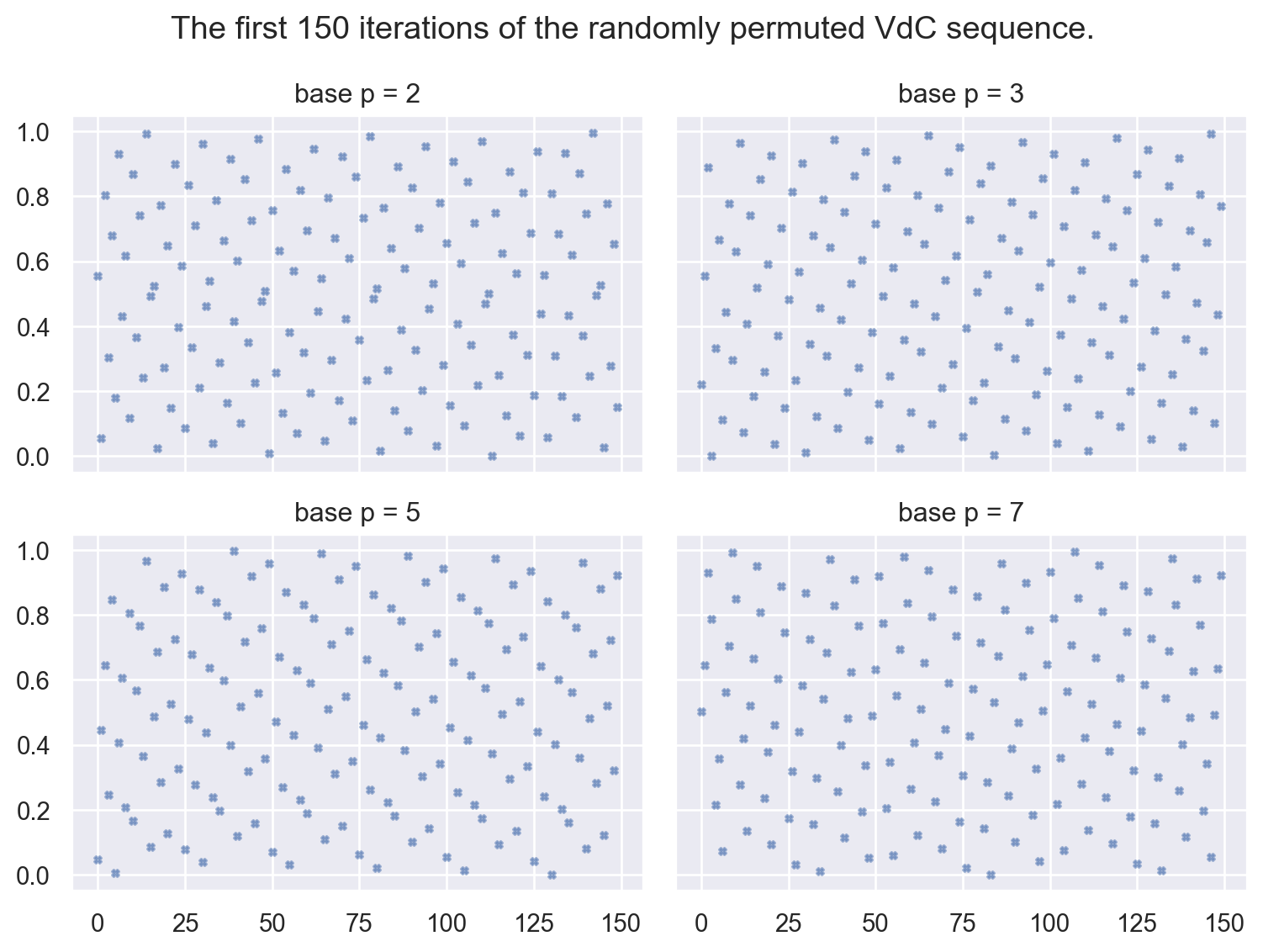

sample = halton(n = 1000, d=20)     # faire avec n = 5000...

fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(8, 4.5), layout='tight')
ax1.scatter(sample[:,0], sample[:,1], s=10, marker='o', alpha=0.5)
ax1.set_title("The first two dimensions: p=2, p=3")
ax2.scatter(sample[:,-2], sample[:,-1], s=10, marker='o', alpha=0.5) 
ax2.set_title("The last two dimensions: p=67, p=71")
fig.suptitle("The first 1000 points of the scrambled Halton sequence in dimension 20")
plt.show()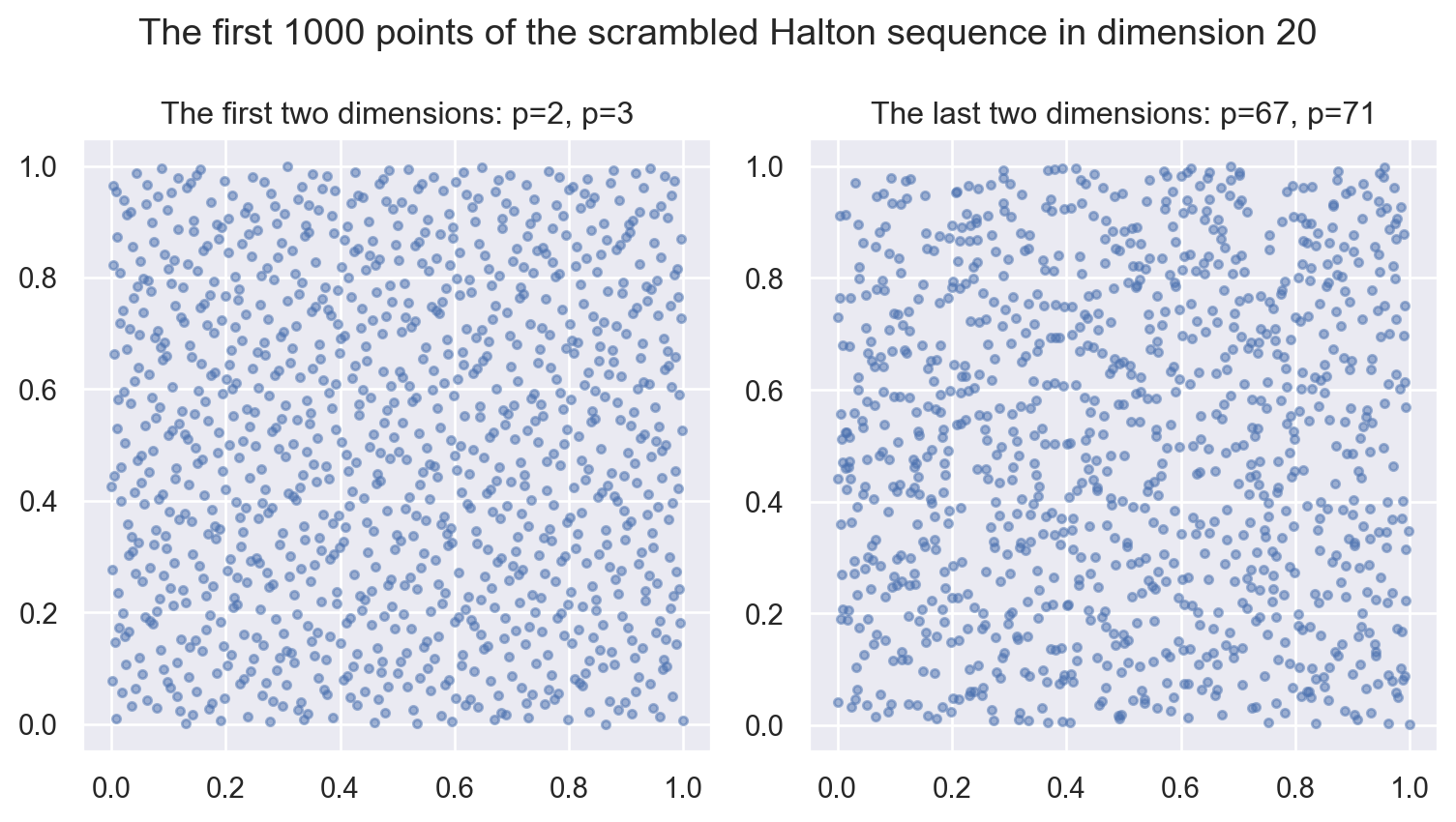

3.2.2.4 Allons voir le code utilisé dans scipy: cython inside

Si on cherche dans les sources de scipy on trouve à la ligne 373 du fichier sur github la définition de la fonction _cy_van_der_corput_threaded_loop. En fait ce n’est pas une fonction écrite en python mais en cython. Le langage cython permet d’écrire des fonctions C qui seront compilés et utilisables facilement en python. C’est une des approches pour interfacer le C et le python.

Vous pouvez voir plus de détails sur la page de tutoriel.

Note

On peut comparer les temps de simulation entre le code cython de scipy et notre code maison en numpy. Notre implémentation est plus efficace.

n = int(1e6)
halt = stats.qmc.Halton(d=5)
%timeit -o halton(d=5, n=n)    # version optimisée en numpy
%timeit -o halt.random(n=n)    # version scipy (cython)

4.9 ms ± 8.67 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)
121 ms ± 154 μs per loop (mean ± std. dev. of 7 runs, 10 loops each)

<TimeitResult : 121 ms ± 154 μs per loop (mean ± std. dev. of 7 runs, 10 loops each)>

A retenir: Un compilateur peut vous faire gagner un facteur 10 ou 100, mais c’est aussi le cas pour un changement d’algorithme!

3.2.3 Suite de Sobol

L’algorithme le plus populaire pour les suites à discrépances faible. La génération d’une suite de Sobol est très rapide car toute l’arithmétique se fait en base 2 (à la différence de la suite de Halton). De plus la représentation binaire d’un entier n peut se faire en utilisant le code de Gray qui permet d’avoir la modification d’un seul bit entre 2 entiers consécutifs.

L’algorithme de Sobol dépend de paramètres à définir (un peu comme les paramètres d’un générateur de nombres pseudo-aléatoires). Il est très important de bien initialiser ces paramètres (les directions).

On recommande d’utiliser uniquement des algorithmes déjà codés, testés et éprouvés! Il ne faut pas recoder son prore algorithme qui sera peut-être invalide.

3.2.3.1 Utilisation de scipy

La classe Sobol du module stats.qmc s’utilise de la même façon que la classe Halton. On peut voir que l’algorithme est très rapide. Le warning indique qu’il vaut mieux travailler avec \(n\) qui est une puissance de 2.

from scipy import stats
Sob = stats.qmc.Sobol(5, scramble=False)
nbig = int(1e6)
#%timeit Sob.random(nbig)

n, d = 2**10, 20
sob = stats.qmc.Sobol(d=d, scramble=False)
sample = sob.random(n=n)

fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(8, 4.5), layout='tight')
ax1.scatter(sample[:,0], sample[:,1], s=10, marker='o', alpha=0.5)
ax1.set_title("The first two dimensions")
ax2.scatter(sample[:,-2], sample[:,-1], s=10, marker='o', alpha=0.5) 
ax2.set_title("The last two dimensions")
fig.suptitle(f"The first {n} iterations of the Sobol sequence in dimension {d}.")
plt.show()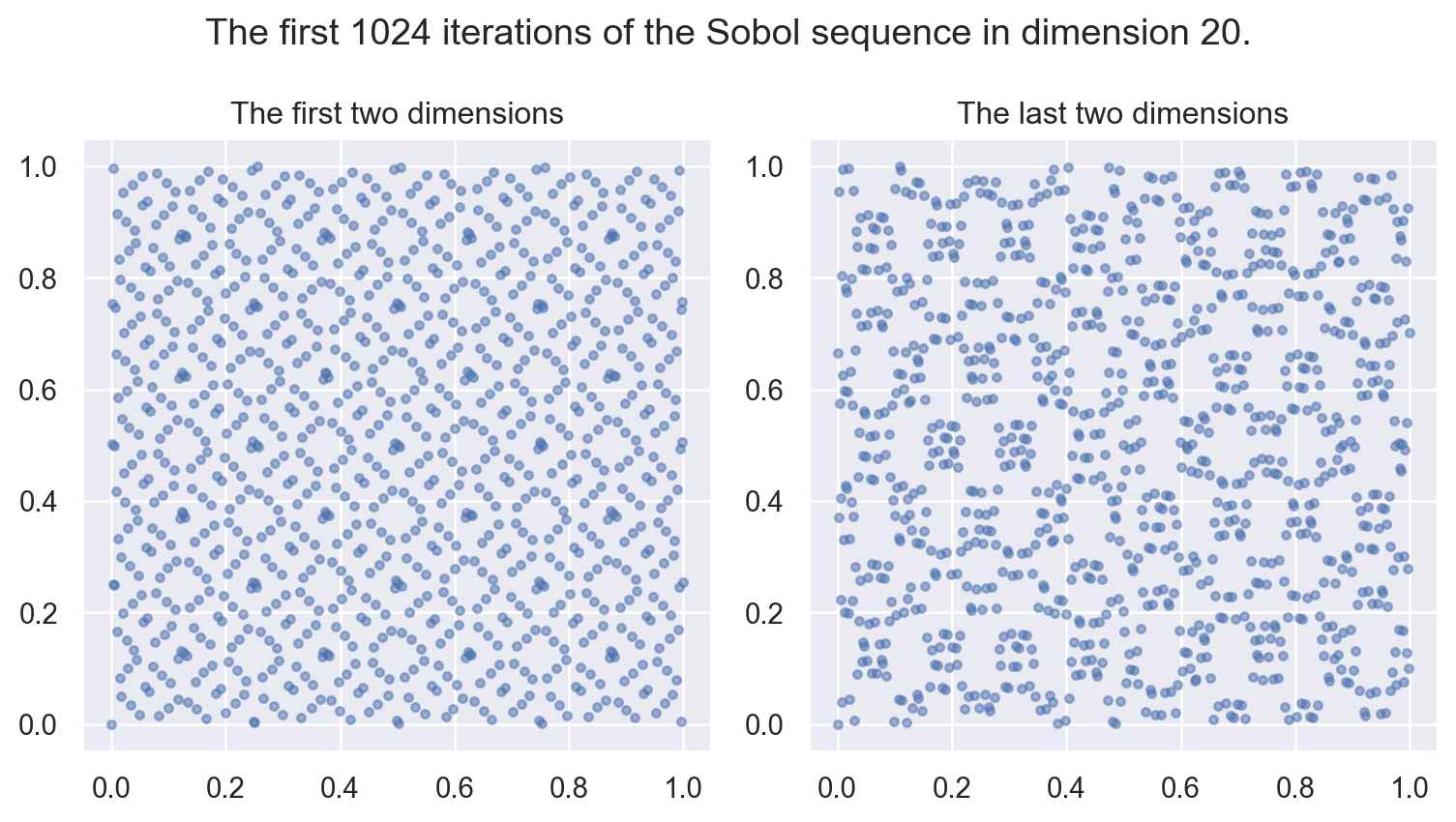

La même chose avec la version pertubée (option scramble=True activée par défaut).

n, d = 2**10, 20
sob = stats.qmc.Sobol(d=d, scramble=True)
sample = sob.random(n=n)

fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(8, 4.5), layout='tight')
ax1.scatter(sample[:,0], sample[:,1], s=10, marker='o', alpha=0.5)
ax1.set_title("The first two dimensions")
ax2.scatter(sample[:,-2], sample[:,-1], s=10, marker='o', alpha=0.5) 
ax2.set_title("The last two dimensions")
fig.suptitle(f"The first {n} iterations of the scrambled Sobol sequence in dimension {d}.")
plt.show()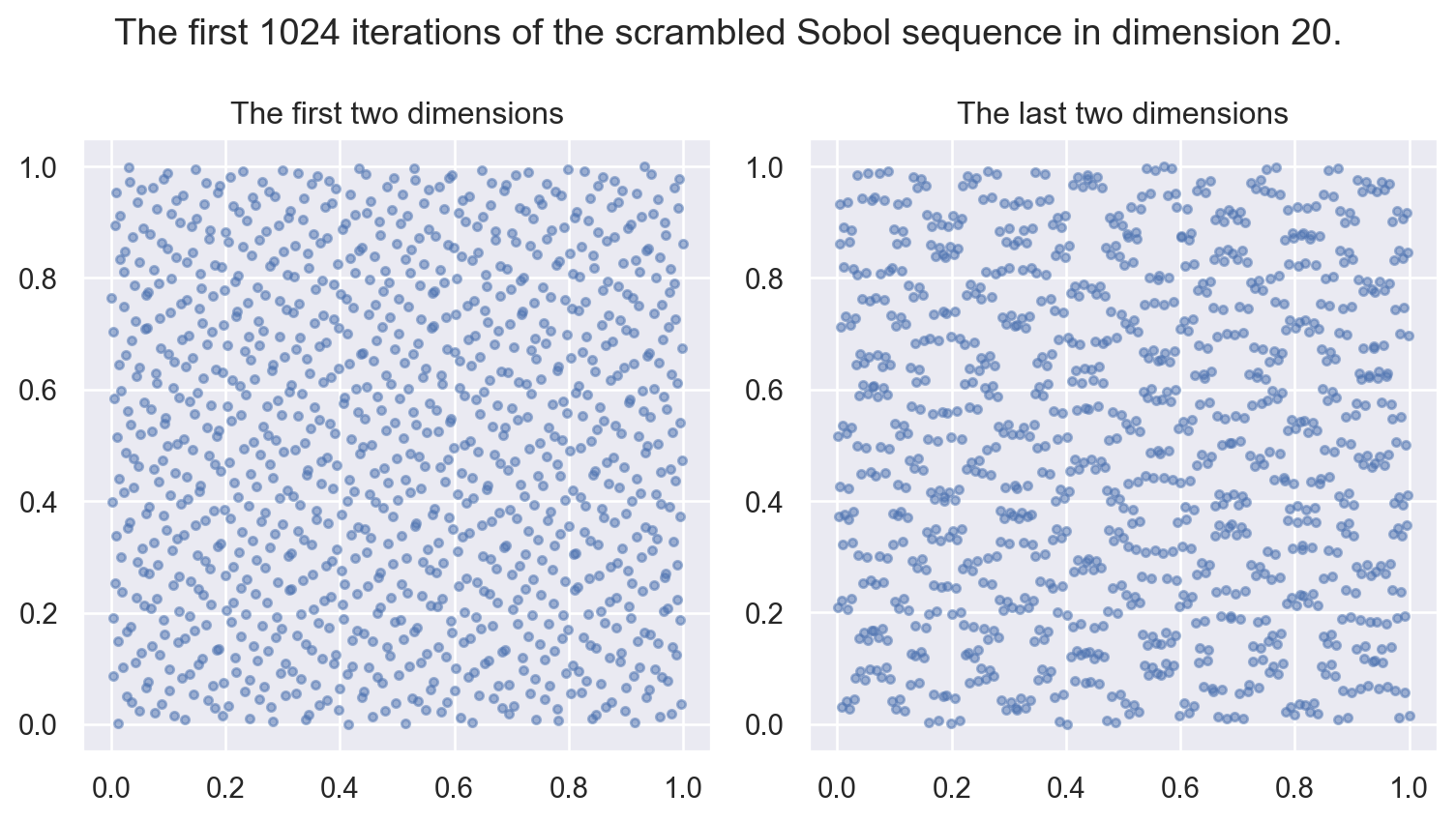

3.3 Intégration code C++ via pybind11

On a vu précédemment qu’il est possible d’écrire un code très proche du python qui sera compilé pour de meilleures performances: c’est le langage cython.

Une autre approche vient du projet pybind11. Imaginons qu’on dispose d’un code C++, une librairie écrite et optimisée en C++. Le projet pybind11 permet d’écrire assez facilement un module python qui permet d’accéder à ce code C++.

Nous allons illustrer l’utilisation de pybind11 pour interfacer (utiliser) la fonction sobol de la Gnu Scientific Library (code C orienté objet) dans un code python. Voici les différentes étapes:

• Comprendre la documentation de la section Quasi-Monte Carlo de la GSL
• Encapsuler ce code C dans un code objet C++ (pas obligatoire, mais permet de faire des rappels de C++)
• Utiliser pybind11 pour accéder à ce code C++

Note

Tout le code (que l’on va détailler) se trouve dans le répertoire sobol_module:

sobol_module
├── CMakeLists.txt
├── include
│   └── sobol.hpp
├── python
│   └── module.cpp
└── src
    └── test.cpp

• le fichier include/sobol.hpp contient le code de la “librairie” C++
• le fichier src/test.cpp contient un code C++ pour tester la “librairie” C++
• le fichier python/module.cpp contient le code C++ pour interfacer le C++ en python via pybind11.

3.3.1 Création d’une interface C++

Voici un code possible pour créer une classe sobol qui encapsule le code C de la GSL. On détaille le rôle des constructeurs, du destructeur, des opérateurs d’affectation et des 2 méthodes:

• la surcharge de l’opérateur fonctionnel operator()
• la méthode get

include/sobol.hpp

#pragma once

#include <vector>
#include <gsl/gsl_qrng.h>

class sobol {
    public:
        sobol(int dimension) : dimension(dimension) {
            q = gsl_qrng_alloc(gsl_qrng_sobol, dimension); }
        sobol(sobol const & o) : dimension(o.dimension) {
            q = gsl_qrng_clone(o.q); }
        sobol(sobol && o) = default;
        sobol & operator=(sobol const & o);
        sobol & operator=(sobol && o) = default;
        ~sobol() { gsl_qrng_free(q); }

        auto operator()();
        void get(double * data) { gsl_qrng_get(q, data); }

    private:
        int dimension;
        gsl_qrng * q;
};

sobol & sobol::operator=(sobol const & o) {
    if (this != &o) {
        dimension = o.dimension;
        gsl_qrng_memcpy(q, o.q);
    }
    return *this;
};

auto sobol::operator()() {
    std::vector<double> result(this->dimension);
    gsl_qrng_get(q, &(*result.begin()));
    return result;
};

Voici un exemple d’utilisation de cette classe. Le fichier src/test.cpp doit être compilé sans erreur.

src/test.cpp

#include <iostream>
#include "sobol.hpp"

using namespace std;
int main() {
    int d = 2;
    sobol S(d);

    for (int n = 0; n < 1e2; ++n) {
        auto xi_n = S();
        cout << n << ":\t" << xi_n[0] << "\t" << xi_n[1] << endl;
    }

    return 0;
}

Pour compiler ce code (via cmake et make) on peut utiliser le fichier CMakeLists.txt suivant:

CMakeLists.txt

cmake_minimum_required(VERSION 3.9)
set(CMAKE_VERBOSE_MAKEFILE ON)

project(sobol_module LANGUAGES CXX)

set(CMAKE_CXX_STANDARD 17)
set(CMAKE_CXX_STANDARD_REQUIRED ON)
set(CMAKE_CXX_EXTENSIONS OFF)
set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -Wall -Os -ffast-math")
set(CMAKE_MODULE_LINKER_FLAGS "-Wl,-w")

include_directories("${CMAKE_SOURCE_DIR}/include")

find_package(GSL REQUIRED)
include_directories(${GSL_INCLUDE_DIRS} ${GSLCBLAS_INCLUDE_DIRS})
set(LIBS ${LIBS} ${GSL_LIBRARIES} ${GSLCBLAS_LIBRARIES})

add_executable(sobol_test src/test.cpp)
target_link_libraries(sobol_test ${LIBS})

L’outil cmake est utilisé pour produire un fichier Makefile compatible avec l’OS et l’environnement installé. Le fichier Makefile étant produit, on utiliser l’outil make pour effectivement compiler le code (avec les bonnes librairies). Les étapes usuelles sont:

mkdir build    # on crée le répertoire vide (contenu de la compilation)
cd build       
cmake ..       # on appelle cmake sur `CMakeLists.txt` du répertoire père
make           # on appelle make pour la compilation 

Pour garder que les sources, on détruit le répertoire build (dont le contenu est propre à chaque environnement/ordinateur).

3.3.2 Intégration via pybind11

On consulte la documentation de ce module. Un premier exemple est donné ci-dessous:

#include <pybind11/pybind11.h>

int add(int i, int j) {
    return i + j;
}

PYBIND11_MODULE(example, m) {
    m.doc() = "pybind11 example plugin"; // optional module docstring

    m.def("add", &add, "A function which adds two numbers",
      py::arg("i"), py::arg("j"));
}

Le code PYBIND11_MODULE est une macro C/C++ qui permet la création d’un module python dont le nom est example et le contenu est m (m est un objet dont on va définir des méthodes). Dans l’exemple précédent m.doc() permet de définir une documentation et m.def ajoute dans le module python une fonction add dont le code de la fonction C++ se trouve à l’adresse &add.

Ici on va utiliser un code un peu plus riche et on fait appel à pybind11/numpy.h pour manipuler des array numpy dans notre code C++. Pour plus d’information voir la documentation.

Le module créé s’appelle sobol_module. Dans ce module se trouve une fonction sobol et le code est donné par une lambda function qui prend 2 arguments n et dim et renvoie un array de dimension (n, dim) qui contient les n premiers termes de la suite de Sobol en dimension dim.

python/module.cpp

#include <pybind11/pybind11.h>
#include <pybind11/numpy.h>
#include <pybind11/stl.h>
#include "sobol.hpp"

namespace py = pybind11;

PYBIND11_MODULE(sobol_module, m) {
    m.doc() = "Sobol GSL module integrated via pybind11"; 
    m.def("sobol", [](int n, int dim) {
        sobol S(dim);
        auto result = py::array_t<double>(n * dim).reshape({ n, dim });
        auto buf = result.request();
        double * ptr = static_cast<double*>(buf.ptr);
        for (int k = 0; k < n; ++k) {
            S.get(ptr);
            ptr += dim;
        }
        return result;
    });
}

Note

Pour la compilation il suffit de modifier le fichier CMakeLists et d’ajouter les lignes suivantes (on suppose que pybind11 est bien installé).

CMakeLists.txt

find_package(Python 3.11 EXACT COMPONENTS Interpreter Development)
find_package(pybind11 CONFIG REQUIRED)
pybind11_add_module(sobol_module python/module.cpp) 
target_link_libraries(sobol_module PUBLIC GSL::gsl GSL::gslcblas)

Dans le répertoire sobol_module se trouve maintenant le sous-répertoire build qui contient sobol_module.cpython-311-darwin.so une librairie (module) qui peut être chargé pour utilisé la fonction sobol. Un appel possible est le suivant

%cd sobol_module/build/
from sobol_module import sobol 

sobol(20, 5)

array([[0.5    , 0.5    , 0.5    , 0.5    , 0.5    ],
       [0.75   , 0.25   , 0.75   , 0.25   , 0.75   ],
       [0.25   , 0.75   , 0.25   , 0.75   , 0.25   ],
       [0.375  , 0.375  , 0.625  , 0.125  , 0.875  ],
       [0.875  , 0.875  , 0.125  , 0.625  , 0.375  ],
       [0.625  , 0.125  , 0.375  , 0.375  , 0.125  ],
       [0.125  , 0.625  , 0.875  , 0.875  , 0.625  ],
       [0.1875 , 0.3125 , 0.3125 , 0.6875 , 0.5625 ],
       [0.6875 , 0.8125 , 0.8125 , 0.1875 , 0.0625 ],
       [0.9375 , 0.0625 , 0.5625 , 0.9375 , 0.3125 ],
       [0.4375 , 0.5625 , 0.0625 , 0.4375 , 0.8125 ],
       [0.3125 , 0.1875 , 0.9375 , 0.5625 , 0.4375 ],
       [0.8125 , 0.6875 , 0.4375 , 0.0625 , 0.9375 ],
       [0.5625 , 0.4375 , 0.1875 , 0.8125 , 0.6875 ],
       [0.0625 , 0.9375 , 0.6875 , 0.3125 , 0.1875 ],
       [0.09375, 0.46875, 0.84375, 0.40625, 0.28125],
       [0.59375, 0.96875, 0.34375, 0.90625, 0.78125],
       [0.84375, 0.21875, 0.09375, 0.15625, 0.53125],
       [0.34375, 0.71875, 0.59375, 0.65625, 0.03125],
       [0.46875, 0.09375, 0.46875, 0.28125, 0.65625]])

%timeit sobol(1000000, 5)

3.23 ms ± 49.6 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)

Avertissement

Pour aller plus loin, il est possible d’intégrer une classe C++ en python via pybind11. Lire la documentation et appliquer à la classe sobol du fichier include/sobol.hpp.

3.4 Application aux options basket

On adapte le code de la séance précédente pour faire un code QMC et comparer avec le code MC.

%cd ../../
%run 02_basket.ipynb 

def monte_carlo_by_steps(sampling_function: callable, 
                         steps: np.ndarray,
                         proba: float = 0.95) -> dict:
    """
    Effectue une estimation de Monte Carlo par étapes successives et calcule 
    les intervalles de confiance pour la moyenne à chaque étape.

    Args:
    - sampling_function (callable): Fonction qui génère des échantillons.
    - steps (np.ndarray): Tableau des étapes successives.
    - proba (float): Niveau de confiance pour les intervalles de confiance.

    Returns:
    - dict: Un dictionnaire contenant les moyennes, les variances et 
    les intervalles de confiance pour chaque étape.
    """
    alpha = 1 - proba
    quantile = sps.norm.ppf(1 - alpha / 2)

    means = np.empty(len(steps))
    variances = np.empty(len(steps)) 
    prev_step = 0
    
    sum_, sum2_ = 0.0, 0.0
    for k, step in enumerate(steps):   
        samples = sampling_function(steps[k] - prev_step)
        sum_ += samples.sum()
        sum2_ += (samples**2).sum()
        
        means[k] = sum_ / step
        variances[k] = step / (step-1) * (sum2_ / step - means[k]**2)
        prev_step = steps[k]

    ci_sizes = 2 * quantile * np.sqrt(variances / steps)
    return {
        "steps": steps,
        "means": means,
        "variances": variances,
        "lowers": means - ci_sizes,
        "uppers": means + ci_sizes,
    }

K = 100
step_size = 100
steps = step_size + np.arange(0, 500000, step_size)
r_mc = monte_carlo_by_steps(
    lambda size: sampling_payoffs(K, size, bs, rng), 
    steps)

Note

Il suffit ici de modifier la fonction sampling_payoffs en remplaçant l’appel de

rng.standard_normal((size, bs["d"]))

par

stats.norm.ppf(qmc_algo.random(size))

où qmc_algo code une suite à discrépance faible sur \((0,1)^d\).

def qsampling_payoffs(K, size, bs, qmc_algo):
    Gn = stats.norm.ppf(qmc_algo.random(size))
    samples = phi(bs, Gn)
    payoffs = np.maximum(np.mean(samples, axis=1)-K, 0.) 
    return bs["actualization"] * payoffs

qmc_algos = {
    "halton": stats.qmc.Halton(d=d, scramble=False).fast_forward(1), 
    "halton_scrambled": stats.qmc.Halton(d=d, scramble=True).fast_forward(1), 
    "sobol": stats.qmc.Sobol(d=d, scramble=False).fast_forward(1),
    "sobol_scrambled": stats.qmc.Sobol(d=d, scramble=True).fast_forward(1)
}

Avertissement

On appelle la méthode fast_forward(k) pour démarrer à partir de l’itération \(k\). Ici on part à partir de l’itération \(k=1\) pour supprimer le point \(0 \in [0,1]^d\) qui pose problème lors de l’appel de stats.norm.ppf !

En pratique on remarque qu’on peut avoir une convergence plus rapide pour Halton en supprimant les premières itérations.

r_qmc = { 
    name: monte_carlo_by_steps(
        lambda size: qsampling_payoffs(K, size, bs, algo),
        steps)
    for name, algo in qmc_algos.items() 
}

fig, (ax1, ax2) = plt.subplots(figsize=(8, 4), ncols=2, nrows=1, 
                               sharey=True, layout='tight')

ax1.plot(steps, r_qmc["halton"]["means"], label="Halton QMC est.")
ax1.plot(steps, r_qmc["sobol"]["means"], label="Sobol QMC est.")
ax2.plot(steps, r_qmc["halton_scrambled"]["means"], label="Halton RQMC est.")
ax2.plot(steps, r_qmc["sobol_scrambled"]["means"], label="Sobol RQMC est.")
for ax in (ax1, ax2): 
    ax.plot(steps, r_mc["means"], label="MC estimator")
    ax.fill_between(steps, r_mc["lowers"], r_mc["uppers"], 
                    facecolor='lightyellow', label="MC 95% CI")
    ax.set_ylim([12.05, 12.45])
    ax.legend(loc='lower right')
plt.show()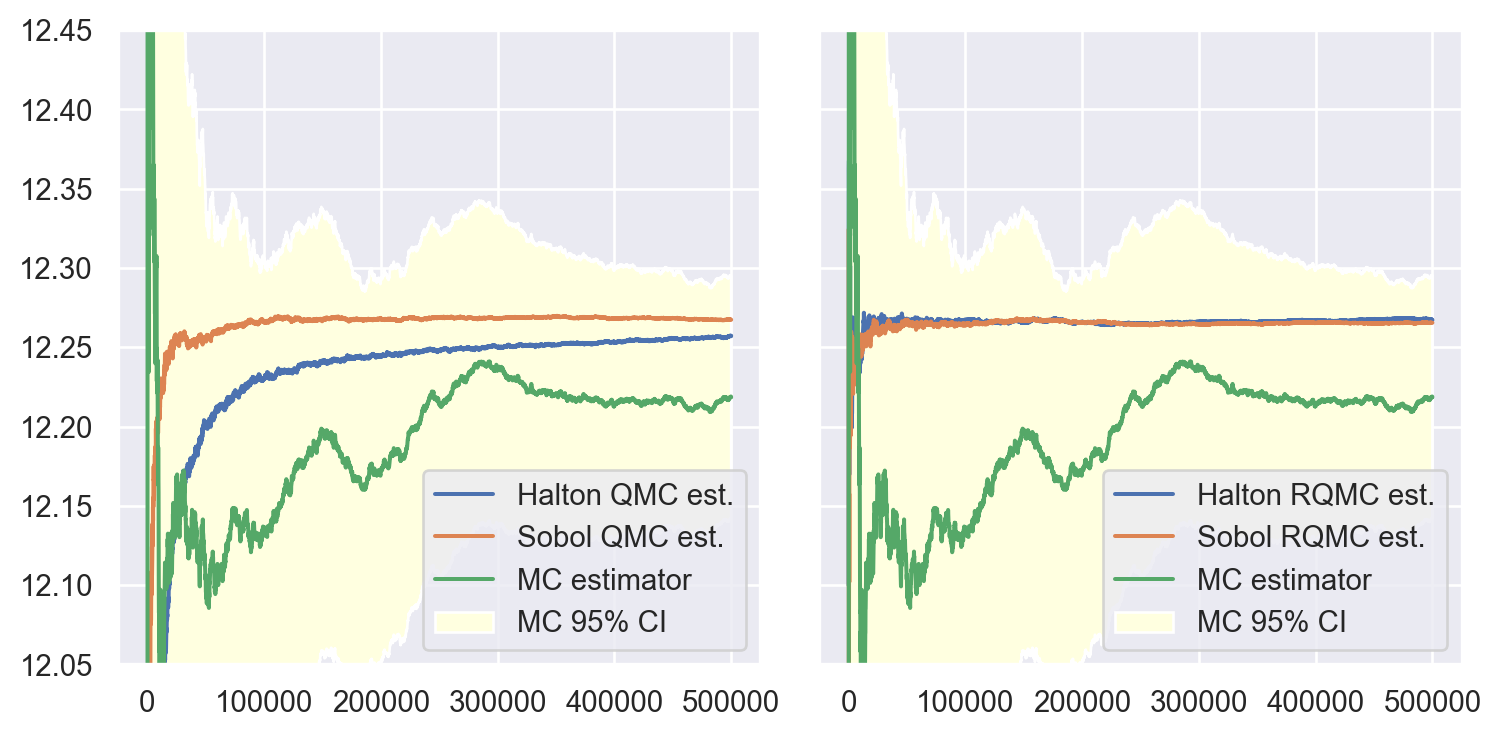

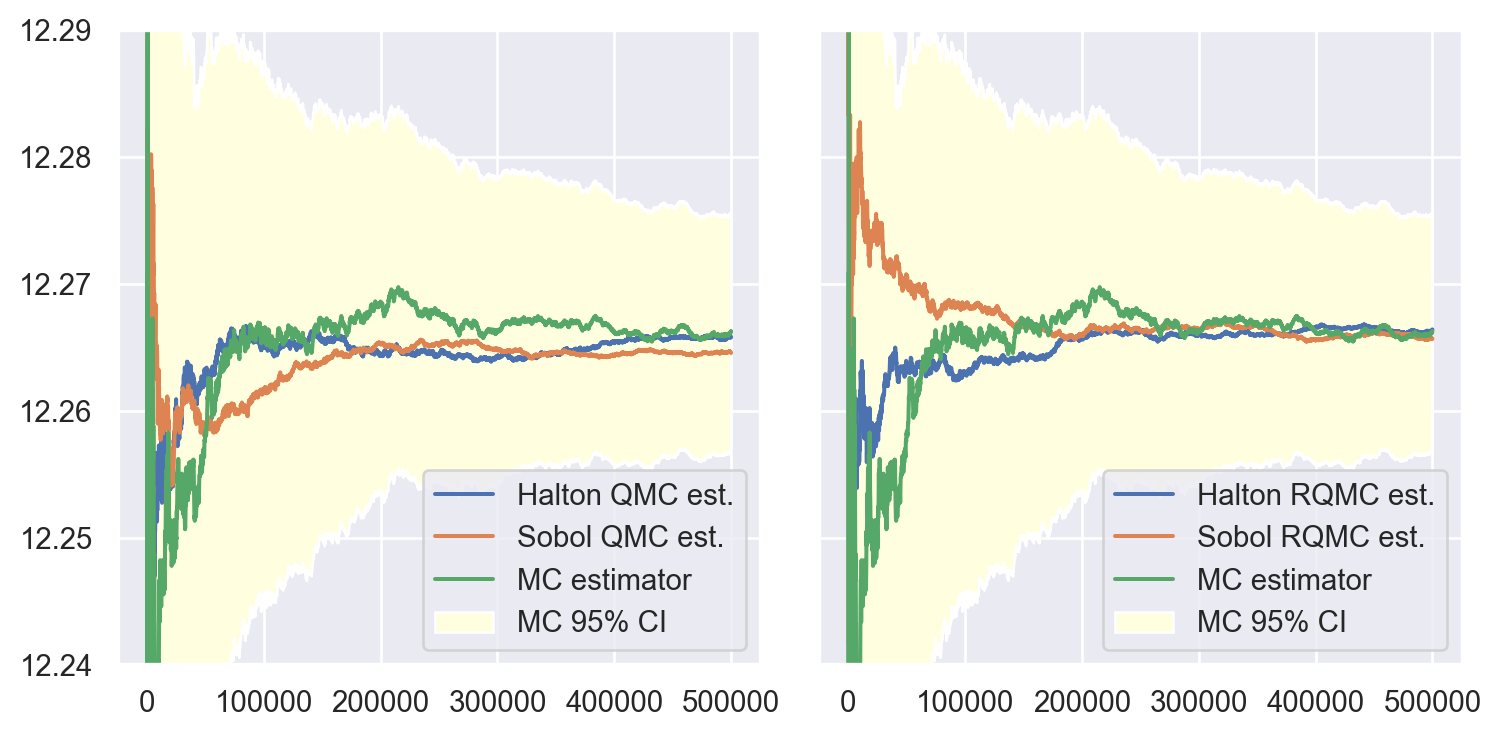
3.4.1 Avec variable de contrôle

def qsampling_payoffs_control_variate(K, size, bs, qmc_algo):
    Gn = stats.norm.ppf(qmc_algo.random(size))
    payoffs_X = np.maximum(np.mean(phi(bs, Gn), axis=1) - K, 0) 
    payoffs_Y = payoffs_control(bs, K, Gn)
    payoffs = payoffs_X - payoffs_Y
    return bs["actualization"] * payoffs

r_mc = monte_carlo_by_steps(
    lambda size: sampling_payoffs_control_variate(K, size, bs, rng), 
    steps)
r_qmc = { 
    name: monte_carlo_by_steps(
        lambda size: qsampling_payoffs_control_variate(K, size, bs, algo),
        steps)
    for name, algo in qmc_algos.items() 
}
fig, (ax1, ax2) = plt.subplots(figsize=(8, 4), ncols=2, nrows=1, 
                               sharey=True, layout='tight')

ax1.plot(steps, r_qmc["halton"]["means"], label="Halton QMC est.")
ax1.plot(steps, r_qmc["sobol"]["means"], label="Sobol QMC est.")
ax2.plot(steps, r_qmc["halton_scrambled"]["means"], label="Halton RQMC est.")
ax2.plot(steps, r_qmc["sobol_scrambled"]["means"], label="Sobol RQMC est.")
for ax in (ax1, ax2): 
    ax.plot(steps, r_mc["means"], label="MC estimator")
    ax.fill_between(steps, r_mc["lowers"], r_mc["uppers"], 
                    facecolor='lightyellow', label="MC 95% CI")
    ax.set_ylim([12.24, 12.29])
    ax.legend(loc='lower right')
plt.show()