1.10. Exemple: marche aléatoire symétrique sur \(\mathbf{Z}\)

On considère la chaine de Markov sur \(\mathbf{Z}\) définie par la probabilité de transition \(P\)

\[\begin{equation*} \forall x \in \mathbf{Z}, \quad P(x, x+1) = P(x, x-1) = \frac{1}{2}, \end{equation*}\]

et l’état initial \(0\).

L’écriture dynamique de cette chaine est la suite \((X_n)_{n \ge 0}\) définie par

\[\begin{equation*} \forall n \ge 0, \quad X_{n+1} = X_n + \xi_{n+1}, \end{equation*}\]

avec \(X_0 = 0\) et \((\xi_n)_{n \ge 1}\) une suite i.i.d. à valeurs dans \(\{-1,1\}\) telle que \(\mathbf{P}(\xi_1 = 1) = \mathbf{P}(\xi_1 = -1) = \frac{1}{2}\).

n_steps = 1001
n_paths = 100000
sample = np.empty((n_steps, n_paths))

On veut simuler \(100\,000\) trajectoires sur \(1\,000\) itérations. La matrice globale qui contient toutes les trajectoires est stockée dans la variable sample. Dans la mesure du possible on écrit un code pour simuler toutes les trajectoires simultanément: on aura une seule boucle for sur le nombre d’itérations.

sample[0] = 0
for n in range(1, n_steps):
    xi = 2*rng.integers(2, size=n_paths) - 1
    sample[n] = sample[n-1] + xi

fig, ax = plt.subplots(layout='tight')
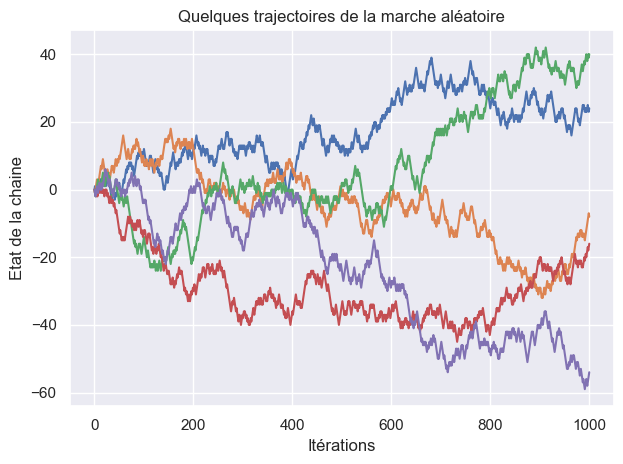
ax.plot(np.arange(n_steps), sample[:,:5])
ax.set_ylabel('Etat de la chaine')
ax.set_xlabel('Itérations')
ax.set_title('Quelques trajectoires de la marche aléatoire')
plt.show()

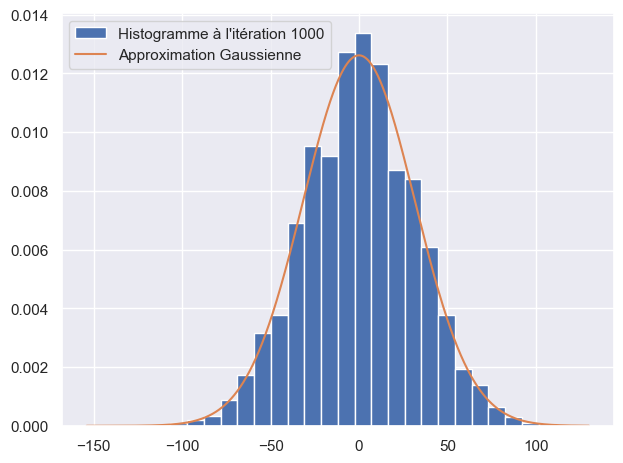
La loi terminale \(X_n\) est distribuée selon une loi binomiale recentrée que l’on peut approcher (pour \(n\) grand) par une loi normale de variance \(n\). On utilise ce résultat pour vérifier la validité du code et des simulations.

xx = np.linspace(min(sample[-1]), max(sample[-1]), 5000)
yy = stats.norm.pdf(xx, scale=np.sqrt((n_steps-1)))

fig, ax = plt.subplots(layout='tight')
ax.hist(sample[-1], bins=30, density=True, label=f"Histogramme à l'itération {n_steps-1}")
ax.plot(xx, yy, label="Approximation Gaussienne")
ax.legend()
plt.show()

1.10.1. Optimisation du code

Dans ce cas très particulier de la marche aléatoire, on peut éviter la boucle for sur les itérations et remplacer cette boucle par un appel de la fonction np.cumsum. Cette somme cumulée est très utilisée pour tous les processus à accroissements indépendants: on reconstruit le processus à partir de la somme cumulée des accroissements.

sample = np.empty((n_steps, n_paths))
sample[0] = 0
acc_sample = 2*rng.integers(2, size=(n_steps-1, n_paths))-1
sample[1:] = np.cumsum(acc_sample, axis=0)