2.8. Exemple numérique: MC avec variable de contrôle

On considère le calcul de \(I = \mathbf{E} \Big[\cos\big(\frac{\pi}{2} U\big) \Big]\) où \(U \sim \mathcal{U}(]0,1[)\).

On commence par tracer la fonction \(f\) sur \([0,1]\), ainsi que 2 approximations naturelles, la fonction linéaire \(u \mapsto 1-u\) et la fonction quadratique \(u \mapsto 1-u^2\) qui valent toutes les deux 1 en \(u=0\) et 0 en \(u=1\).

from math import pi
def f(u):
    return np.cos(0.5*pi*u)
uu = np.linspace(0, 1, 1000)

fig, ax = plt.subplots(layout='tight')
ax.plot(uu, f(uu), label=r"$f:u \mapsto \cos(\frac{\pi}{2} u)$")
ax.plot(uu, 1-uu, label=r"$u \mapsto 1-u$")
ax.plot(uu, 1-uu*uu, label=r"$u \mapsto 1-u^2$")
ax.set_title(r"Comparaison de deux approximations de la fonction $f$ sur $[0,1]$")
ax.legend()
plt.show()

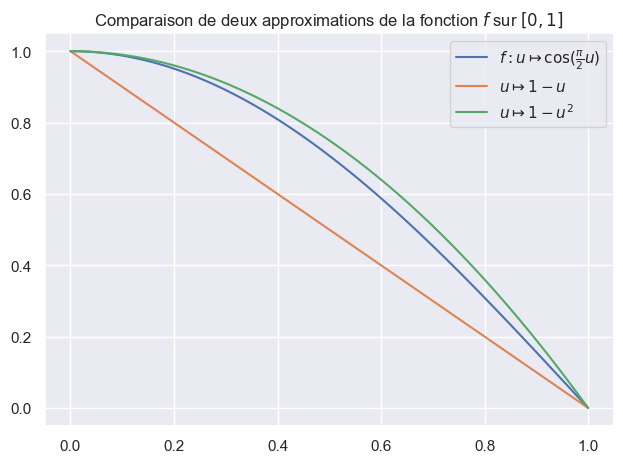
On suppose que l’on connait \(\mathbf{E}[U] = \frac{1}{2}\) et \(\mathbf{E}[U^2] = \frac{1}{3}\). De sorte que \(\mathbf{E}[1-U] = \frac{1}{2}\) et \(\mathbf{E}[1-U^2] = \frac{2}{3}\).

Ces approximations suggèrent d’utiliser et de comparer les variables de contrôles (recentrées) suivantes:

\[\begin{equation*} Y^{(1)} = \frac{1}{2} - U, \quad \text{et} \quad Y^{(2)} = \frac{1}{3} - U^2. \end{equation*}\]

On a donc deux représentations de \(I\)

\[\begin{equation*} I = \mathbf{E} \Big[ \cos\big(\frac{\pi}{2} U\big) - \big(\frac{1}{2}-U\big) \Big] = \mathbf{E} \Big[ \cos\big(\frac{\pi}{2} U\big) - \big(\frac{1}{3}-U^2\big) \Big] \end{equation*}\]

où \(U \sim \mathcal{U}(]0,1[)\), ce qui conduit à deux estimateurs différents

\[\begin{align*} I_n^{(1)} &= \frac{1}{n} \sum_{k=1}^n \Big( \cos\big(\frac{\pi}{2} U_k\big) - \big(\frac{1}{2}-U_k\big) \Big), \\ I_n^{(2)} &= \frac{1}{n} \sum_{k=1}^n \Big( \cos\big(\frac{\pi}{2} U_k\big) - \big(\frac{1}{3}-U_k^2\big) \Big). \end{align*}\]

où \((U_k)_{k \ge 1}\) suite i.i.d. uniforme sur \(]0,1[\).

Show code cell source Hide code cell source

from scipy import stats

def monte_carlo(sample, proba = 0.95):
    """
    Computes the mean, variance, and a confidence interval (CI) of a 
    given sample data set using the Monte Carlo method.
    Parameters:
    -----------
    sample : array-like
        The data set to be analyzed
    proba : float, optional
        The probability that the true mean of the population is 
        within the calculated interval. Default is 0.95
    Returns:
    --------
    dict of { 'mean': float, 'var': float, 'lower': float, 'upper': float } 
        The mean, variance, lower bound of the CI and upper bound of the CI
    """
    mean = np.mean(sample)
    var = np.var(sample, ddof=1)
    alpha = 1 - proba 
    quantile = stats.norm.ppf(1 - alpha/2)  # fonction quantile 
    ci_size = quantile * np.sqrt(var / sample.size)
    result = { 'mean': mean, 'var': var, 
               'lower': mean - ci_size, 
               'upper': mean + ci_size }
    return result

n = int(1e5)
sample_U = rng.random(size=n)
sample_mc = f(sample_U)
sample_vc1 = f(sample_U) - (0.5 - sample_U)
sample_vc2 = f(sample_U) - (1./3. - sample_U**2)
result = pd.DataFrame([ 
    monte_carlo(sample) for sample in [sample_mc, sample_vc1, sample_vc2] ],
    index = ["MC", "VC1", "VC2"])
result

	mean	var	lower	upper
MC	0.636764	0.094798	0.634855	0.638672
VC1	0.636665	0.004105	0.636267	0.637062
VC2	0.636652	0.000381	0.636531	0.636773

ratio_1 = result["var"]["MC"] / result["var"]["VC1"]
ratio_2 = result["var"]["MC"] / result["var"]["VC2"]
print("Le ratio de variance par la première variable de contrôle:", ratio_1)
print("Le ratio de variance par la seconde variable de contrôle:", ratio_2)

Le ratio de variance par la première variable de contrôle: 23.090634291197823
Le ratio de variance par la seconde variable de contrôle: 248.7490197397456