7.3 Algorithme EM

L’algorithme EM ou Expectation-Maximization algorithm de Dempster, Laird, and Rubin (1977) est une procédure itérative pour approcher l’estimateur du maximum de vraisemblance lorsque celui n’admet pas d’expression explicite. Il est particulièrement appropriée pour des nombreux modèles à variables latentes.

Supposons que l’on ait un modèle à variables manquantes avec des observations \(\mathbf X=(X_i)_{1\le i\le n}\), aussi appelées données incomplètes, et des variables latentes ou manquantes \(\mathbf Z=(Z_i)_{1\le i\le n}\). On appelle données complètes l’ensemble des variables \((\mathbf Z,\mathbf X)\).

Bien que la vraisemblance \(\mathcal L(\theta)\), aussi dite vraisemblance des données incomplètes, ne soit pas calculable efficacement, la vraisemblance des données complètes \(\mathbb P_{\theta}(\mathbf Z,\mathbf X)\) est simple et facile à manipuler dans la grande majorité de modèles. L’idée de l’algorithme EM consiste alors à utiliser la (log-)vraisemblance des données complètes pour approcher la (log-)vraisemblance observée \(\log\mathcal L(\theta)\) en prenant l’espérance de la première. Ainsi, on introduit la quantité suivante \[\begin{equation} \tag{7.1} Q(\theta, \theta') =\mathbb E_{\theta'}[\log \mathbb P_{\theta}(\mathbf Z,\mathbf x)|\mathbf X=\mathbf x]. \end{equation}\] En notant \(\theta^*\) la vraie valeur du paramètre, \(Q(\theta, \theta^*)\) approche la log-vraisemblance des données incomplètes et donc l’estimateur de maximum de vraisemblance peut être approché par le maximum de \(\theta\mapsto Q(\theta, \theta^*)\). Or, la vraie valeur du paramètre \(\theta^*\) étant inconnue, il faut procéder autrement. L’algorithme EM consiste à alterner l’évaluation de \(Q(\theta, \theta')\) (E-step) et sa maximisation en \(\theta\) (M-step) jusqu’à convergence.

Algorithme. Expectation-Maximization algorithm.

Entrée: des observations \(\mathbf x\), la distribution du modèle (pour le calcul de \(Q(\theta, \theta')\)), une valeur initiale \(\theta^0\) du paramètre

Sortie: paramètre \(\theta^k\)

Procédure: A l’itération \(k\), on effectue les deux étapes suivatens:

  • E-step: on calcule \(\theta\mapsto Q(\theta, \theta^{k-1})\) où \(Q\) est défini en (7.1).

  • M-step: on maximise \(\theta^{k}=\arg\max_{\theta}Q(\theta,\theta^{k-1})\).

On arrête lorsqu’un nombre maximum d’itérations est atteint ou \(\|\theta^{k+1}-\theta^k\|/\|\theta^k\| \le \varepsilon\) ou un nombre maximum d’itérations est atteint ou si \(|Q(\theta^k,\theta^{k-1})-Q(\theta^{k-1},\theta^{k-2})|\le\varepsilon\).

L’algorithme EM à la propriété importante de toujours augementer la vraisemblance observée.
Theorem 7.1 A chaque itération de l’algorithme EM, la vraisemblance observée \(\mathcal L\) augmente, à savoir \[\mathcal L(\theta^{k+1})\geq\mathcal L(\theta^{k}),\qquad\text{pour tout } k\geq1.\]
Proof. A chaque itération, la vraisemblance observée augmente. En effet, par construction on sait que \(Q(\theta^{k+1},\theta^k) \ge Q(\theta^k,\theta^k)\), i.e. \[\begin{align*} 0 &\le Q(\theta^{k+1},\theta^k) - Q(\theta^k,\theta^k)\\ &= \mathbb E_{\theta^k}\left[\log \frac{\mathbb P_{\theta^{k+1}}(\mathbf Z,\mathbf x)} {\mathbb P_{\theta^{k}}(\mathbf Z,\mathbf x)} \Big| \mathbf X=\mathbf x \right]\\ & \mathop{\le}_{ \textrm{Ineg. Jensen}} \log \mathbb E_{\theta^k} \left[ \frac{\mathbb P_{\theta^{k+1}}(\mathbf Z,\mathbf x)} {\mathbb P_{\theta^{k}}(\mathbf Z,\mathbf x)} \Big| \mathbf X=\mathbf x \right] \\ &= \log \int_{\mathcal{Z}^n} \frac{\mathbb P_{\theta^{k+1}}(\mathbf z,\mathbf x)} {\mathbb P_{\theta^{k}}(\mathbf z,\mathbf x)} \mathbb P_{\theta^{k}}(\mathbf z|\mathbf X=\mathbf x) ds_1\ldots ds_n \\ &= \log \int_{\mathcal{Z}^n} \frac{\mathbb P_{\theta^{k+1}}(\mathbf z,\mathbf x)} {\mathbb P_{\theta^{k}}(\mathbf x)} ds_1\ldots ds_n \\ &= \log \frac{\mathbb P_{\theta^{k+1}}(\mathbf x)} {\mathbb P_{\theta^{k}}(\mathbf x)}\\ &= \log(\mathcal L(\theta^{k+1}))-\log(\mathcal L(\theta^{k})). \end{align*}\] D’où \(\mathcal L(\theta^{k+1})\geq\mathcal L(\theta^{k})\).

 

Théorème 7.1 ne donne pas de garantie que l’algorithme EM converge vers le maximum global. Néanmoins, sous des hypothèses assez générales, on peut montrer que l’algorithme EM converge toujours vers un point critique de la vraisemblance. Au fait, le choix du point initial \(\theta^0\) est crucial, car l’algorithme EM est une procédure déterministe. En pratique, on lance l’algorithme plusieurs fois avec différentes initialisations en espérant de trouver ainsi le maximum global.

Interprétation géométrique de l’algorithme EM L’algorithme EM fait partie de la famille des MM algorithms (MM pour majorize-minimize ou minorize-maximize). L’idée est simple: comme il est difficile de maximiser directement la log-vraisemblance des données incomplètes \(\ell(\theta):=\log(\mathcal L(\theta))\), on cherche un fonction (surrogate function) qui est un borne inférieure de \(\ell(\theta)\) et tangente à \(\ell(\theta)\) en un point connu, typiquement en le point actuel \(\theta^k\) du l’algorithme itératif. Au lieu de maximiser \(\ell(\theta)\), on maximise alors la borne inférieure, cf. Figure @fig:figPrincipeEM.

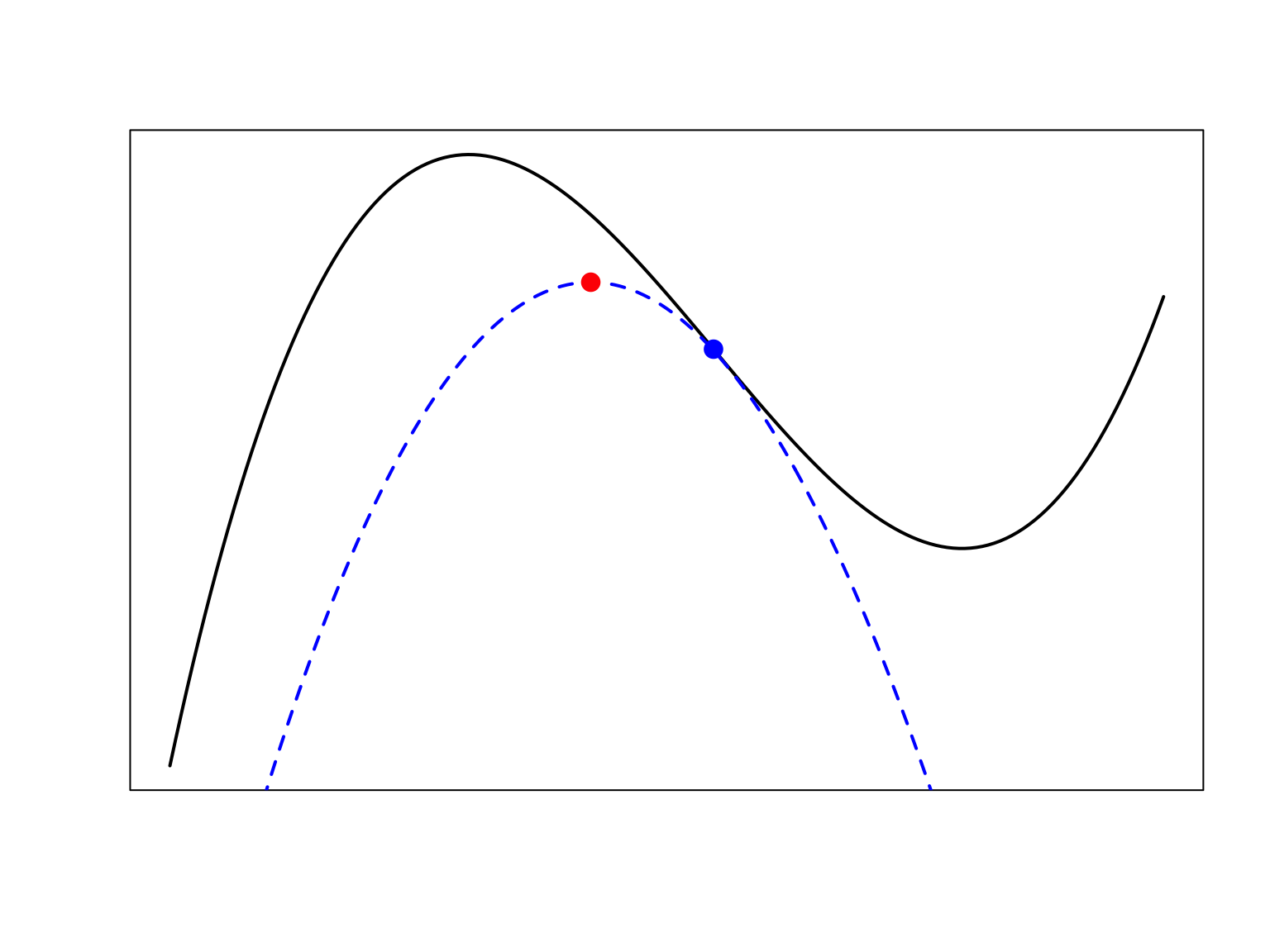
En noir la fonction à maximiser, en bleu une borne inférieure qui est égale à la fonction noir en le point bleu qui est la valeur actuelle de l’algorithme. En maximisant la fonction bleue on trouve le point rouge. En le point rouge la valeur de la fonction noire est supérieure qu’en le point bleu. On itère: maintenant il faut calculer la borne inférieure qui touche la fonction noire en le point rouge etc.

Figure 7.1: En noir la fonction à maximiser, en bleu une borne inférieure qui est égale à la fonction noir en le point bleu qui est la valeur actuelle de l’algorithme. En maximisant la fonction bleue on trouve le point rouge. En le point rouge la valeur de la fonction noire est supérieure qu’en le point bleu. On itère: maintenant il faut calculer la borne inférieure qui touche la fonction noire en le point rouge etc.

Plus précisément, pour l’algorithme EM, on peut montrer que pour tout \(\theta^k\) il existe une constante \(\kappa\) telle que

  1. \(Q(\theta,\theta^k)+\kappa \leq \ell(\theta)\) pour tout \(\theta\).

  2. \(Q(\theta^k,\theta^k)+\kappa = \ell(\theta^k)\).

Variante de l’algorithme EM Lorsque la maximisation de \(\theta\mapsto Q(\theta,\theta^k)\) est difficile aussi, on remplace le M-step par la recherche d’un point \(\theta^{k+1}\) qui somplement augmente la valeur de \(Q(\theta,\theta^{k})\), i.e. \(Q(\theta^{k+1}, \theta^{k})\geq Q(\theta^{k},\theta^{k})\). Pour cela, on peut par exemple effectuer une étape de l’algorithme de Newton-Raphson. Dans cette variante de l’algorithme EM, on a aussi la propriété que la suite \(\left(\ell(\theta^k)\right)_{k\geq1}\) est croissante.

Remarques

Dans de nombreux modèles les deux étapes, E-step et M-step, ont des expressions explicites comme dans le modèle de mélange gaussien. De manière simplifiée, on peut dire que le M-step est explicite, si la maximisation de la vraisemblance complètes l’est. Par exemple, pour un mélange gaussien le M-step est explicite, car l’estimateur de maximum de vraisemblance de la loi gaussienne est explicite.

Cependant, l’étape E de l’algorithme requiert de pouvoir calculer facilement la loi conditionnelle des variables latentes \(\mathbf Z\) sachant les observations \(\mathbf X\). C’est le cas par exemple pour les modèles de mélange finis où la loi aposteriori de \(\mathbf Z\) se factorise. Mais il y a d’autres modèles où la loi conditionnelle de \(\mathbf Z\) est intractable et donc le E-step n’est pas faisable.

Dans la prochaine section, nous verrons un outil pratique pour analyser la structure de dépendance entre les variables d’un modèle et notamment des lois conditionnelles. Il s’agit des modèles graphiques.

References

Dempster, A. P., N. M. Laird, and D. B. Rubin. 1977. “Maximum Likelihood from Incomplete Data via the EM Algorithm.” J. Roy. Statist. Soc. Ser. B 39 (1): 1–38.