2.1 Densité

Nous avons déjà introduit l’ordre et la taille d’un graphe \(G=(V,E)\), cf. 1.2. Ce sont clairement les caractéristiques les plus simples d’un graphe. Pourtant, parfois rien que l’évolution de l’ordre du graphe peut être intéressant comme l’illustre la Figure 2.1.

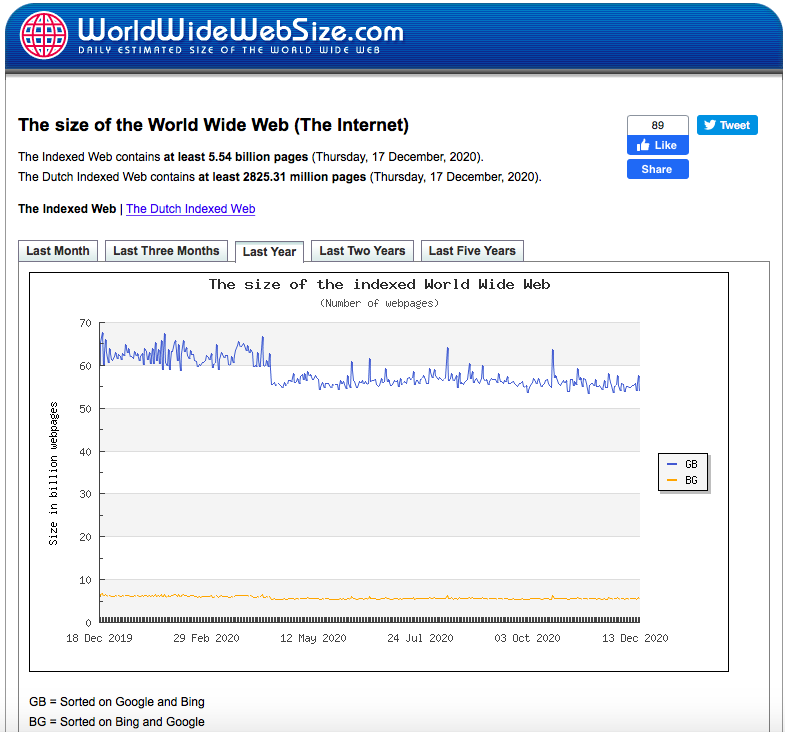
Figure 2.1: L’évolution de l’ordre du World Wide Web en 2020.

En combinant les notions taille et ordre d’un graphe, on définit sa densité.

Definition 2.1 La densité d’un graphe \(G=(V,E)\) est définie par \[ \text{den}(G)=\frac {|E|}{|V|(|V|-1)/2}. \]

La densité, comprise entre 0 et 1, traduit à quel point les noeuds sont connectés ou pas. Plus la densité est proche de 1, plus le graphe ressemble à un graphe complet où chaque noeud est connectés à tous les autres noeuds.

Definition 2.2 Le graphe complet ou une clique \(K_n\) est le graphe non dirigé sur \(n\) sommets qui contient toutes les arêtes possibles entre ces sommets.

Ainsi, \(K_2\) est une simple arête entre deux noeuds, \(K_3\) est un triangle. Les sous-graphes complets d’un graphe sont plus communément appelés cliques.

Etant une quantité normalisée, la densité permet de comparer des graphes d’ordres différents entre eux.

On peut définir une densité locale en considérant un sous-graphe \(H\subset G\).