4.6 TP - Graphes de similarités

Dans ce TP, nous analysons l’effet du choix du graphe de similarité ainsi que l’effet du choix de la méthode sur le clustering obtenu.

Nous simulons un jeu de données de \(n = 100\) points \(x_i\) dans \(\mathbb R^2\) par les instructions suivantes:

library(mlbench)
n=100
simu <- mlbench.spirals(100,1,0.025)
plot(simu)

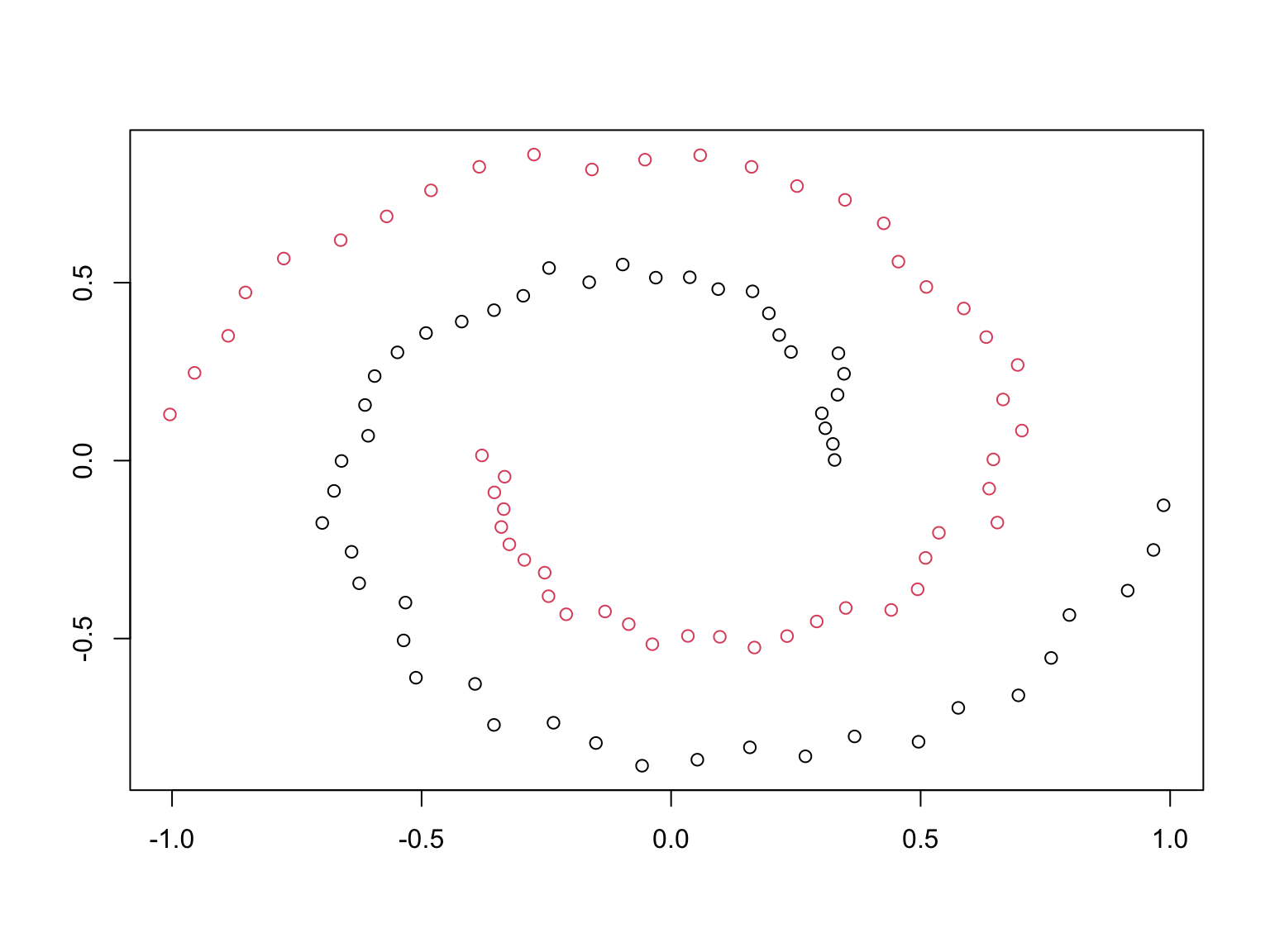
1. Pour commencer, appliquer l’algorithme de k-means directement sur ces données pour faire un clustering en deux groupes. Visualiser le clustering en représentant les points en couleur. Commenter le résultat.

2. Calculer les similarité gaussienne \(s_{ij}=\exp\{-\|x_i-x_j\|^2/(2\sigma^2)\}\) avec \(\sigma=1\).

   • Appliquer l’algorithme de spectral clustering normalisé sur ce graphe dense pour chercher deux classes. Analyser le spectre du laplacien normalisé et visualiser le clustering obtenu.

   • Tracer le nuage des nouveaux points sur lesquels \(k\)-means est appliquées (ce sont les lignes de la matrice T constituée des deux premiers vecteurs propres normalisés) et ajouter en couleur les classes initiales. Interpréter les résultats.

   • Appliquer l’algorithme de absolute spectral clustering avec deux classes. Analyser le spectre et visualiser le clustering obtenu.

3. Faites de même pour les graphes de similarité suivants:

   • On fixe \(\varepsilon=q_{0.75}\) le quantile à 75% des similarités \(\{s_{ij}\}_{i<j}\). Construire le graphe de \(\varepsilon\)-voisinage des points \(\{x_i\}\).
   • On fixe \(\varepsilon=q_{0.95}\) le quantile à \(95\%\) des similarités \(\{s_{ij}\}_{i<j}\). Construire le graphe de \(\varepsilon\)-voisinage des points \(\{x_i\}\).
   • On fixe \(p=2\lfloor \log(n)\rfloor\). Construire le graphe valué des \(p\) plus proches voisins mutuels des points \(\{x_i\}\).
   • On fixe \(p=2\). Construire le graphe valué des \(p\) plus proches voisins mutuels des points \(\{x_i\}\).
   • On fixe \(p=2\lfloor \log(n)\rfloor\). Construire le graphe valué des \(p\) plus proches voisins simple des points \(\{x_i\}\).
   • On fixe \(p=2\). Construire le graphe valué des \(p\) plus proches voisins simple des points \(\{x_i\}\).