2.2 Voisinage et degré

Une descripteur individuel de chaque noeud est son degré, qui repose sur son voisinage direct.

Definition 2.3 (Voisinage, degrés) Dans un graphe \(G=(V,E)\) non orienté les voisins de \(i\in V\) sont les noeuds \(j\in V\) tels que \(\{i,j\}\in E\). On note le voisinage de \(i\) par \[ \mathcal{V}(i)=\{j \in V ; \{i,j\}\in E\}. \] Le degré \(d_i\) d’un noeud \(i\) du graphe \(G\) est le nombre de voisins de \(i\) dans \(G\). C’est donc le cardinal \(|\mathcal{V}(i)|\) du voisinage de \(i\) dans \(G\).

Le degré moyen d’un graphe est défini par \[ \bar {d} = \frac 1 {|V|} \sum_{i \in V} d_i. \]

Si \(G\) est un graphe dirigé, on peut définir le degré sortant \(d_i^{\text{out}}\) et le degré entrant \(d_i^{\text{in}}\) du noeud \(i\) ainsi que les degrés moyens sortants par \[ \bar {d}^{\text{in}} = \frac 1 {|V|} \sum_{i\in V} d_i^{\text{in}} = \bar{d}^{\text{out}} = \frac 1{|V|}\sum_{i\in V} d_i^{\text{out}}. \]

Un hub est un noeud dont le degré est particulièrement grand.

Exercice.

  • Pour un graphe non dirigé, exprimer le degré \(d_i\) du noeud \(i\) en fonction de la matrice d’adjacence \(A\).
  • Même question pour les degrés entrant \(d_i^{\text{in}}\) et sortant \(d_i^{\text{out}}\) d’un graphe dirigé.
  • Montrer que les degrés moyens entrant et sortant sont égaux, à savoir \[\bar d^{\text{in}} =\bar d^{\text{out}}.\]
  • Pour un graphe non dirigé, simple, montrer que la somme de degrés de noeuds est égale à 2 fois la taille du graphe, à savoir \[|V|\bar d= 2|E|.\]

Distribution des degrés. Plus intéressant que le degré moyen est la distribution des degrés. Notons tout d’abord que le degré moyen \(\bar d\) n’est pas une variable très informative, car dans les réseaux observés, les degrés des noeuds varient beaucoup. La distribution des degrés contient plus d’information que le degré moyen.

Il faut cependant garder en tête que des graphes très différents peuvent avoir la même distribution des degrés des noeuds. Figure 2.2 montre deux graphes différents avec exactement la même suite de degrés. De la même façcon, si les variables aléatoires \(\bar{D}^{\text{in}}\) et \(\bar{D}^{\text{out}}\) sont toujours égales entre elles, la suite des degrés observés entrants \((D_i^{\text{in}})_{1\le i \le n}\) et sortants \((D_i^{\text{out}})_{1\le i \le n }\) peuvent être très différents.

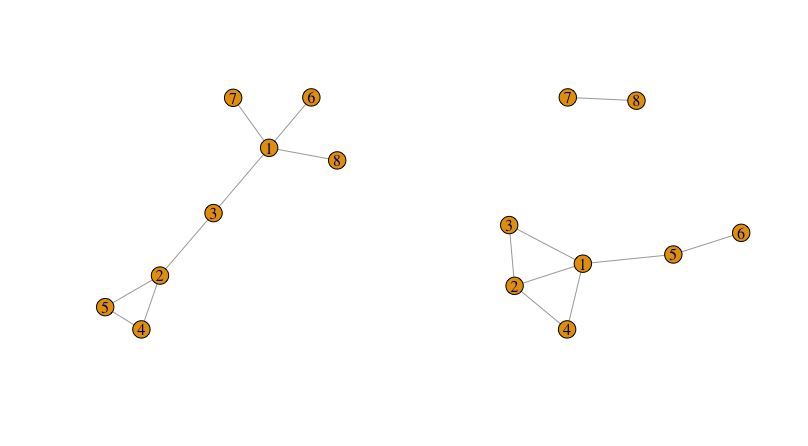
Exemple de deux graphes qui ont la même suite de degrés.

Figure 2.2: Exemple de deux graphes qui ont la même suite de degrés.