5.3 TP – Modularité

Illustrons d’abord l’algorithme de Girvan-Newman et la sélection du nombre de cluster basée sur la modularité sur un exemple.

On travaille avec la library igraph et on utilisera les fonctions suivantes:

library(igraph)
help("edge_betweenness")
help("cluster_edge_betweenness")

On construit le petit graphe suivant:

par(mar=c(0,0,0,0))
G1 <- make_full_graph(3)
G2 <- make_full_graph(3)
G3 <- make_full_graph(2)
G4 <- make_full_graph(3)
G5 <- make_full_graph(3)
G <- G1+G2+G3+G4+G5
G <- add.edges(G, c(6,7))
G <- add.edges(G, c(3,7))
G <- add.edges(G, c(8,9))
G <- add.edges(G, c(8,12))
plot(G)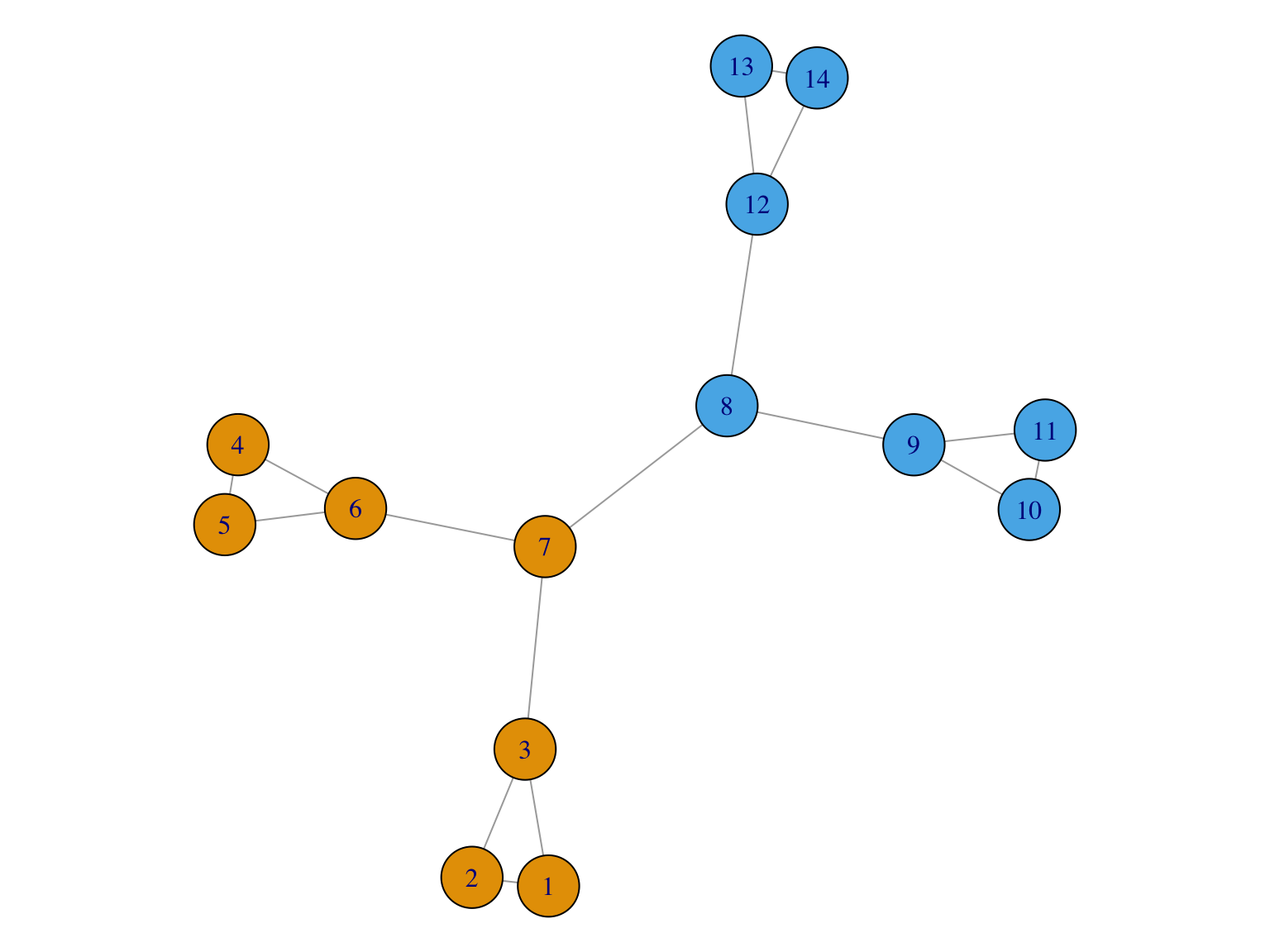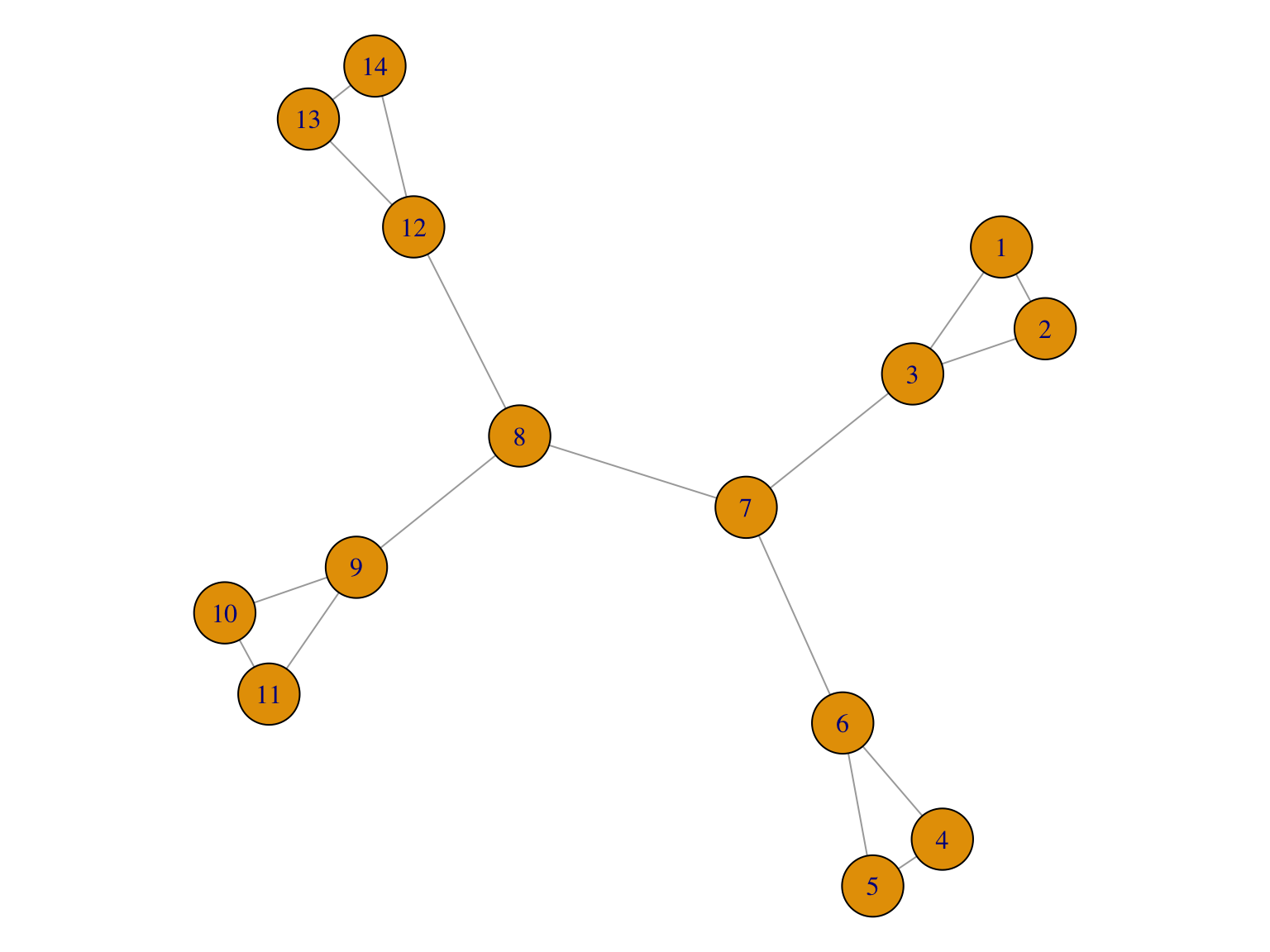

edge_betweenness(G)

##  [1]  1 12 12  1 12 12 49 12 12  1 12 12  1 33 33 33 33

E(G)

## + 17/17 edges from 58696dc:
##  [1]  1-- 2  1-- 3  2-- 3  4-- 5  4-- 6  5-- 6  7-- 8  9--10  9--11 10--11
## [11] 12--13 12--14 13--14  6-- 7  3-- 7  8-- 9  8--12

L’intermédiarité est la plus élevée pour la 7ème arête (avec une valeur de 49). C’est l’arête 7-8.

par(mar=c(0,0,0,0))
res <- cluster_edge_betweenness(G)
dendPlot(res)

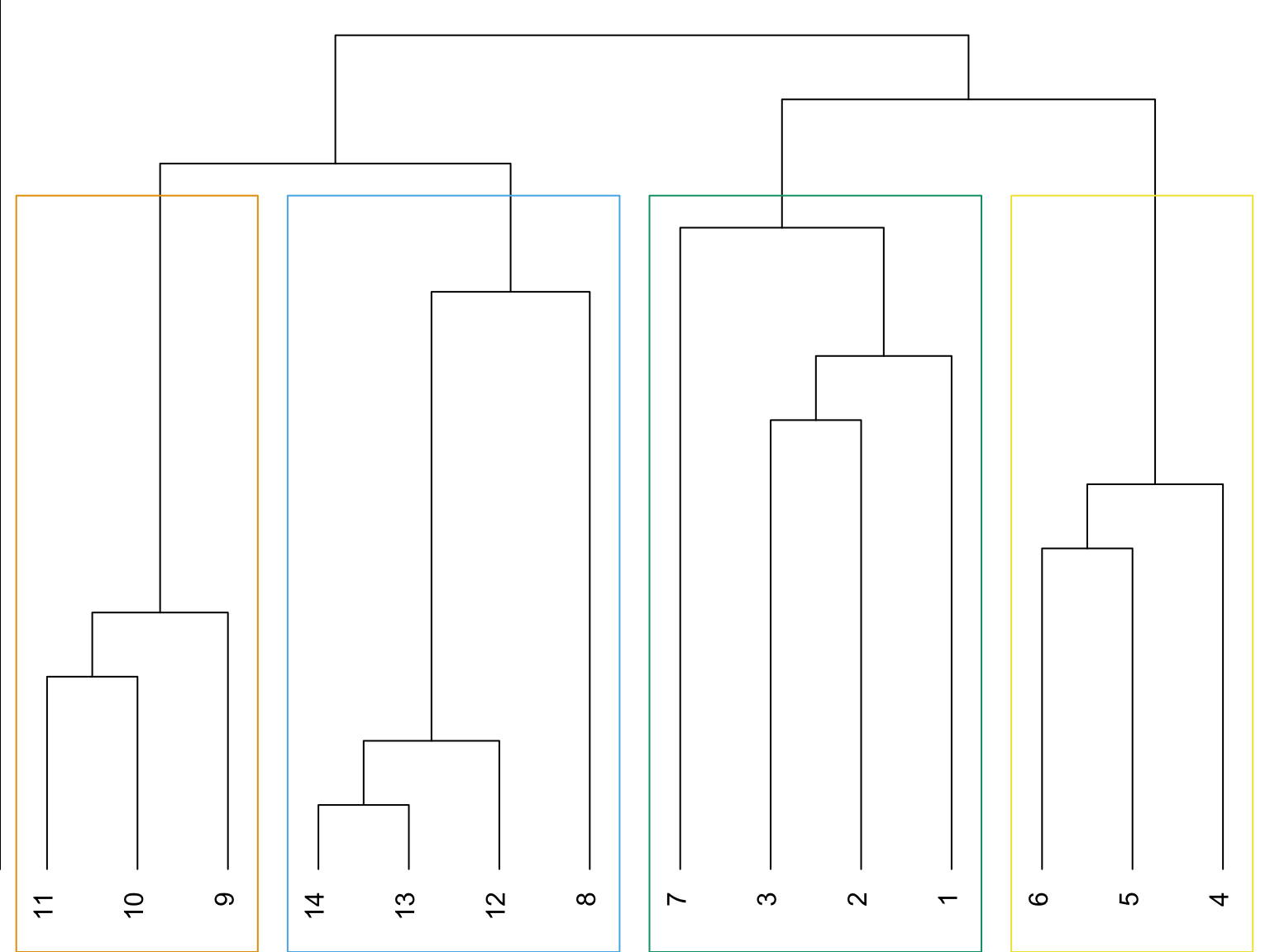
L’algorithme de Grivan-Newman a retiré l’arête 7-8: ce qui donne les clusters 1-7 et 8-14 Puis il a retiré l’arêtes 6-7: ce qui donne les clusters 4-5-6; 1-2-3-7 et 8-14…

Choix du nombre de clusters

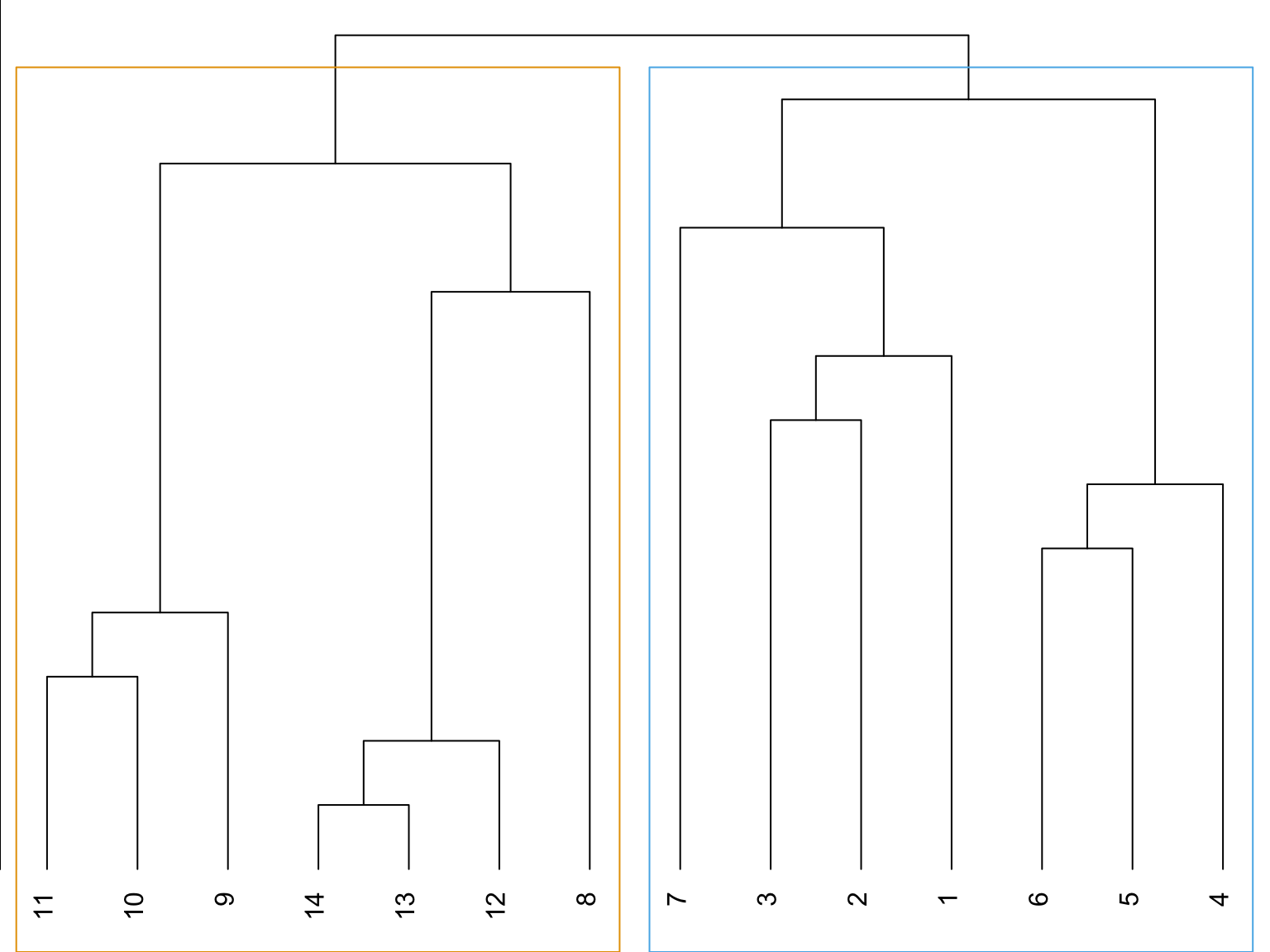
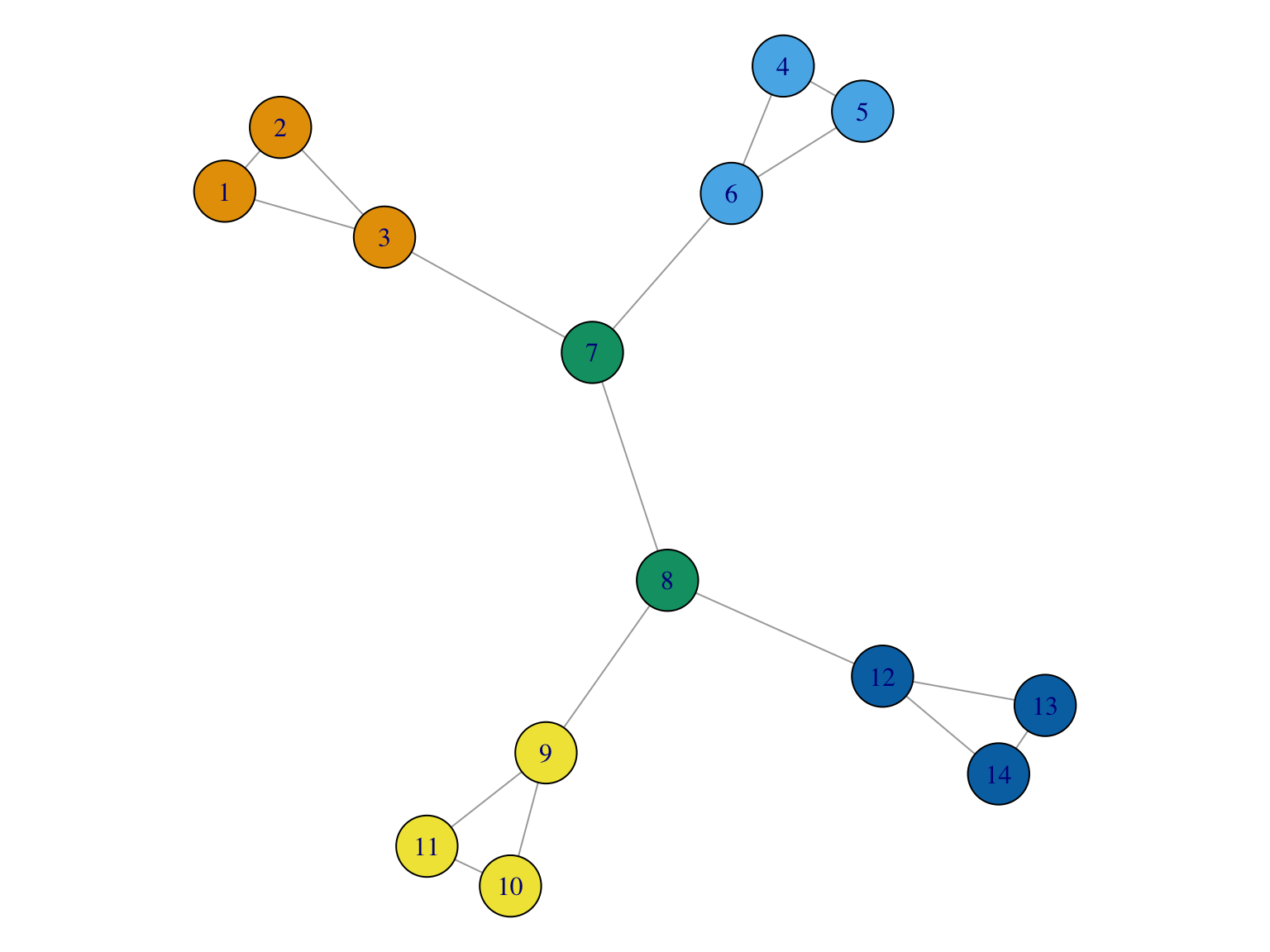
Le choix du nombre de clusters est basé sur la modularité. Ici on choisit 4 clusters:

par(mar=c(0,0,0,0))
dendPlot(res, mode="hclust")

plot(G, vertex.color=res$membership)

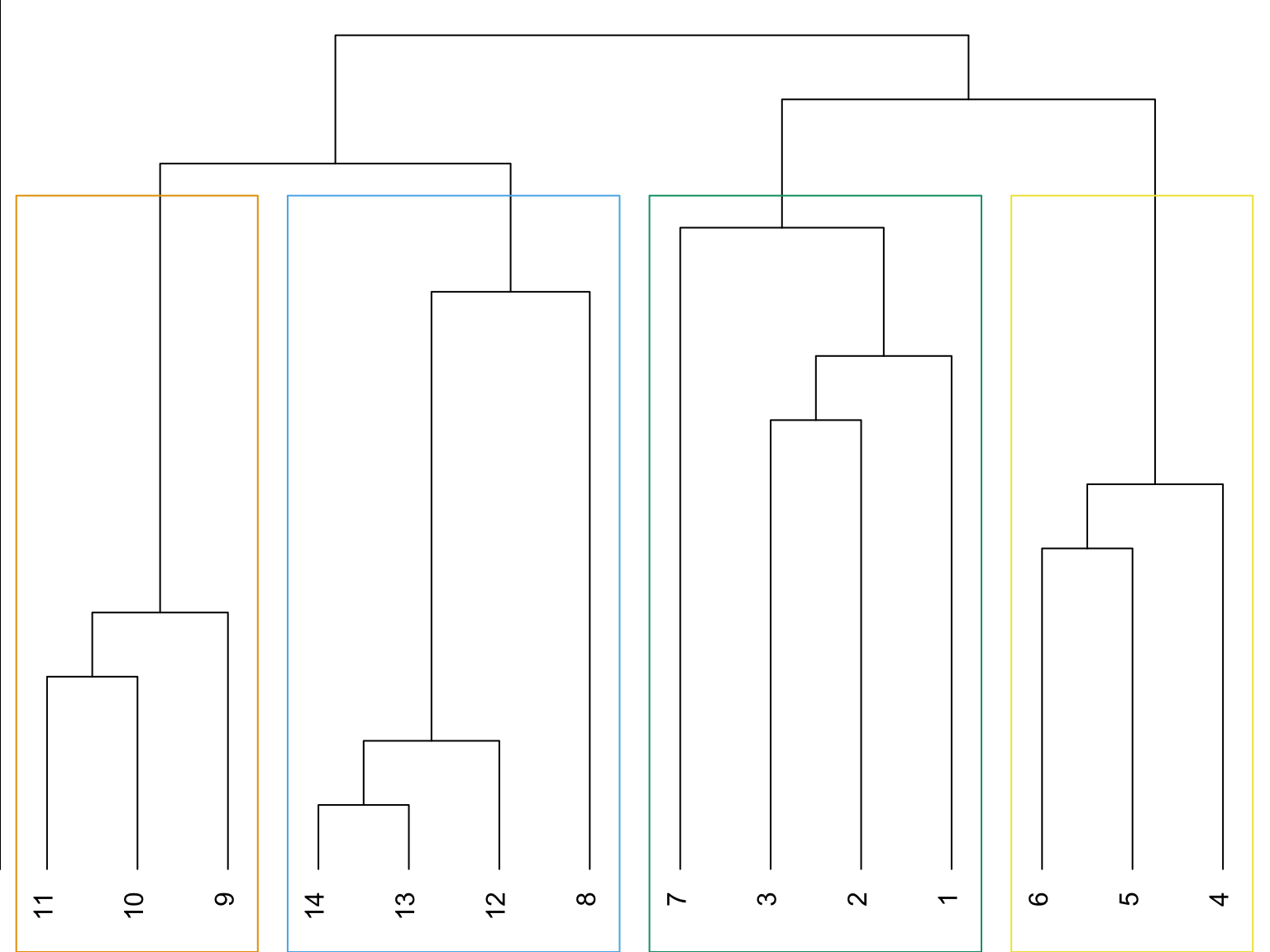
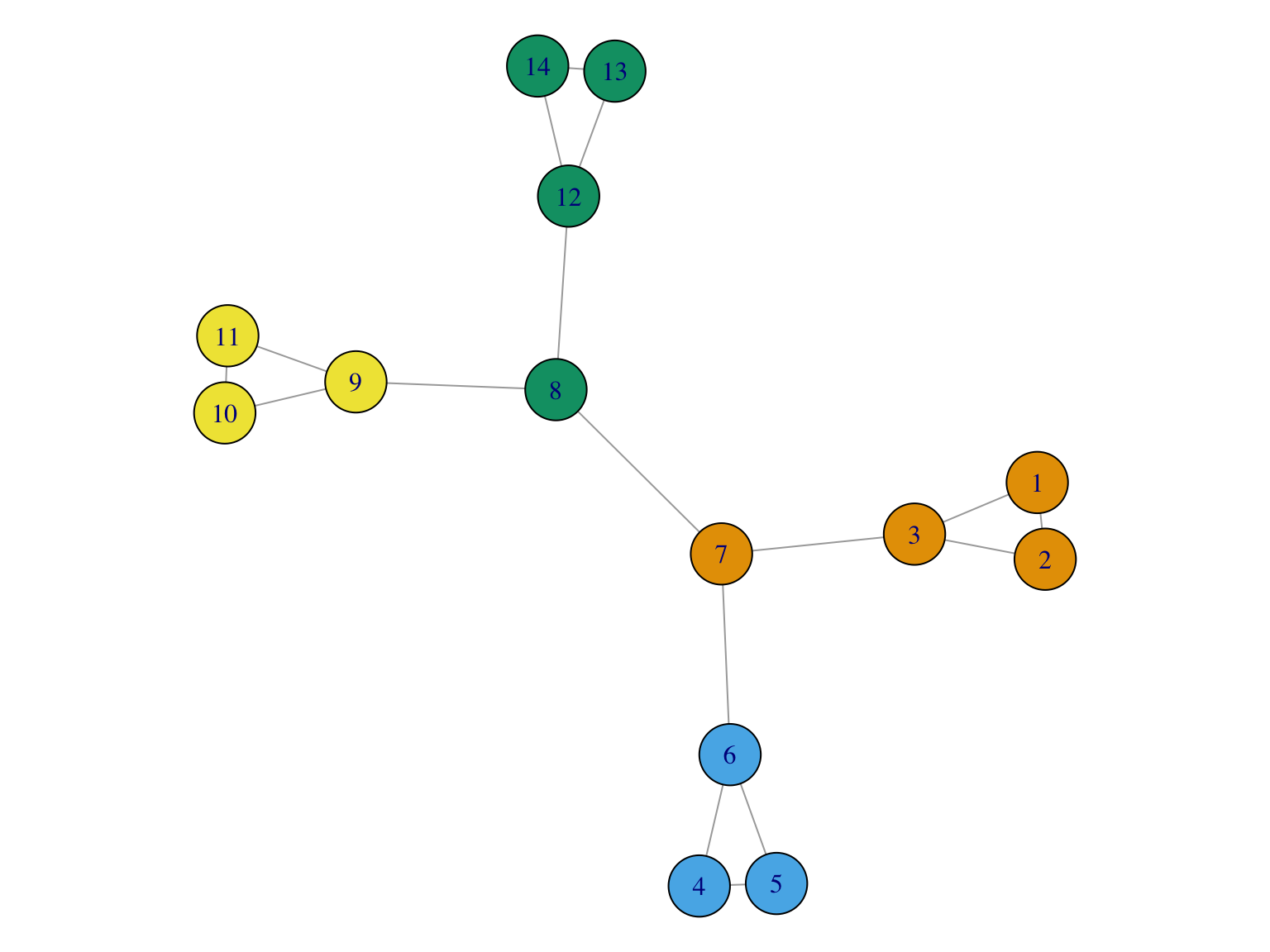
On peut choisir le nombre de clusters nous-même (coupure dans le dendogramme):

par(mar=c(0,0,0,0))
K <- 2
dendPlot(res, mode="hclust", rect=K)

grK <- cutat(res, no=K)
plot(G, vertex.color=grK)

Algorithme de Louvain

par(mar=c(0,0,0,0))
res <- cluster_louvain(G)
plot(G, vertex.color=res$membership)

Exercice

Maintenant, à vous sur le graphe karaté et sur le graphe friends.

Attention, la fonction cluster_edge_betweenness n’accepte pas les arêtes valuées, donc préciser weights=NULL si besoin. Importer le graphe friends en non dirigé.