1.3 Visualisation

En statistique, en général, la représentation graphique est un outil puissant d’exploration et d’analyse des données.

“L’excellence graphique est une présentation bien conçue des données d’intérêt […], [elle] vise à communiquer des idées complexes avec clarté, précision et efficacité; [elle] est ce qui donne au lecteur le plus grand nombre d’idées dans le temps le plus court, tout en utilisant le moins d’encre sur un minimum d’espace.” Tufte (2001).

La visualisation permet d’illustrer graphiquement les résultats, mais également de susciter des questionnements ou de valider des hypothèses.

Visualisation de graphes.

Concernant les graphes, la représentation graphique peut aider à comprendre la structure du graphe: y a-t-il des noeuds importants, des hubs ? des groupes de noeuds très connectés ?…

Il est clair que plus le graphe est grand, plus la lisibilité du graphique est difficile.

A priori on a le droit d’arranger les noeuds dans l’espace comme on veut. En revanche, le résultat visuel peut changer énormément d’une représentation à l’autre comme nous l’avons déjà observé dans la Figure 1.8. On constate que toute représentation est subjective et peut être trompeuse. La visualisation de graphe est un problème compliqué, dû en particulier à une grande complexité intrinsèque des données relationnelles ou d’interaction.

Bahoken, Beauguitte, and Lhomme (2013) proposent quelques règles générales pour la visualisation de graphes qui sont largement accepetées.

Trois principes de représentation de graphe

  • Les sommets les plus connectés sont placés au centre de la figure.
  • Les sommets les moins connectés sont placés en périphérie de la figure.
  • Il faut limiter, autant que possible, le chevauchement des liens.

Un graphe est dit planaire lorsque l’on peut le représenter dans le plan sans qu’aucune arête n’en croise une autre. A part pour la visualisation de graphe, cette propriété n’est pas très intéressante.

Dans la littérature on distingue différents différents positionnmenet des noeuds (Bahoken, Beauguitte, and Lhomme (2013)):

  • aléatoirement,
  • en cercle,
  • en étoile,
  • en arbre (pour des graphes acycliques),
  • selon différents algorithmes:
    • fondé sur l’analyse des données (p. ex. analyse spectrale de la matrice d’adjacence)
    • fondé sur la minimisation de l’énergie du système: système de forces entre des noeuds qui se repoussent et les arêtes assimilées à des ressorts qui tendent à rapprocher les noeuds voisins. Les résultats sont esthétiques, mais le temps de calcul peut être long, car l’algorithme est itératif (Fruchterman and Reingold (1991), Kamada and Kawai (1989)).

La Figure 1.9 montre différentes représentations du réseau trophique de le Figure 1.5. Sous R, dans le package igraph l’option layoutde la fonction plot permet de définir le type de représentation du graphe. Sous python, le package NetworkX propose différentes approches de visualitions.

plot(foodweb, layout=layout.fruchterman.reingold, edge.arrow.size=.5, edge.color='black')
plot(foodweb, layout=layout.lgl, edge.arrow.size=.5, edge.color='black')
plot(foodweb, layout=layout_in_circle, edge.arrow.size=.5, edge.color='black')
plot(foodweb, layout=layout_as_tree, edge.arrow.size=.5, edge.color='black')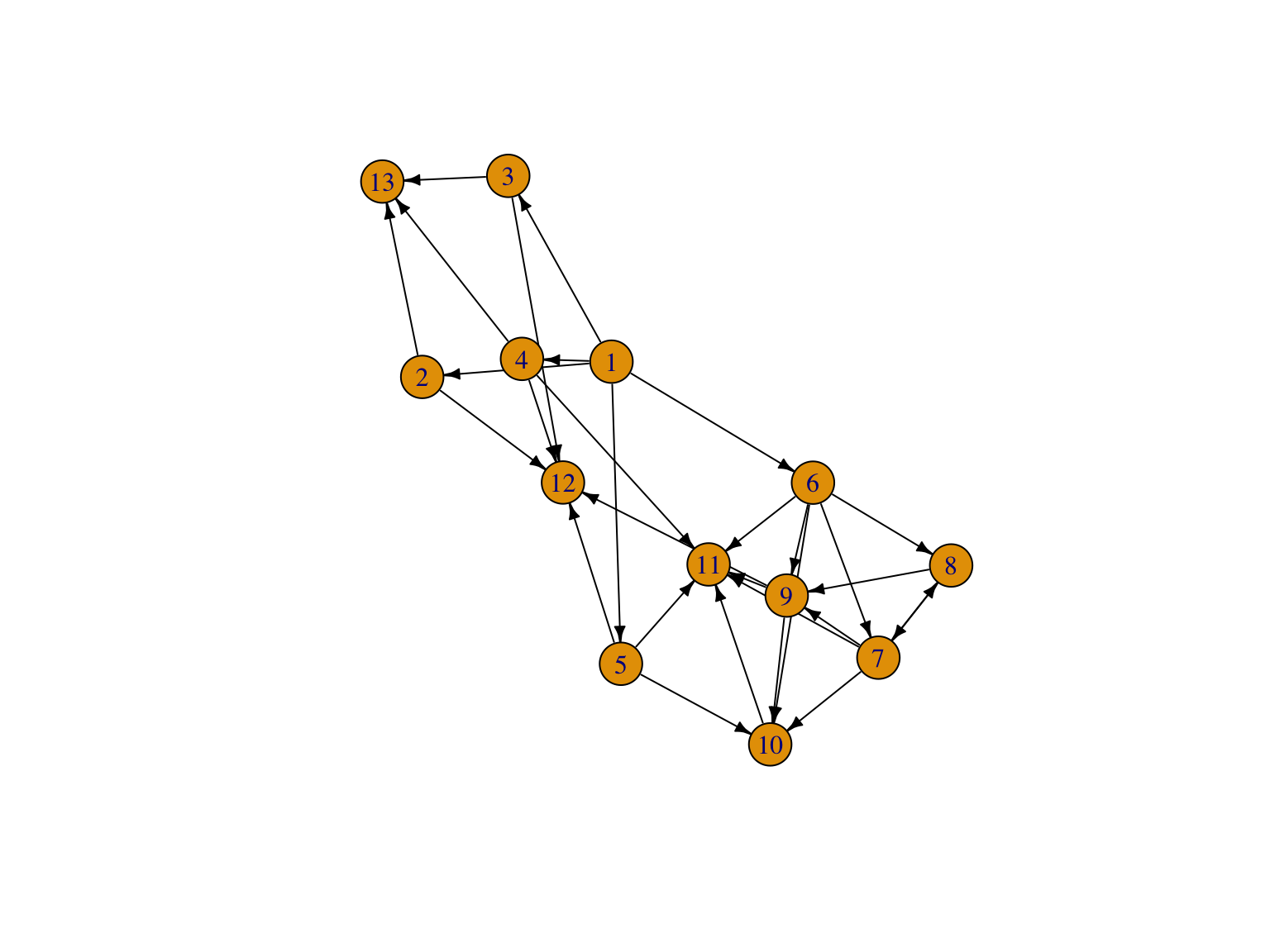
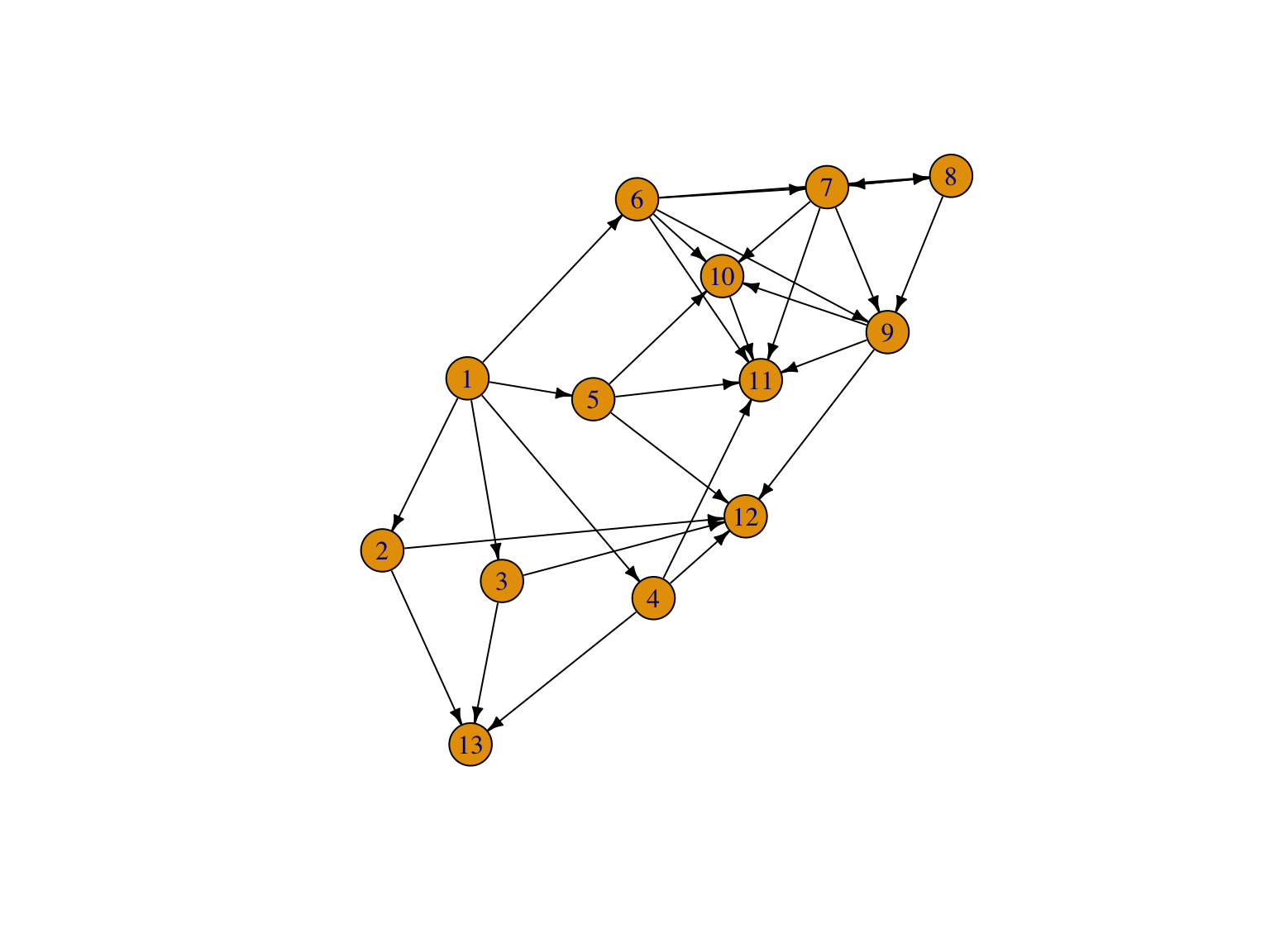
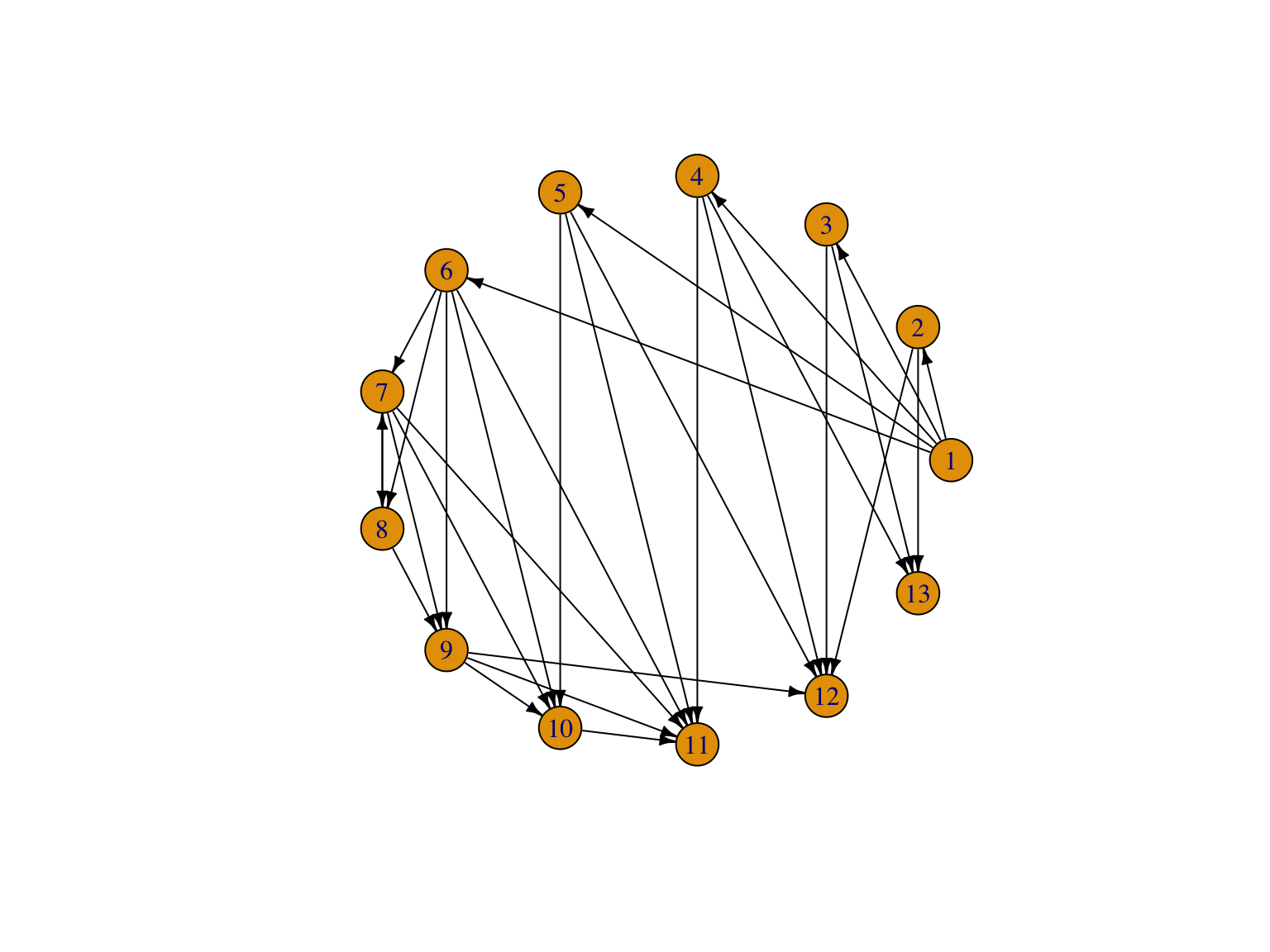
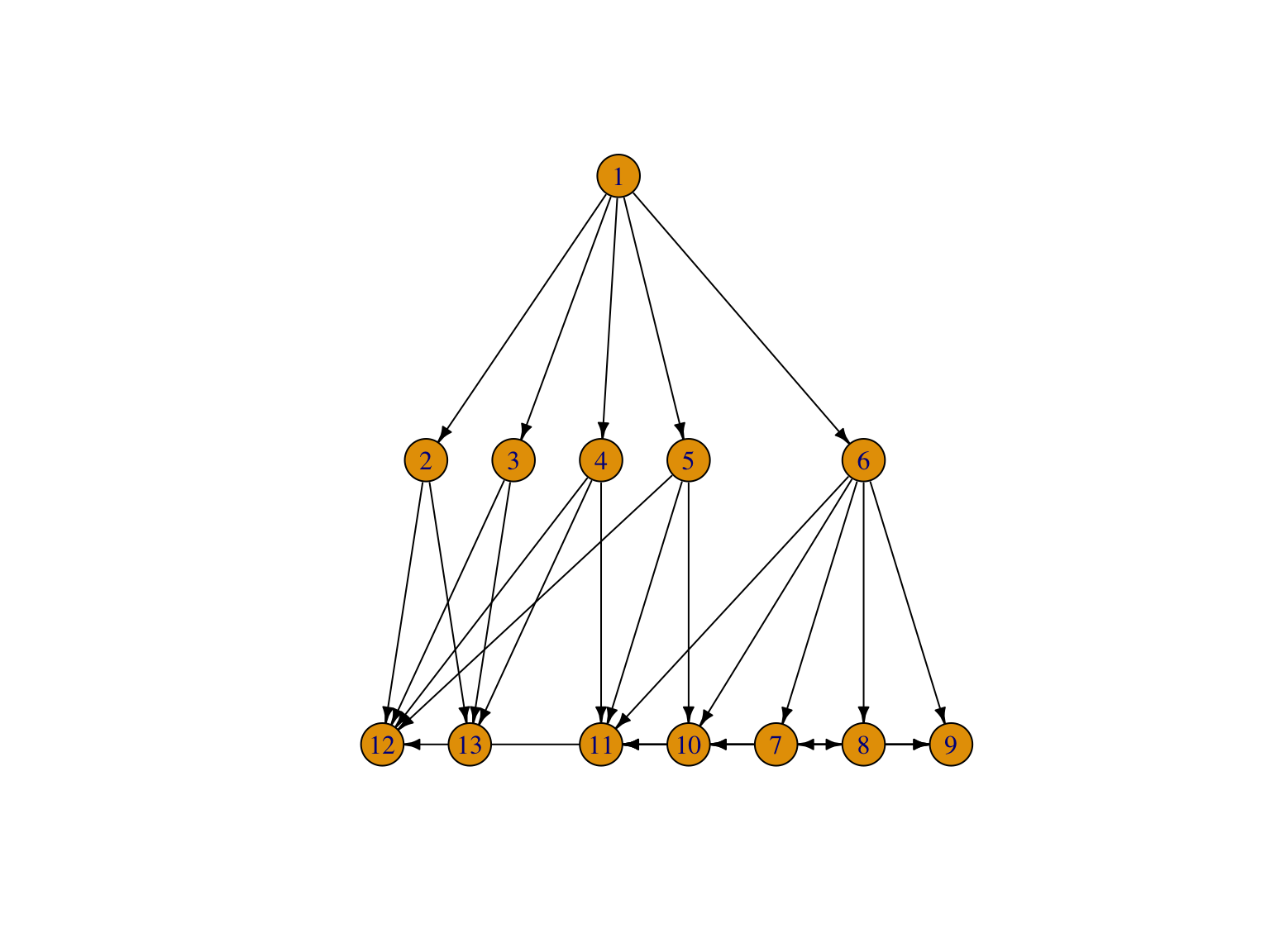
Différentes visualisations du graphe trophique de le Figure 1.5. La dernière représentation est partielle et produit un warning.Différentes visualisations du graphe trophique de le Figure 1.5. La dernière représentation est partielle et produit un warning.Différentes visualisations du graphe trophique de le Figure 1.5. La dernière représentation est partielle et produit un warning.Différentes visualisations du graphe trophique de le Figure 1.5. La dernière représentation est partielle et produit un warning.

Figure 1.9: Différentes visualisations du graphe trophique de le Figure 1.5. La dernière représentation est partielle et produit un warning.

Représentations visuelles avancées.

Souvent, les données ne sont pas uniquement de type relationnelles, et on peut disposer de covariables sur les individus qui composent le graphe. Ces covariables peuvent être incluses dans la représentation, par exemple en jouant sur la couleur (covariable catégorielle) ou la taille (covariable quantitative) des noeuds.

References

Bahoken, Françoise, Laurent Beauguitte, and Serge Lhomme. 2013. “La visualisation des réseaux. Principes, enjeux et perspectives.” https://halshs.archives-ouvertes.fr/halshs-00839905.

Fruchterman, Thomas M. J., and Edward M. Reingold. 1991. “Graph Drawing by Force-Directed Placement.” Software: Practice and Experience 21 (11): 1129–64.

Kamada, T., and S. Kawai. 1989. “An Algorithm for Drawing General Undirected Graphs.” Information Processing Letters 31 (1): 7–15.

Tufte, Edward R. 2001. The Visual Display of Quantitative Information. Cheshire, CT: Graphics Press.