Chapitre 4 Spectral clustering

Ce chapitre repose en grande partie sur l’article de Luxburg (2007).

L’analyse de grands graphes passe souvent par un résumé de l’information, par exemple à travers un partitionnement ou clustering, des noeuds du graphe: on va alors chercher à grouper les individus en classes homogènes, i.e. les individus dans la même classe se comportent de façon similaire au sein du graphe.

Nous verrons plusieurs façons de faire du partitionnement des noeuds d’un graphe dans ce cours. Ce chapitre s’intéresse prinicipalement au clustering spectral, qui est une technique de partitionnement qui détecte des noeuds très connectés entre eux. En ce sens, le clustering spectral est adapté à la recherche de communautés dans des graphes. Une communauté est un groupe de noeuds qui forme une quasi-clique, i.e. qui sont très connectés entre eux.

L’heuristique du spectral clustering est simple: si le graphe est composé de communautés, alors il existe une permutation des lignes et des colonnes de la matrice d’adjacence pour laquelle cette matrice est presque diagonale par blocs. Il suffit donc de diagonaliser la matrice d’adjacence (ou une version normalisée) pour trouver cette permutation.

Le spectral clustering est une technique de partitionnement utilisée de façon plus large que dans la simple analyse de graphes: on va voir qu’il peut-être utilisé pour le clustering des données d’un tableau de données classique, par exemple comme une alternative à l’algorithme de \(k\)-means, à partir du graphe de similarité des données. Le spectral clustering est une méthode qui n’est pas fondée sur un modèle probabiliste. Elle a l’avantage de fonctionner sur de très grands graphes.

Au chapitre suivant nous verrons d’autres approches pour la détection de communautés.

Dans tout ce chapitre, on ne considère que des graphes non dirigés.

Types de groupes de noeuds

Pour partitionner les noeuds d’un graphe, il faut bien préciser le type de groupe que l’on recherche.

La Figure 4.1 montre deux partionnements différents des noeuds d’un même graphe. A gauche, les deux groupes sont formés de noeuds fortement connectés entre eux et peu connectés aux noeuds de l’autre groupe. Ce sont des communautés. A droite, un groupe rassemble tous les noeuds périphériques, l’autre les noeuds à fort degrés, très connectés aux noeuds du premier groupe. Ici, la définition de groupe repose sur le rôle que jouent les noeuds dans le graphe.

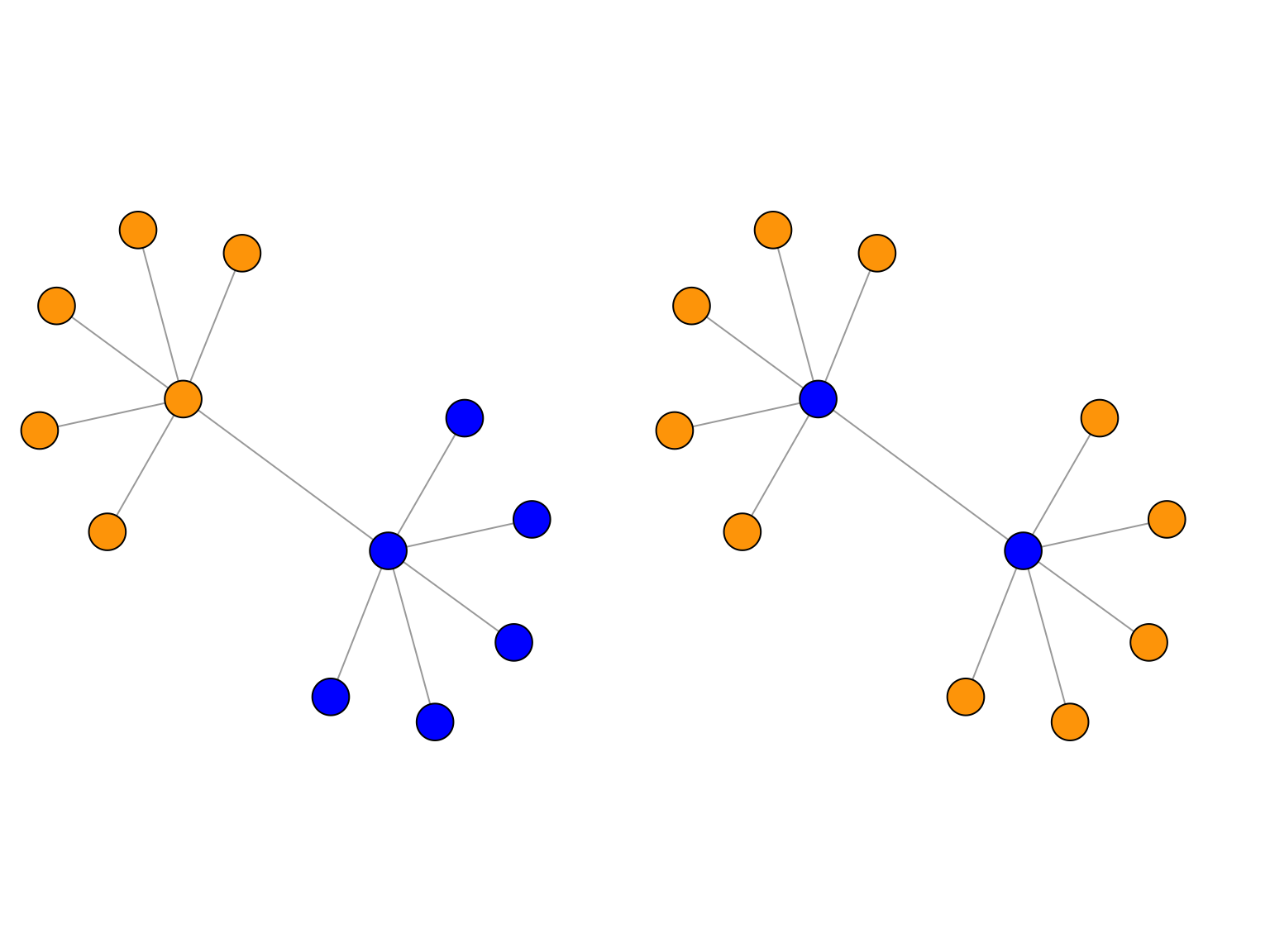
Figure 4.1: Deux partionnements différents pour les noeuds d’un même graphe

Les deux partitionnement dans la Figure 4.1 sont valides. Il faut choisir le type de groupes à rechercher en fonction du contexte et de l’objectif de l’analyse. Dans ce chapitre nous nous concentrons sur la détection de communautés. Ultérieurément, nous verrons des méthodes adaptées à une notion de groupe bien plus flexible.

References

Luxburg, Ulrike von. 2007. “A Tutorial on Spectral Clustering.” Statistics and Computing 17 (4): 395–416. http://dx.doi.org/10.1007/s11222-007-9033-z.