8.2 Vraisemblance

Dans la suite, on note le paramètre global du modèle \(\boldsymbol \theta=(\boldsymbol \pi,\boldsymbol \gamma) = ((\pi_1,\dots, \pi_Q) ; (\gamma_{q \ell})_{q, \ell})\).

Vraisemblance des données complètes. Comme dans tous les modèles à variables latentes, il est facile d’écrire la fonction de vraisemblance des données complètes. Pour un SBM non dirigé de paramètre \(\boldsymbol \theta\) avec des observations \(\mathbf A=(A_{i,j})_{i<j}\) et variables latentes \(\mathbf Z=(Z_1,\dots,Z_n)\) on obtient pour la vraisemblance des données complètes \((\mathbf A,\mathbf Z)\) \[\begin{align*} \mathbb P_{\boldsymbol \theta}(\mathbf A, \mathbf Z) =& \left(\prod_{i=1}^n \pi_{Z_{i}} \right) \times \left(\prod_{i<j} F(A_{i,j} ; \gamma_{Z_i, Z_j}) \right) \\ =& \left(\prod_{q=1}^Q \prod_{i=1}^n\pi_q^{Z_{i,q}} \right) \times \left(\prod_{1\le q,\ell \le Q} \prod_{i,j} F(A_{i,j} ; \gamma_{q,\ell})^{Z_{i,q}, Z_{j,\ell}} \right), \end{align*}\] et la log-vraisemblance des données complètes s’écrit simplement \[\begin{equation} \tag{8.1} \log \mathbb P_{\boldsymbol \theta}(\mathbf A, \mathbf Z) = \sum_{q=1} ^Q \sum_{i=1}^nZ_{i,q} \log \pi_q + \sum_{1\le q,\ell \le Q} \sum_{i<j} {Z_{i,q} Z_{j,\ell}} \log F(A_{i,j} ; \gamma_{q,\ell}) . \end{equation}\] On peut vérifier que l’estimateur de maximum de vraisemblance de \(\theta\) est explicite si on dispose des données complètes \((\mathbf A,\mathbf Z)\).

Vraisemblance des données incomplètes. La fonction de la vraisemblance des données complètes est obtenue par la somme de la vraisemblance complète sur toutes les valeurs possibles des variables latentes \(\mathbf Z=(Z_1,\dots,Z_n)\), à savoir \[\begin{align*} \mathcal L(\theta) =& \mathbb P_{\boldsymbol \theta}(\mathbf A) \\ =& \sum_{z_1=1}^Q \dots \sum_{z_n=1} ^Q \mathbb P_{\boldsymbol \theta}(\mathbf A, Z_1=z_1,\dots, Z_n =z_n) \\ =& \sum_{z_1=1}^Q \dots \sum_{z_n=1}^Q \left(\prod_{q=1}^Q \pi_q^{\sum_i Z_{i,q}} \right) \times \left(\prod_{1\le q,\ell \le Q} F(A_{i,j} ; \gamma_{q,\ell})^{\sum_{i<j} Z_{i,q} Z_{j,\ell}} \right). \end{align*}\] Notons que cette somme a \(Q^n\) termes, et par ce fait, elle est incalculable en pratique.

Pour la log-vraisemblance des données incomplètes on obtient \[\begin{align*} \ell(\theta) &:= \log(\mathcal L(\theta))\\ &=\log \left(\sum_{z_1=1}^Q \dots \sum_{z_n=1}^Q \left(\prod_{q=1}^Q \pi_q^{\sum_i Z_{i,q}} \right) \times \left(\prod_{1\le q,\ell \le Q} F(A_{i,j} ; \gamma_{q,\ell})^{\sum_{i<j} Z_{i,q} Z_{j,\ell}} \right)\right). \end{align*}\] Il est clair que l’estimateur du maximum de vraisemblance n’est pas explicite.

Lois conditionnelles et graphe moral. Pour mettre en oeuvre l’algoirthme EM, on aura besoin de la loi aposteriori des variables latentes \(\mathbf Z\) sachant les observations \(\mathbf A\). La Figure 8.4 montre le modèle graphique dirigé du SBM ainsi que son graphe moral.

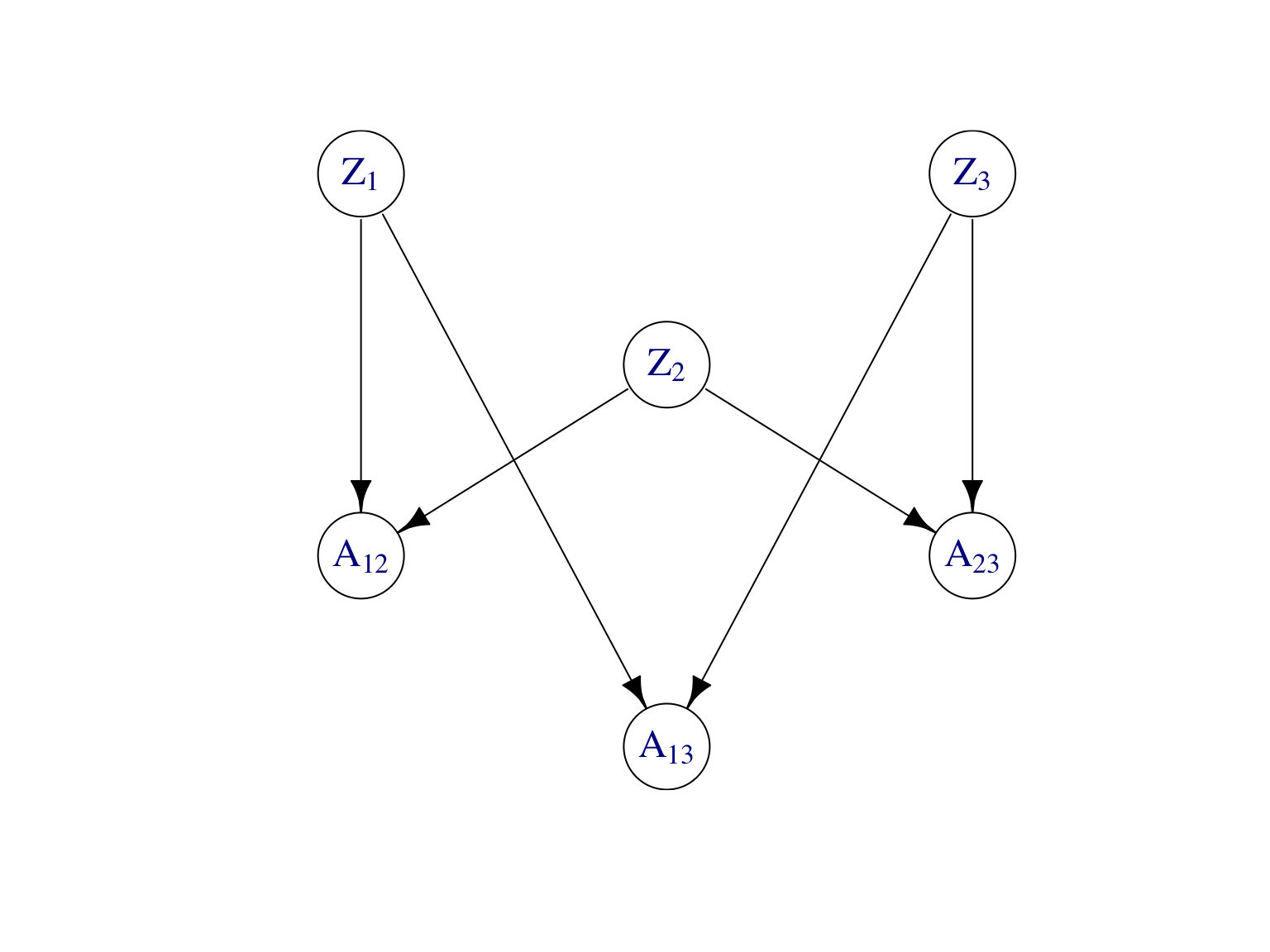
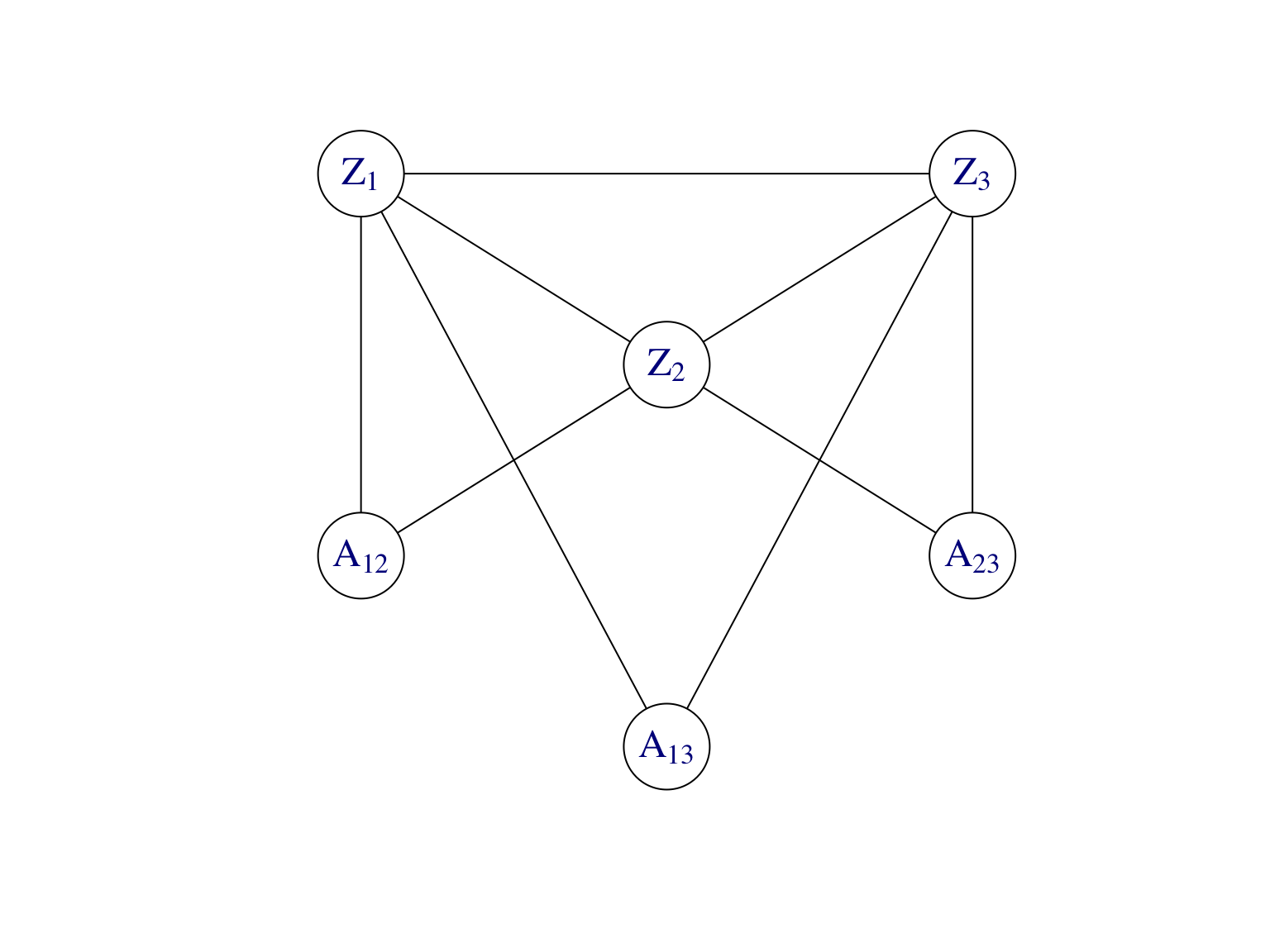
Figure 8.4: Modèle graphique dirigé et son graphe moral d’un SBM à \(n=3\) noeuds.

Dans le graphe moral les \((Z_i)_i\) forment une clique. Par conséquent, la loi conditionnelle de \(\mathbf Z\) sachant les observations \(\mathbf A\) ne se factorise pas, i.e. les variables latentes \(Z_i\) ne sont pas indépendantes conditionnellement à \(\mathbf A\). On a \[\begin{align} \tag{8.2} \mathbb P(\mathbf Z|\mathbf A)\neq \prod_{i=1}^n\mathbb P(Z_i|\mathbf A). \end{align}\] Au fait, dans un SBM, conditionnellement aux observations, toutes les variables latentes \(Z_i\) sont dépendantes. Heuristiquement, pour déterminer p.ex. la probabilité conditionnelle que \(Z_1\) appartient au groupe \(1\), il faut savoir pour tout \(j>1\) si \(A_{1,j}\) est l’interaction avec un noeud du groupe 1, 2, 3 etc. et donc il faut connaitre les valeurs de toutes les variables latentes \(Z_2,\dots,Z_n\).