8.6 TP – SBM

Exercice 1. Simulation d’un SBM

On note \(n\) le nombre de noeuds, \(\boldsymbol\pi=(\pi_1,\dots,\pi_Q)\) les proportions des \(Q\) groupes latents, et \(\boldsymbol \gamma\) la matrice de connectivité (de taille \(Q\times Q\)) d’un modèle à blocs stochastiques. Ici, on ne considère que les graphes binaires et non dirigés.

  1. Ecrire une fonction rsbm qui
  • prend en argument les paramètres d’un SBM,
  • simule un graphe de ce modèle et
  • renvoie sa matrice d’adjacence ainsi que les variables latentes.

  1. Générer un SBM avec les paramètres suivants: \(n=15\), \(\pi=(1/2,1/2)\) et \[\boldsymbol \gamma=\left(\begin{array}{ll}0.8&0.1\\0.1&0.6\end{array}\right),\] et visualiser le graphe simulé.

  2. Choisir les paramètres d’un modèle plus complexes (avec plus de groupes, modèle disassortatif etc.). Simuler un graphe, visualiser-le et visualiser aussi le métagraphe du modèle associé à la matrice de connectivité \(\boldsymbol \gamma\).

Remarque : dans igraph, la fonction sample_sbm permet aussi de simuler des SBM, mais c’est un très bon exercice d’écrire sa propre fonction de simulation !

Package sbm

Le package sbm regroupe les fonctions de plusieurs packages qui traitent des variantes du modèle à blocs stochastiques. L’idée est d’offrir à l’utilisateur une interface unique via un seul package avec des noms d’objet ou de fonction unifiés. Le package sbm est en cours de développement. A terme il devrait inclure au moins 5 variantes ou extensions de SBM. Pour l’analyse de SBM binaires ou valués, le package sbm utilise les fonctions du package blockmodels dans lequel l’algorithme VEM que nous avons vu en cours est implémenté de manière efficace.

Prenons un graphe simulé de l’exercice précédent :

pi <- c(.5, .5) # group proportions  
gamma <- matrix(c(0.8, 0.1,
                  0.1, 0.6), nrow=2) # connectivity matrix 
n <- 15 # number of nodes
SBMcomm <- rsbm(n, pi, gamma)

On charge le package sbm :

library(sbm)

La fonction plotMyMatrix affiche la matrice d’adjacence :

plotMyMatrix(SBMcomm$adj)

On voit bien que notre matrice d’adjacence est symétrique.

La fonction estimateSimpleSBM applique l’algorithme VEM à une matrice d’adjacence pour estimer les paramètres d’un SBM comme défini dans le cours. La fonction recherche automatiquement le bon nombre de groupes \(Q\) selon le critère ICL. Le deuxième argument de la fonction spécifie la distribution des arêtes. Pour le SBM binaire on choisit "bernoulli" (valeur par défaut). Si le SBM est valué, on a le choix entre "poisson" et "gaussian". Les valeurs de l’argument estimOptions que l’on choisit ci-dessous font taire la fonction pour le moment (on revient là-dessus plus tard). (Pour info, estimateSimpleSBM appelle la fonction BM_bernoulli du package blockmodels).

mySimpleSBM <- estimateSimpleSBM(SBMcomm$adj, 
                                 "bernoulli", 
                                 estimOptions = list(verbosity = 0, plot = FALSE))
mySimpleSBM
## Fit of a Simple Stochastic Block Model -- bernoulli variant
## =====================================================================
## Dimension = ( 15 15 ) - ( 2 ) blocks and no covariate(s).
## =====================================================================
## * Useful fields 
##   $dimension, $modelName, $nbNodes, $nbBlocks, $nbCovariates, $nbDyads
##   $blockProp, $connectParam, $covarParam, $covarList, $covarEffect, $dimLabels 
##   $probMemberships, $memberships, $loglik, $ICL, $storedModels, $setModel 
## * S3 methods 
##   plot, print, coef, predict, fitted

La sortie est un objet avec de nombreuses informations.

# nb de noeuds dans le graphe (on sait déjà)
mySimpleSBM$nbNodes
## [1] 15
# nb de groupes Q choisi par ICL (ici la méthode a choisi le bon nombre)
mySimpleSBM$nbBlocks
## [1] 2

Ici la fonction plot avec l’option type = "data" affiche la matrice d’adjacence où les noeuds sont réordonnés en fonction de leur appartenance de groupe dans le SBM :

plot(mySimpleSBM, type = "data")

On distingue bien les deux groupes et les différents profils de connexion des noeuds.

Avec l’option type = "expected", on peut afficher la matrice des probabilités de connexion pour chaque paire de noeuds, ce qui correspond à l’espérance de la matrice d’adjacence :

plot(mySimpleSBM, type = "expected")

C’est forcément une matrice par blocs.

Maintenant, intéressons-nous aux paramètres estimés par l’algorithme VEM. On les obtient avec la fonction coef.

# les proportions de groupe :
coef(mySimpleSBM, 'block')
## [1] 0.6000407 0.3999593
# qui devrait être proche de pi, mais comme il n'y a que 15 noeuds on est un peu loin :
pi
## [1] 0.5 0.5
# les paramètres de connectivité
coef(mySimpleSBM, 'connectivity')
## $mean
##            [,1]       [,2]
## [1,] 0.54889511 0.06256332
## [2,] 0.06256332 0.71952487
# que l'on espère proche du vrai gamma :
gamma
##      [,1] [,2]
## [1,]  0.8  0.1
## [2,]  0.1  0.6

Dans cet exemple, nous voyons bien que les groupes ont été permutés : c’est le groupe 2 qui a l’intra-connectivité la plus élevée, alors que dans la matrice gamma de départ c’est le groupe 1. Ce problème de label-switching est le même que l’on connait des modèles de mélange. Ces modèles à variables latentes ne sont identifiables qu’à permutation près des groupes. Pour l’estimation par VEM, cela n’est pas vraiment gênant. En revanche, quand on compare les paramètres de deux modèles (comme ci-dessus les paramètres estimés au vraies valeurs des paramètres) il faut en tenir compter.

Revenons à la sélection de modèle via le critère ICL. D’abord, nous relançons l’algorithme VEM, en permettant à la fonction de nous parler :

mySimpleSBM <- estimateSimpleSBM(SBMcomm$adj, 
                                 "bernoulli")
## -> Estimation for 1 groups
## 

## -> Computation of eigen decomposition used for initalizations
## 
## -> Pass 1
##     -> With ascending number of groups
##         -> For 2 groups
## 

##         -> For 3 groups
## 

##         -> For 4 groups
## 

##     -> With descending number of groups
##         -> For 3 groups
## 

##         -> For 2 groups
## 

## -> Pass 2
##     -> With ascending number of groups
##         -> For 2 groups
##         -> For 3 groups
##         -> For 4 groups
##     -> With descending number of groups
##         -> For 3 groups
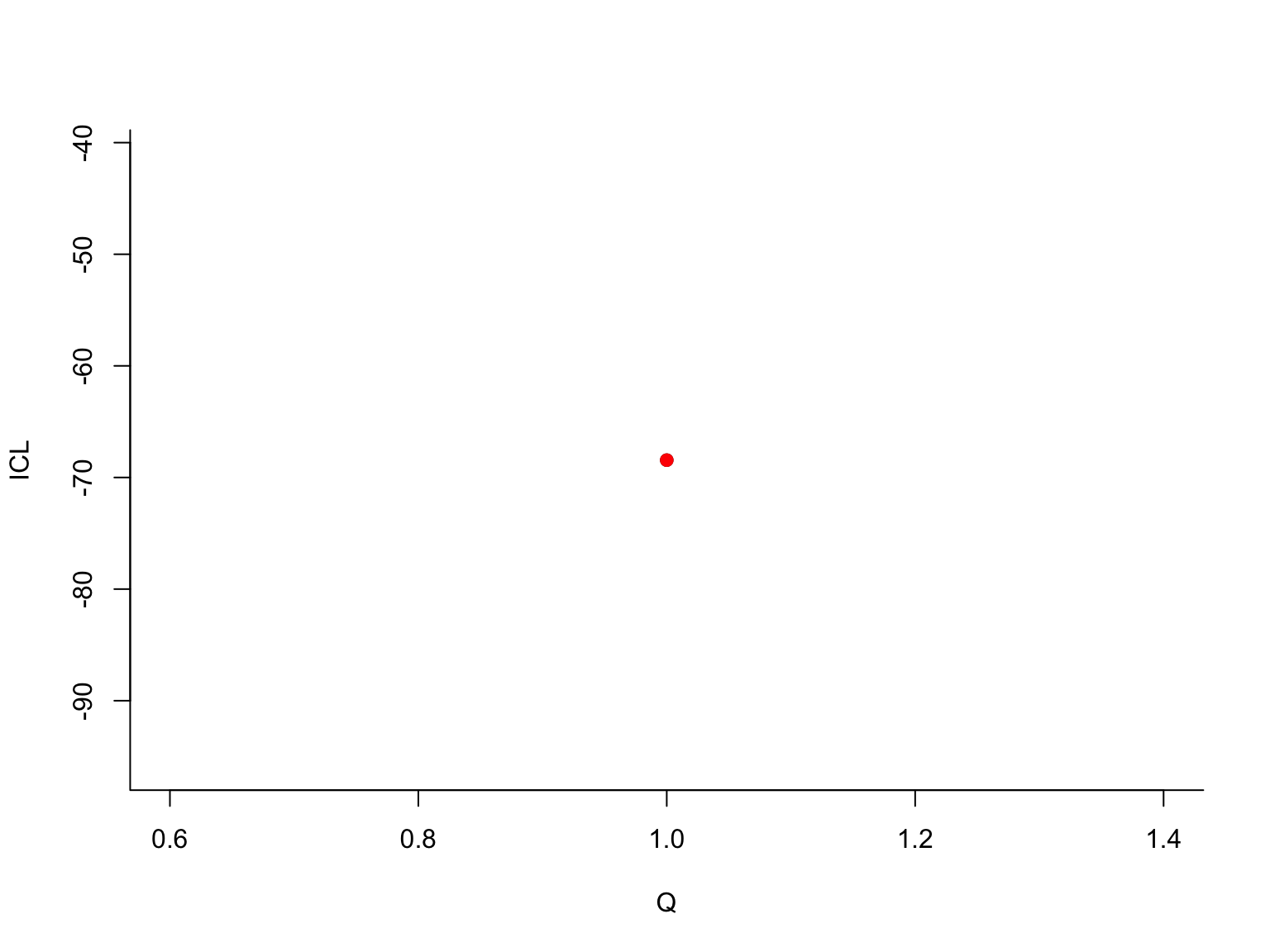
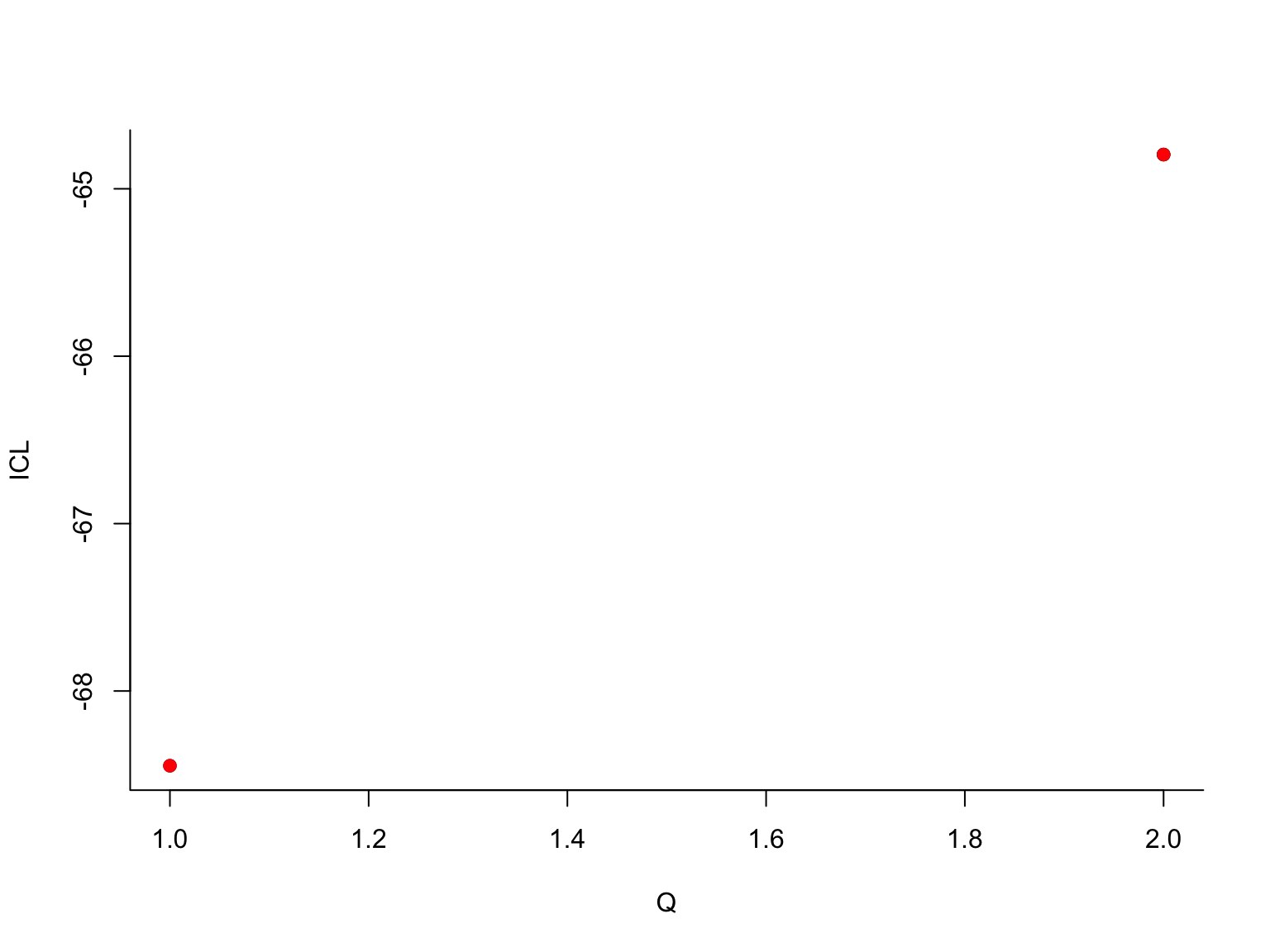
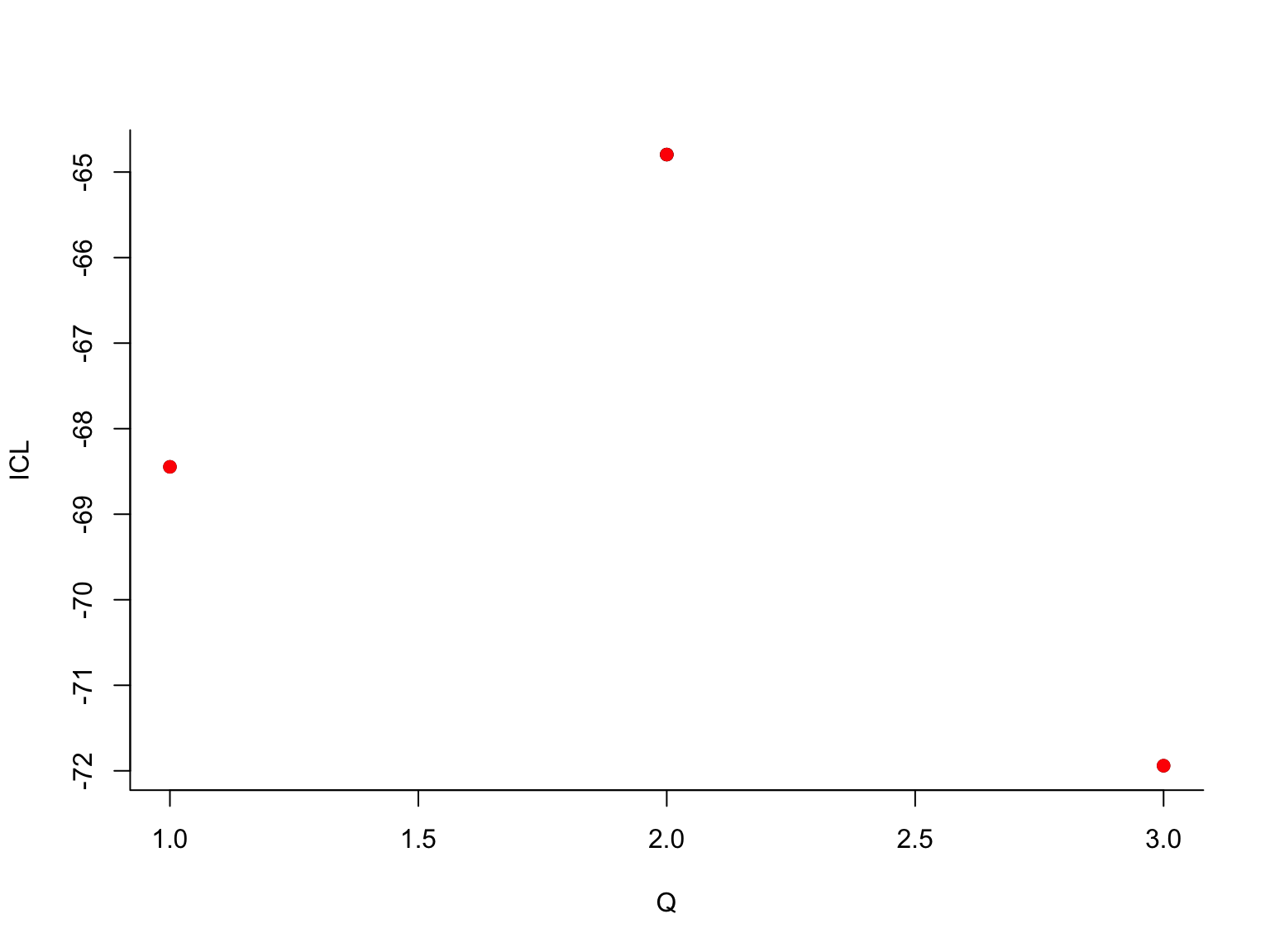
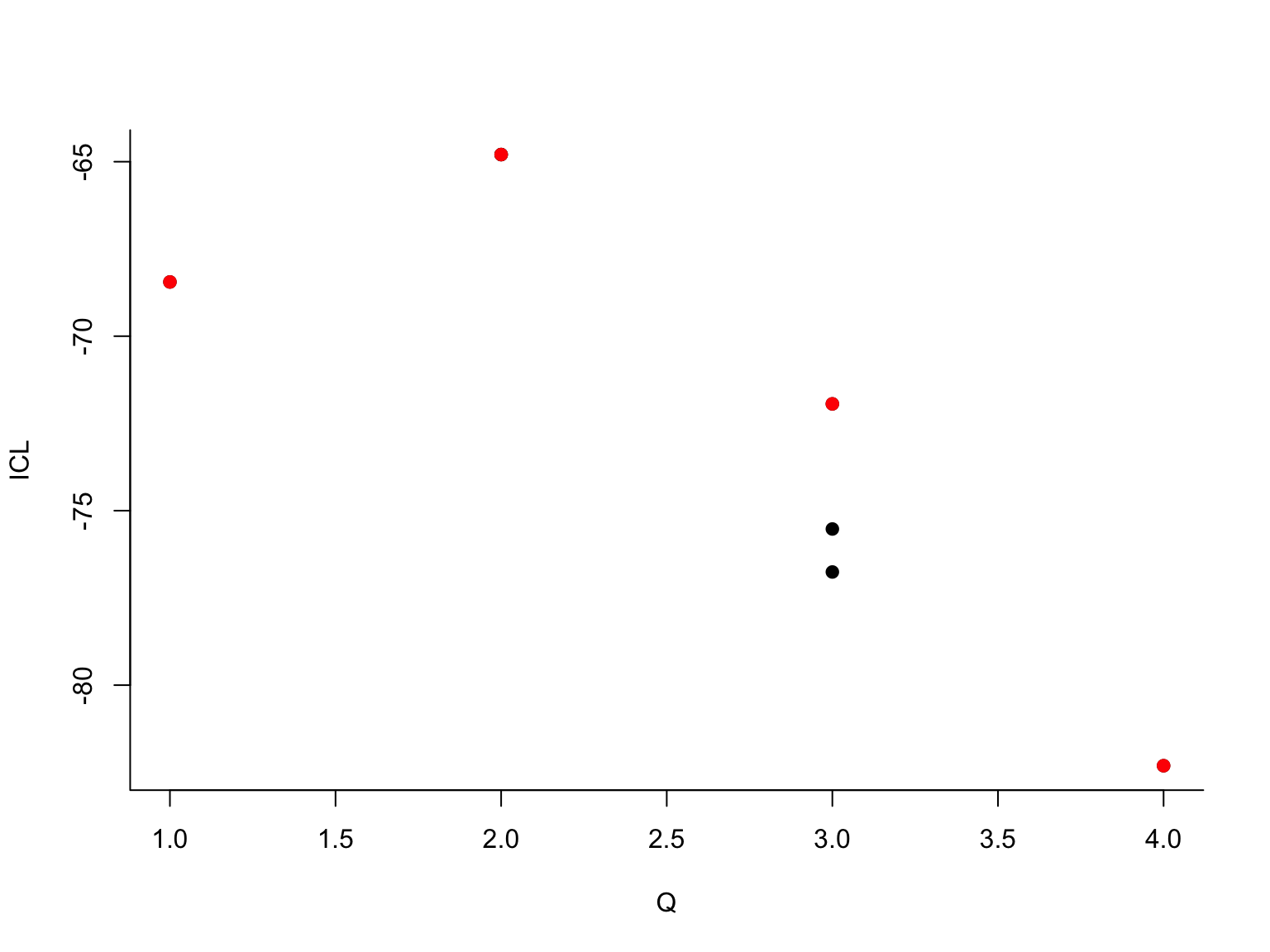
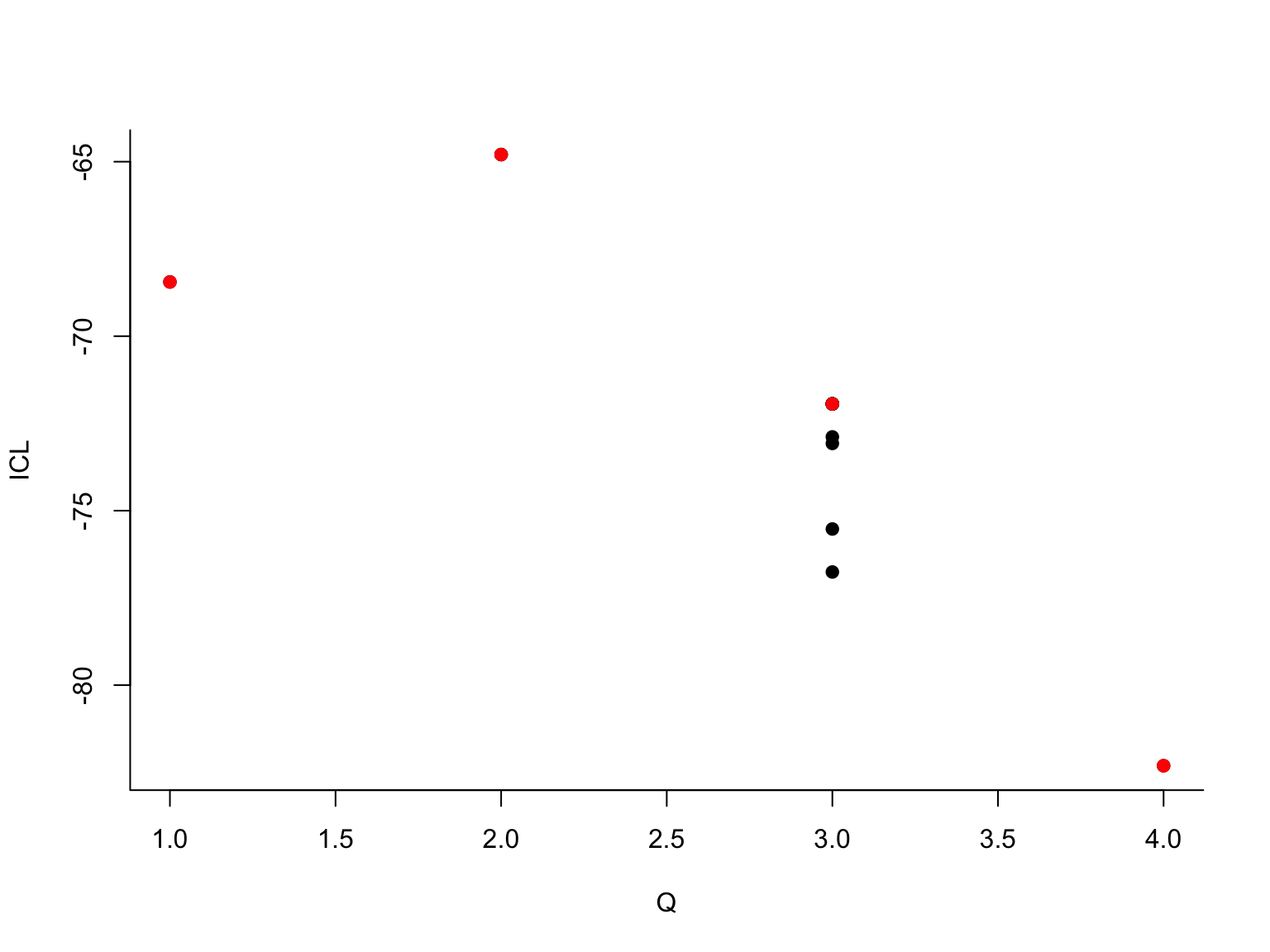
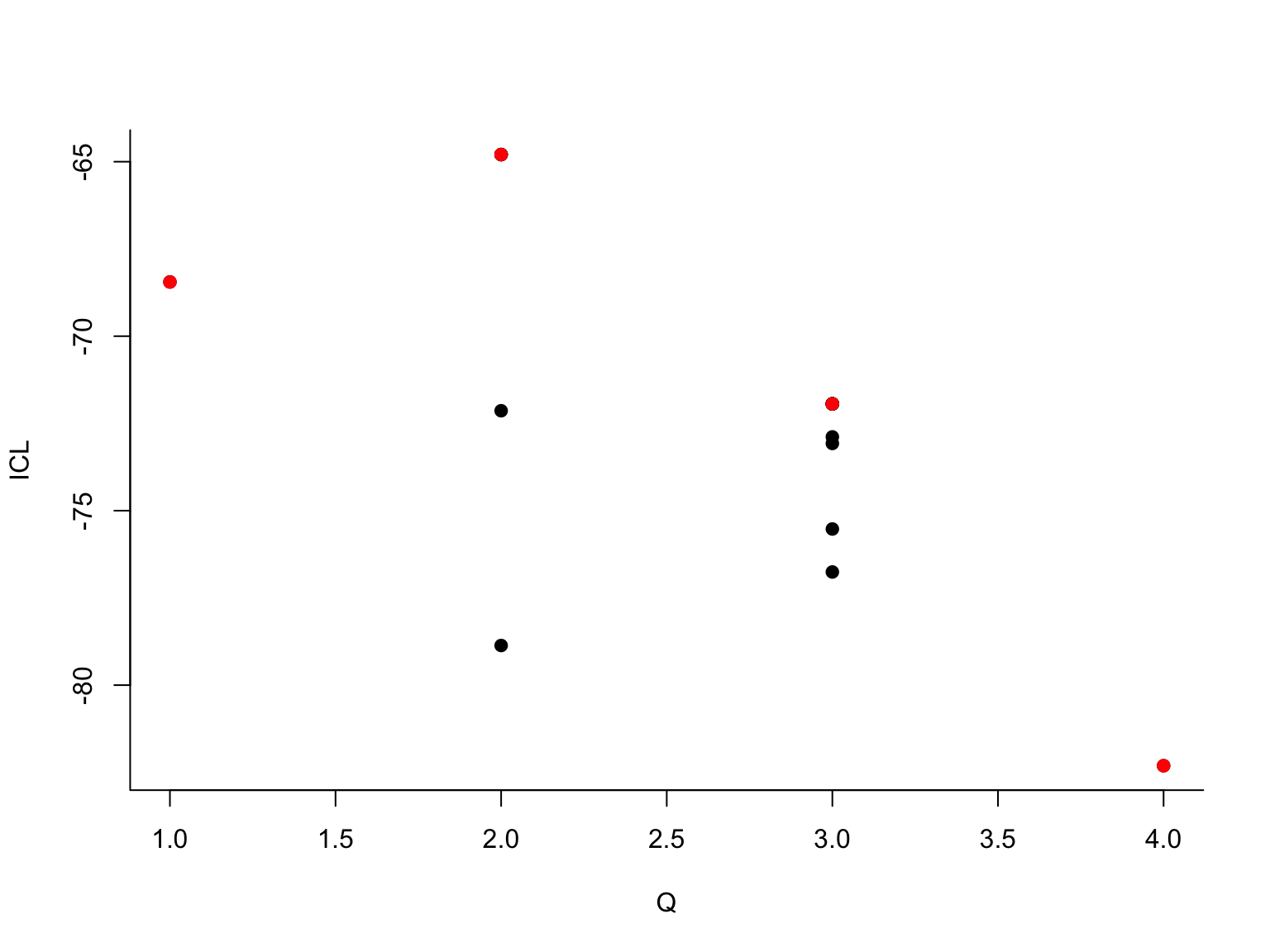
##         -> For 2 groups

Les différents graphiques montrent comment l’algorithme VEM explore les modèles à des nombres de groupes \(Q\) différents : en commençant à \(Q=1\), l’algorithme explore au fur et à mesure tous les modèles jusqu’à \(Q=4\) (les 4 premiers graphiques). Pour chaque valeur de \(Q\) le point rouge représente la valeur du critère ICL correspondant. Ensuite, l’algorithme repart en arrière : l’algorithme VEM est relancé pour tous les modèles de \(Q=4\) à \(Q=1\). D’autres solutions sont trouvées et représentées par des nouveaux points dans les graphiques. Le maximum (actuel) en rouge, les maxima locaux en noir. Ce qui se cache derrière est une stratégie élaborée d’initialisation de VEM. On se sert, par exemple, de la solution à \(Q+1\) groupes pour initialiser l’algorithme à \(Q\) groupes (en fusionnant des groupes), ou, dans une passe ascendante, on utilise la solution à \(Q-1\) groupes pour initialiser le modèle à \(Q\) groupes (en coupant un groupe en deux). En fonction des données, la méthode va effectuer plusieurs passes et, si besoin, explorer des modèles avec plus de 4 groupes, jusqu’à obtenir une courbe ICL bien lissée.

En fait, les résultats de l’algorithme VEM sont très sensibles à l’intialisation et une stratégie d’intialisation sophisitiquée est nécessaire pour trouver l’estimateur de maximum de vraisemblance. Et même avec de nombreuses intialisations, on ne peut jamais être sûr d’avoir trouvé le maximum global.

On peut afficher les valeurs de l’ICL pour les différents modèles :

mySimpleSBM$storedModels
##   nbParams nbBlocks       ICL    loglik
## 1        1        1 -68.44629 -66.11931
## 2        4        2 -64.79549 -56.46052
## 3        8        3 -71.94030 -55.27037
## 4       13        4 -82.30910 -54.97722

ou encore tracer la courbe ICL :

library(ggplot2)
mySimpleSBM$storedModels %>% 
  ggplot() + 
    aes(x = nbBlocks, y = ICL) + 
    geom_line() + 
    geom_point(alpha = 0.5)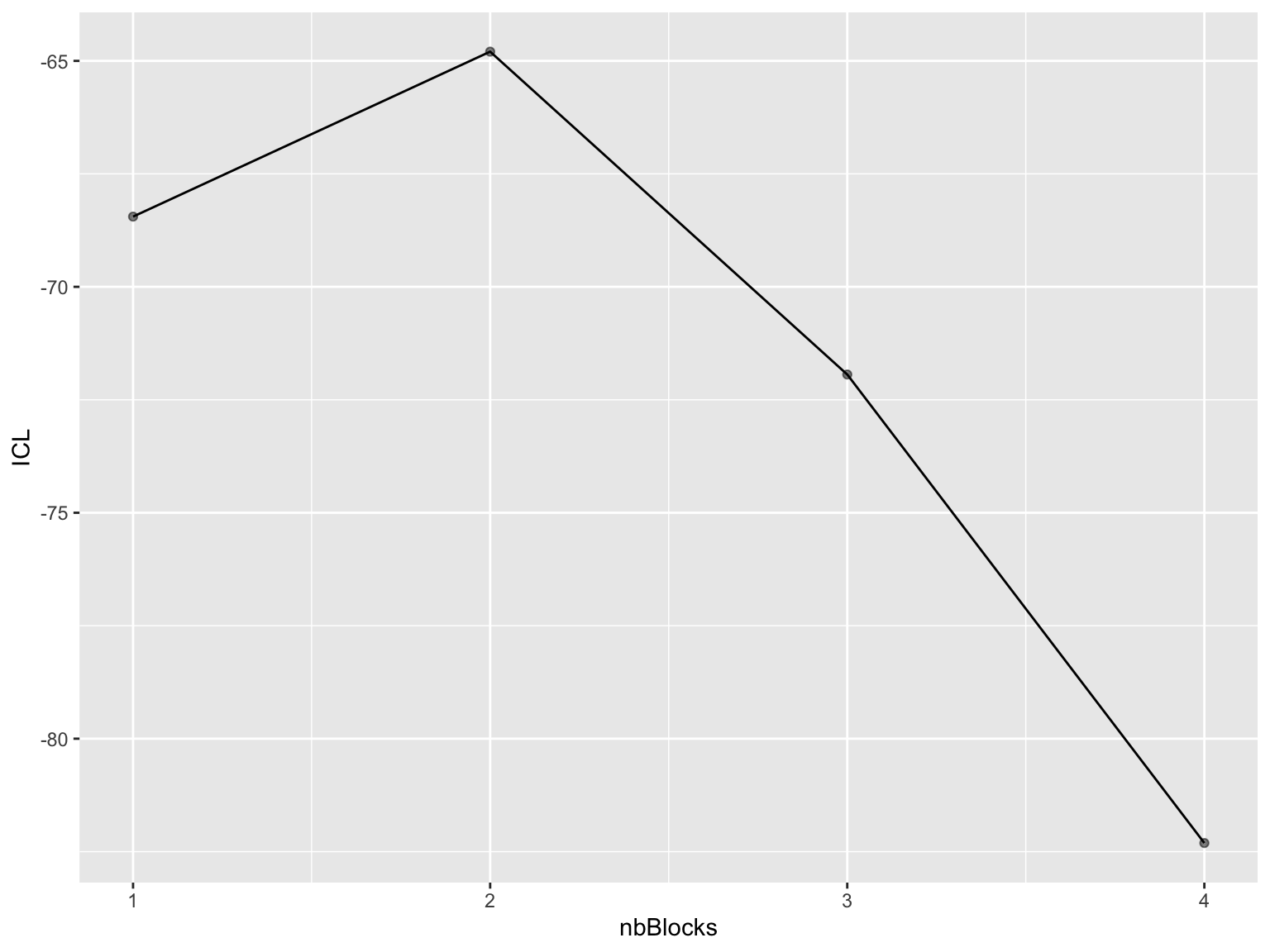

Le maximum est bien atteint en \(Q=2\).

Afin d’étudier un autre modèle que celui qui maximise l’ICL on utilise la méthode setModel :

mySimpleSBM$setModel(3)
mySimpleSBM$nbBlocks
## [1] 3
mySimpleSBM$plot(type = 'data')

mySimpleSBM$plot(type = 'expected')

# les proportions de groupe :
coef(mySimpleSBM, 'block')
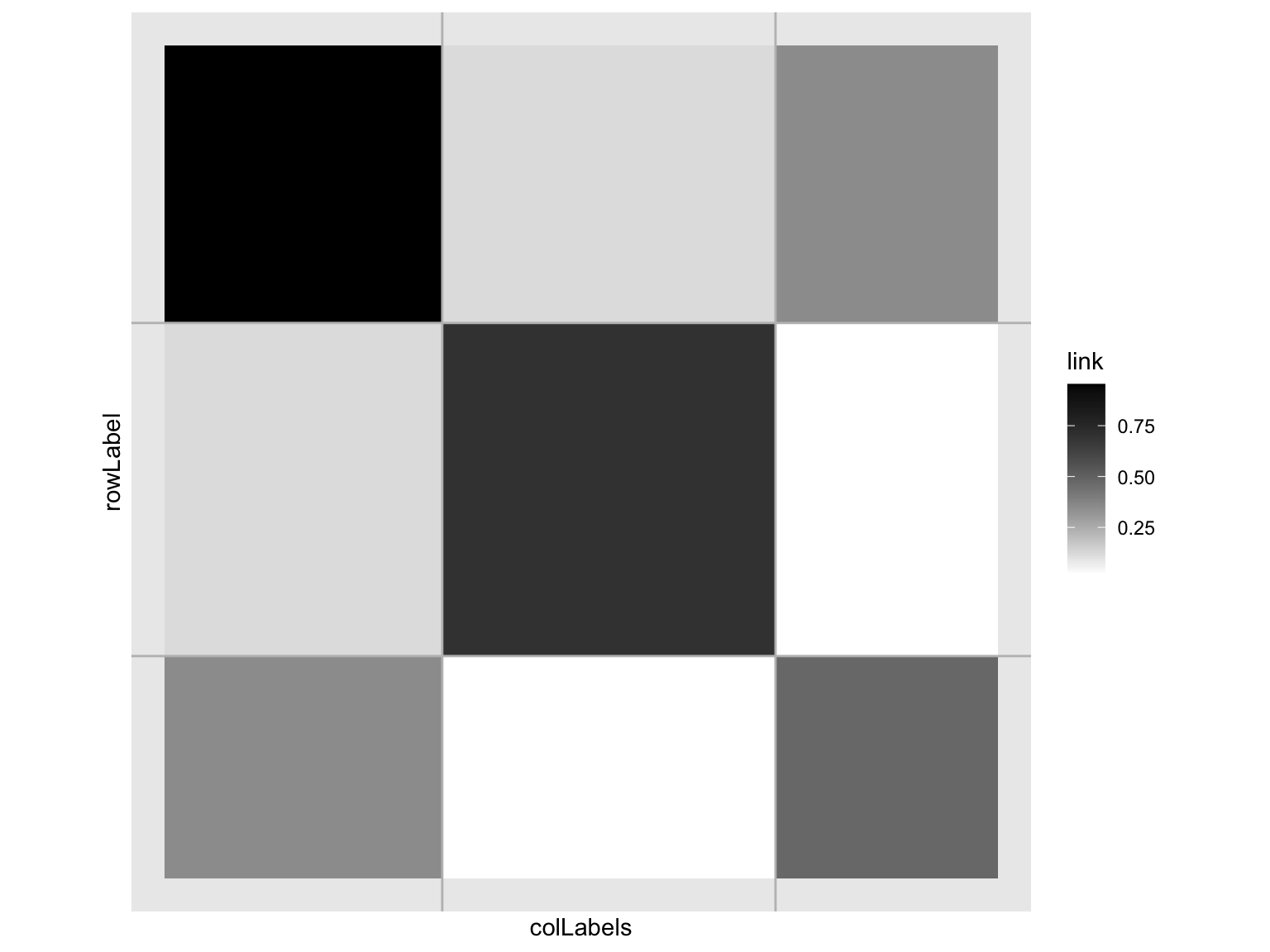
## [1] 0.3333333 0.3986755 0.2679912
# les paramètres de connectivité
coef(mySimpleSBM, 'connectivity')
## $mean
##           [,1]       [,2]       [,3]
## [1,] 0.9738960 0.10868638 0.34963168
## [2,] 0.1086864 0.71732674 0.01041297
## [3,] 0.3496317 0.01041297 0.48398979

Comparons les clusterings trouvés à \(Q=2\) et à \(Q=3\) groupes :

# clustering du modèle actuel à Q=3 groupes :
clustQ3 <- mySimpleSBM$memberships
clustQ3
##  [1] 2 3 1 1 2 1 2 2 3 1 2 1 2 3 3
# remettre le modèle actuel à Q=2 :
mySimpleSBM$setModel(2)
clustQ2 <- mySimpleSBM$memberships
clustQ2
##  [1] 2 1 1 1 2 1 2 2 1 1 2 1 2 1 1
# comparer les deux clusterings :
table(clustQ3, clustQ2)
##        clustQ2
## clustQ3 1 2
##       1 5 0
##       2 0 6
##       3 4 0

On observe que le groupe 1 du modèle à deux groupes à été divisé en deux groupes (les groupes 1 et 3 du modèle à trois groupes). L’ICL juge que ce n’est pas pertinent de travailler avec le modèle affiné et qu’il faut privilégier le modèle à deux groupes.

Exercice 2

  1. Reprenez un des graphes simulés à l’exercice précédent et ajuster un SBM aux données. Retrouve-t-on les bonnes valeurs des paramètres ? et le clustering d’origine ?

  2. Considérons le modèle à blocs stochastiques au paramètres suivants : \(Q=4\) groupes, \(\boldsymbol\pi=(1/4,1/4,1/4,1/4)\) et \[\boldsymbol \gamma=\left(\begin{array}{llll} 0.2& 0.7&0.1&0.5\\ 0.7&0.7&0.1&0.5\\ 0.1&0.1&0.9&0.5\\ 0.5&0.5&0.5&0.1 \end{array}\right).\] Générer un graphe à \(n=20\) noeuds et ajuster un SBM sur les données. Qu’observez-vous? Que se passe-t-il quand on augmente le nombre de noeuds?

  3. Appliquer le spectral clustering normalisé et le spectral clustering avec \(L_{\text{abs}}\) aux graphes de la question précédente. Retrouve-t-on les bons groupes?

  4. Reprendre le petit jeu de données karate du TP1. Ajuster un modèle SBM pour faire un clustering des noeuds. Appliquer les algorithmes de spectral clustering normalisé et avec \(L_{\text{abs}}\), et comparer les clustering obtenus.