7.4 Modèles graphiques

Un modèle graphique est une représentation ou visualisation de la structure des dépendances conditionnelles des variables aléatoires d’un modèle probabiliste par un graphe. Dans ce graphe, chaque noeud représente une variable aléatoire du modèle et les arêtes représentent des dépendances entre ces variables.

Remarquons que la terminologie “modèle graphique” n’a rien à voir avec des données organisées sous forme de graphes. Les variables aléatoires \(X_i\) ne traduisent pas des interactions entre des entités. Le graphe est un objet abstrait qui structure la dépendance entre les variables aléatoires. N’importe quel modèle probabiliste à plusieurs variables aléatoires peut être représenté par un modèle graphique.

Il existe deux types de modèles graphiques: des modèles dirigés et non dirigés. Deux exemples importants de modèles graphiques sont les réseaux bayésiens, qui donnent des graphes orientés acycliques, et les champs aléatoires de Markov qui sont non orientés.

On pourra se référer à Lauritzen (1996) ou au Chapitre 8 de Bishop (2006) pour en savoir plus.

7.4.1 Modèle graphique dirigé

Avant de donner la définition générale d’un modèle graphique dirigé, considérons quelques exemples.

Par la règle de Bayes, toute loi jointe \(\mathbb P\) d’un vecteur aléatoire \(\mathbf X=(X_1,\dots,X_d)\) peut s’écrire comme \[\begin{align} \mathbb P(X_1,\dots,X_d) &=\mathbb P(X_d|X_1,\dots,X_{d-1})\mathbb P(X_1,\dots,X_{d-1})\notag\\ &=\mathbb P(X_d|X_1,\dots,X_{d-1})\mathbb P(X_{d-1}|X_1,\dots,X_{d-2})\dots \mathbb P(X_2|X_1)\mathbb P(X_1). \tag{7.2} \end{align}\] Cette factorisation de la loi jointe en produit de lois conditionnelles peut être représentée par une graphe dirigé, appelé un modèle graphique dirigé (Figure 7.2).

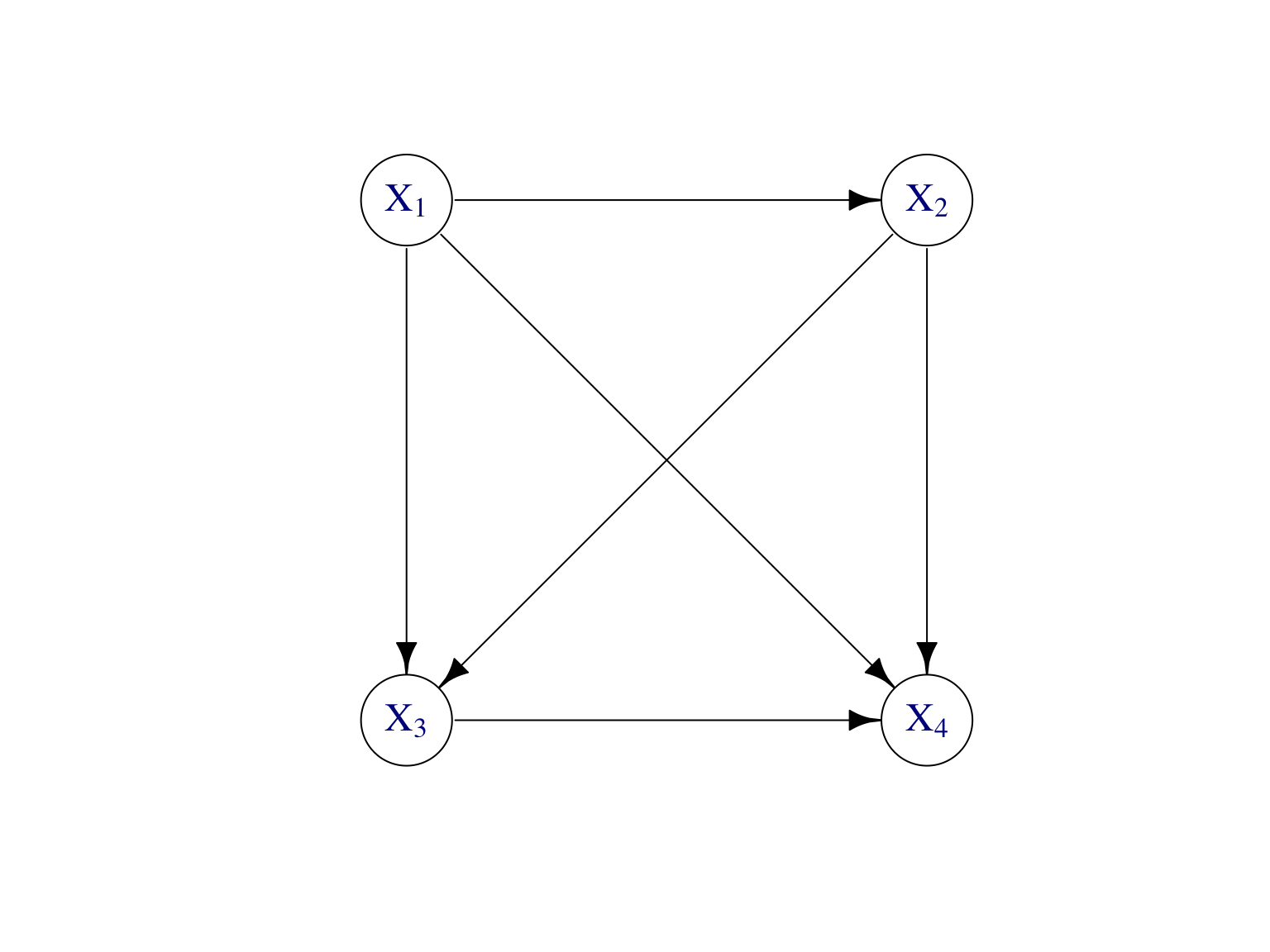
Figure 7.2: Modèle graphique dirigé pour représenter la factorisation de loi jointe donnée par (7.2) de n’importe quelle vecteur aléatoire \((X_1,\dots,X_4)\) de dimension \(d=4\).

Or, la factorisation en (7.2) n’est pas unique. On a aussi bien \[\begin{align} \mathbb P(X_1,\dots,X_d) &=\mathbb P(X_1|X_2,\dots,X_{d})\mathbb P(X_{2}|X_3,\dots,X_{d})\dots \mathbb P(X_{d-1}|X_d)\mathbb P(X_d), \tag{7.3} \end{align}\] Cette factorisation est représentée en Figure 7.3.

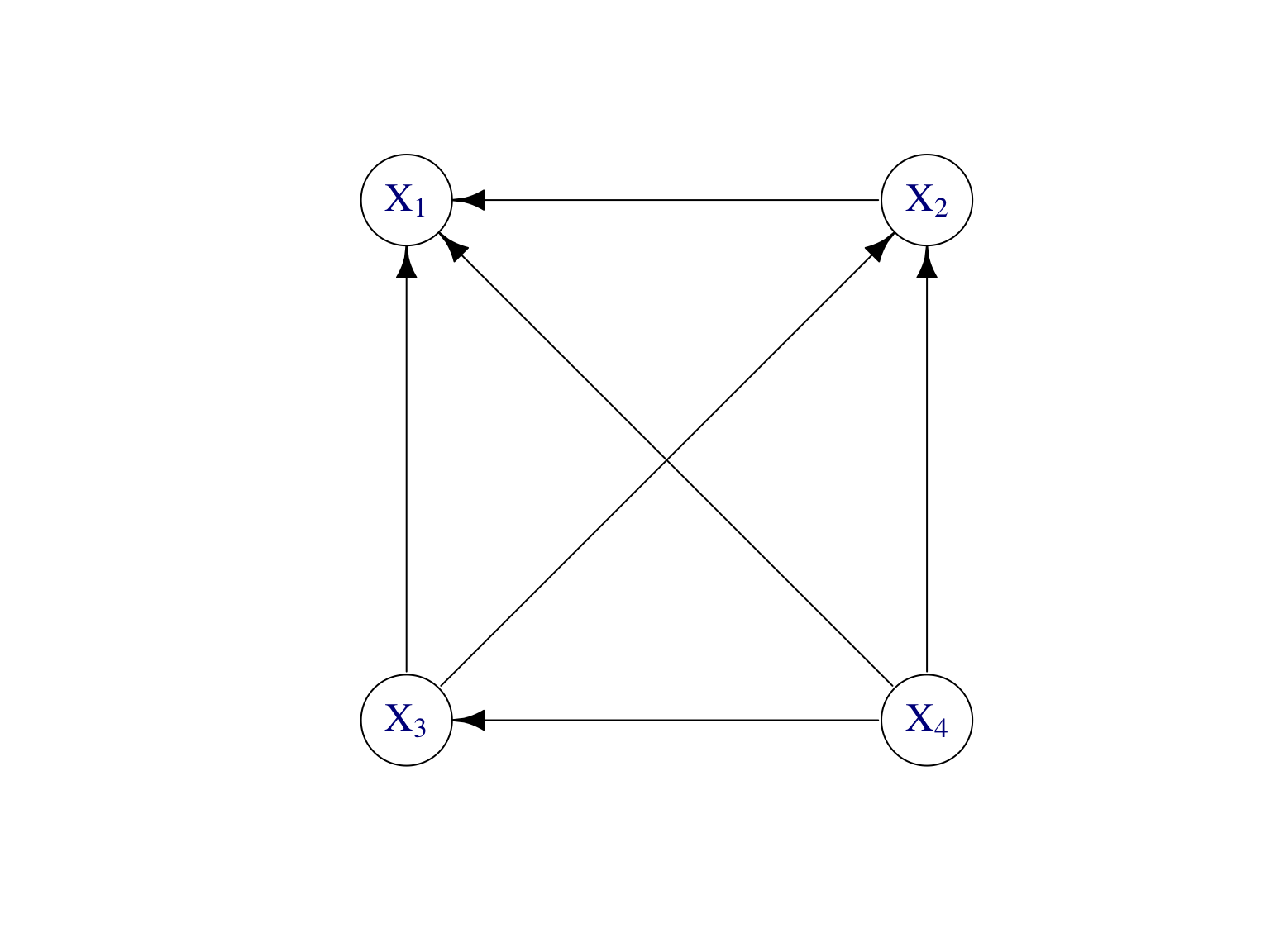
Figure 7.3: Modèle graphique dirigé pour représenter la factorisation de loi jointe donnée par (7.3) de n’importe quelle vecteur aléatoire \((X_1,\dots,X_4)\) de dimension \(d=4\).

Tout modèle graphique dirigé est un graphe orienté acyclique ou DAG (pour directed acyclic graph), i.e. il ne possède pas de cycle dirigé.

Les factorisations en (7.2) et (7.3) sont vraies pour toute loi de probabilité. Les modèles graphiques en Figure 7.2 et 7.3 sont alors dits complets ou fully connected.

L’absence d’arêtes dans le modèle graphique dirigé traduit des propriétés d’indépendences entre les variables.

Exemple. Soit \(X_2\) indépendant de \((X_3,X_4)\), alors \[\begin{align} \mathbb P(X_1,\dots,X_4) &=\mathbb P(X_1|X_2,X_3,X_{4})\mathbb P(X_{2}) \mathbb P(X_{3}|X_4)\mathbb P(X_4). \tag{7.4} \end{align}\] Le modèle graphique dirigé correspondant est donné par la Figure 7.4.

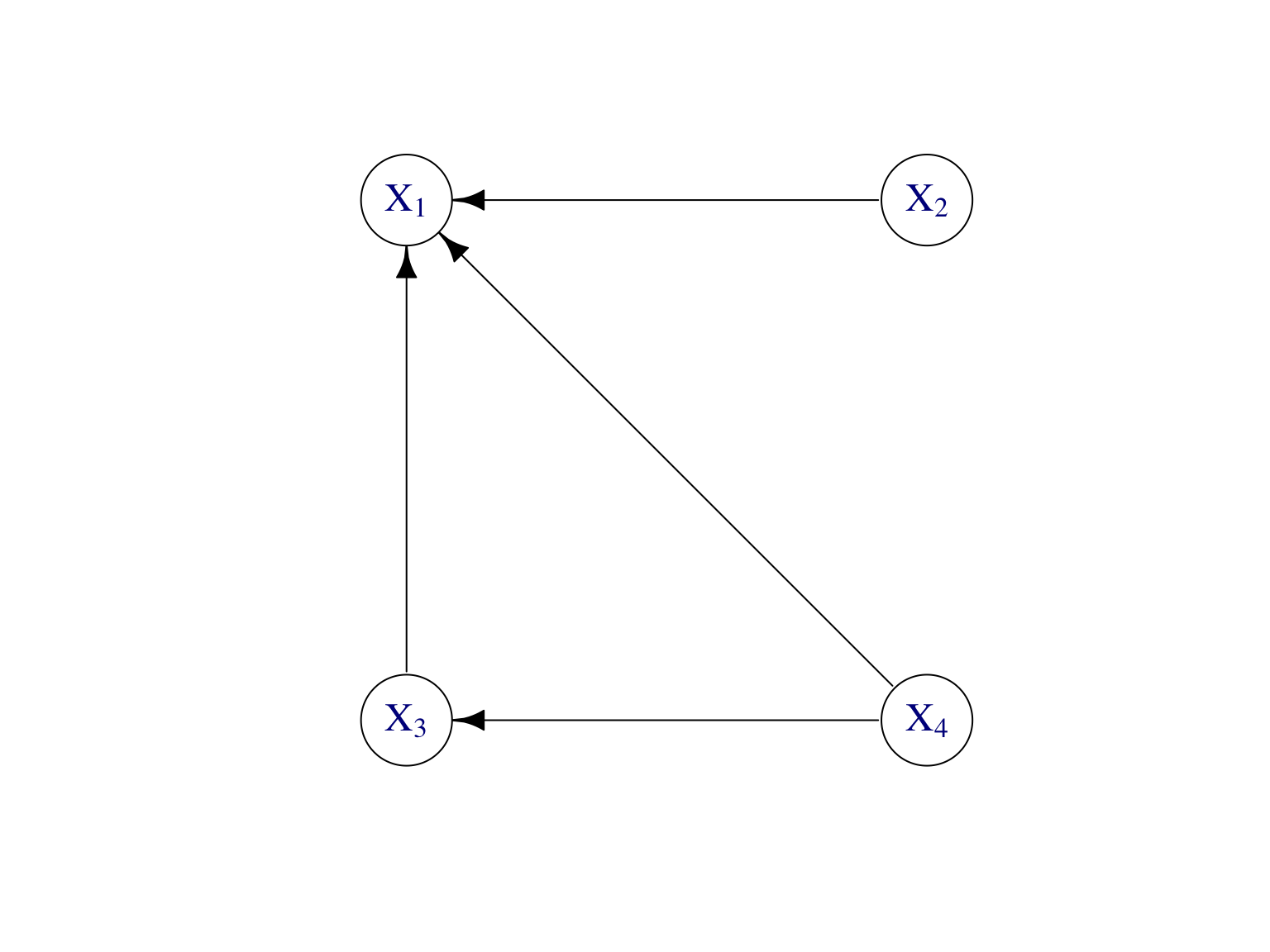
Figure 7.4: Modèle graphique dirigé pour représenter la factorisation de loi jointe donnée par (7.4) lorsque \(X_2\) est indépendant de \((X_3,X_4)\).

Definition 7.1 (Modèle graphique dirigé) Soit \(\mathbf X=(X_1,\dots,X_d)\) un vecteur aléatoire de loi jointe \(\mathbb P\). Un graphe \(G=(V,E)\) dirigé dont l’ensemble de noeuds \(V=\{X_1,\dots,X_d\}\) représente les variables aléatoires est un modèle graphique dirigé associé à la loi jointe \(\mathbb P\) de \(\mathbf X\) si \(\mathbb P\) se factorise selon le graphe \(G\), i.e. \[ \mathbb P(X_1,\dots,X_d) =\prod_{i=1}^d\mathbb P(X_i|\textrm{pa}(X_i)), \] où \(\textrm{pa}(X_i)=\{j\in V:(j,i)\in E\}\) désigne l’ensemble des parents de \(i\) dans \(G\).

 

Comme déjà mentionné, le graphe \(G\) n’est pas unique en général. Par exemple, si il n’y a pas de contrainte sur \(\mathbb P\), on a \[\begin{align*} \mathbb P(X_1,X_2,X_3) &=\mathbb P(X_3|X_1,X_2)\mathbb P(X_2|X_1)\mathbb P(X_1)\\ &=\mathbb P(X_{\sigma(3)}|X_{\sigma(1)},X_{\sigma(2)})\mathbb P(X_{\sigma(2)}|X_{\sigma(1)})\mathbb P(X_{\sigma(1)}), \end{align*}\] pour toute permutation \(\sigma\).

Exercice Ecrire la loi jointe de \((X_1,\dots,X_7)\) donnée par le modèle graphique dirigé de la Figure 7.5.

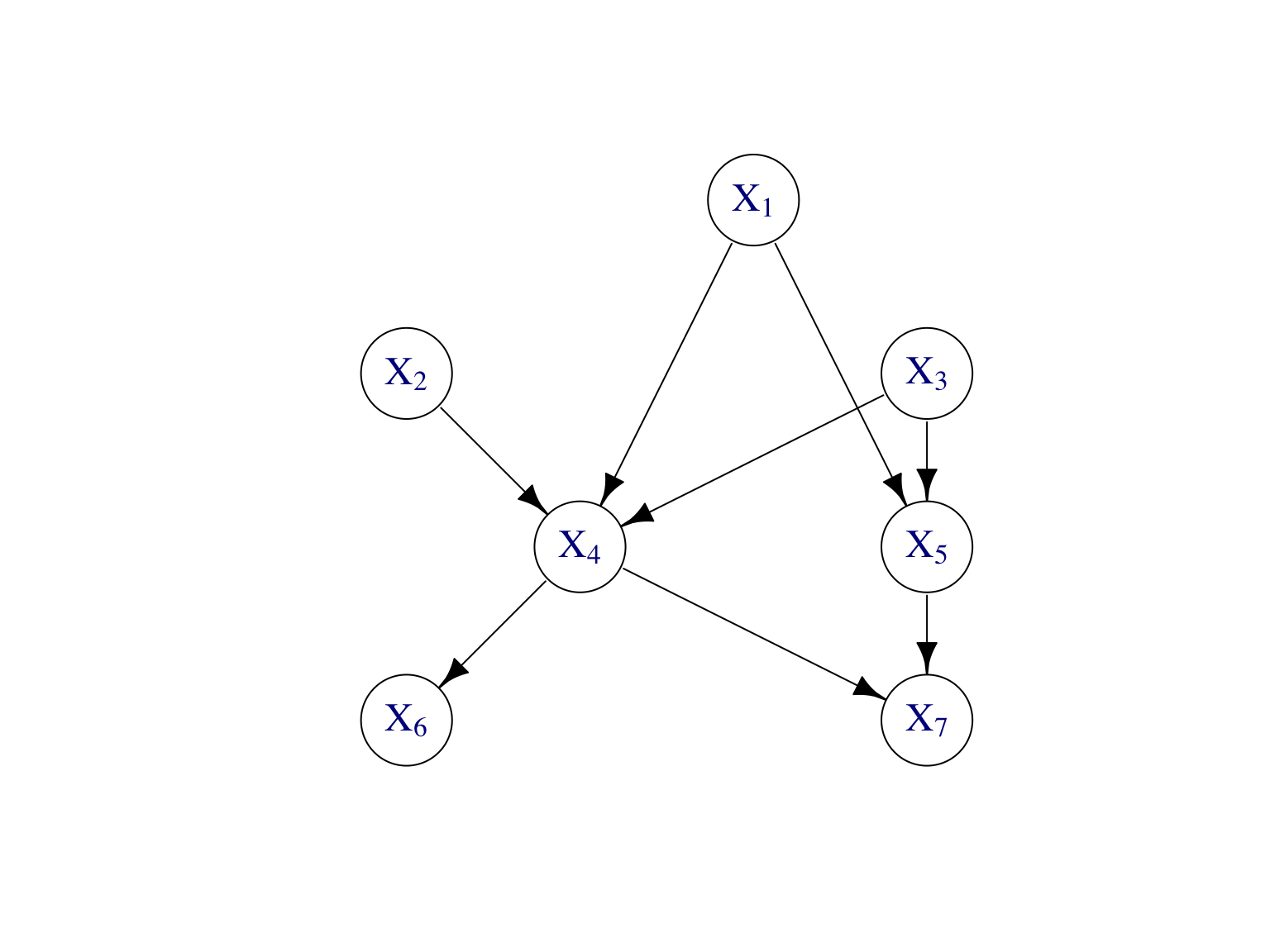
Figure 7.5: Modèle graphique dirigé pour représenter la factorisation de la loi jointe \(\mathbb P\) d’un vecteur aléatoire \((X_1,\dots,X_7)\) de dimension \(d=7\).

 

Les modèles graphiques dirigés sont beaucoup utilisés pour visualiser des modèles bayésiens.

Exemple d’un modèle bayésien. Soit \(\mathbf X=(X_1,\dots,X_n)\) un échantillon de la loi normale \(\mathcal N(\mu,\sigma^2)\). On suppose que les paramètres \(\mu\) et \(\sigma^2\) sont des variables aléatoires de loi a priori \(\mu\sim \mathcal N(\tau,\nu^2)\) et \(\lambda=1/\sigma^2\sim\text{Gamma}(\alpha,\beta)\). Les paramètres \(\tau,\nu,\alpha,\beta\) sont les hyperparamètres du modèle. On dit que ce modèle est hiérarchique et on le représente par un DAG, cf. Figure 7.6. Ces modèles sont pratique pour la simulation.

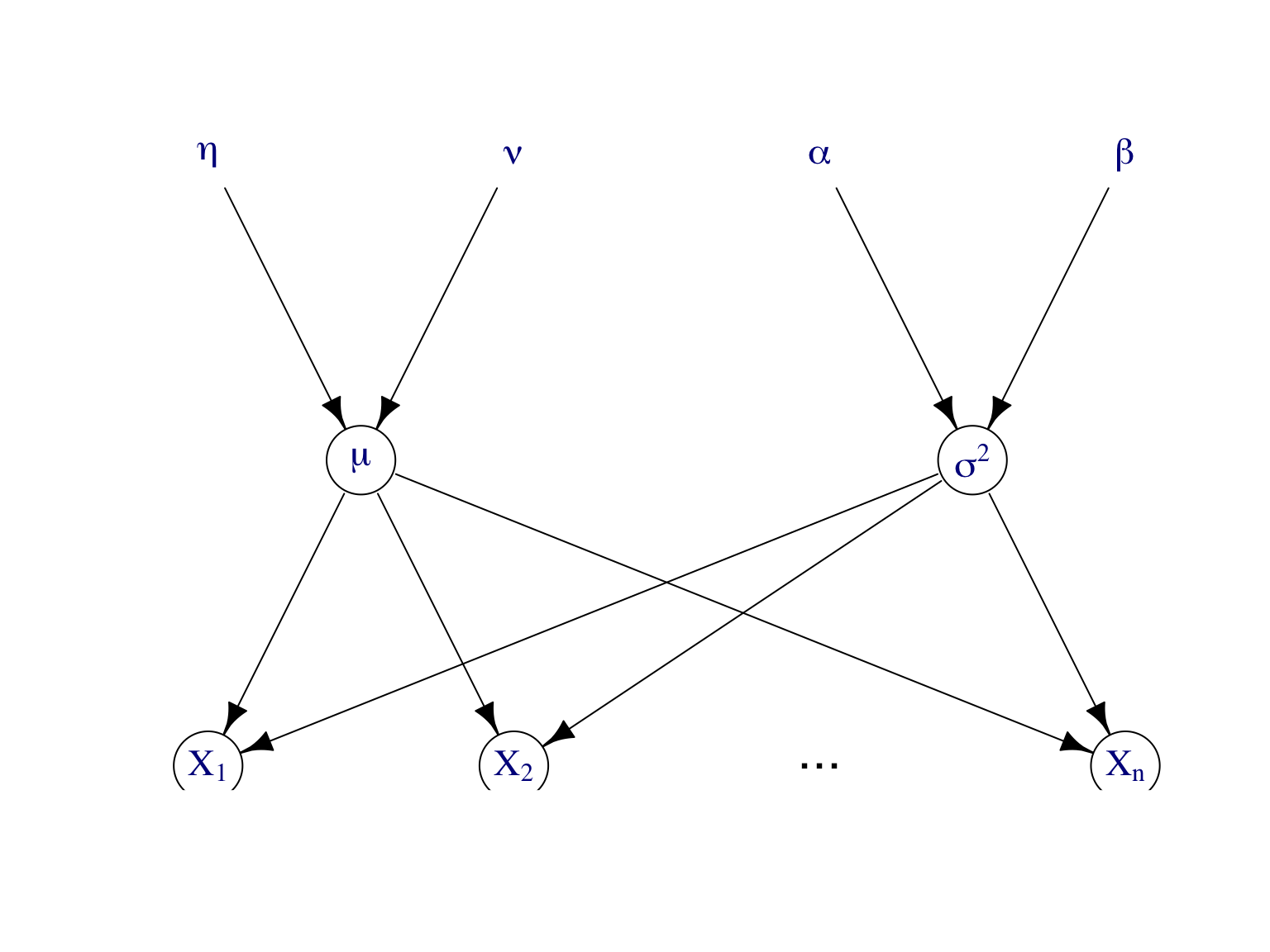
Figure 7.6: Modèle graphique dirigé pour représenter le modèle bayésien de l’exemple.

7.4.2 Modèle graphique non dirigé

Definition 7.2 (Modèle graphique non dirigé) Un graphe \(G=(V,E)\) non dirigé est un modèle graphique non dirigé associé à la loi jointe \(\mathbb P\) de \(\mathbf X=(X_1,\dots,X_d)\) si pour toute arête absente dans le graphe \(\{i,j\}\notin E\), les variables aléatoires \(X_i\) et \(X_j\) sont indépendantes conditionnellement à toutes les autres variables \(X_{V\backslash\{i,j\}}\), à savoir \[\begin{align} \mathbb P(X_i, X_j| X_{V\backslash\{i,j\}}) =\mathbb P(X_i| X_{V\backslash\{i,j\}})\mathbb P( X_j| X_{V\backslash\{i,j\}}). \tag{7.5} \end{align}\]

 

Notons que (7.5) est équivalent à \[ \mathbb P(X_i| X_j, X_{V\backslash\{i,j\}}) =\mathbb P(X_i| X_{V\backslash\{i,j\}}). \]

D’après (7.2), toute loi \(\mathbb P\) de \(\mathbf X=(X_1,\dots,X_d)\) se factorise de la façon \[\begin{align*} \mathbb P(X_1,\dots,X_d) &=\mathbb P(X_d|X_1,\dots,X_{d-1})\mathbb P(X_{d-1}|X_1,\dots,X_{d-2})\dots \mathbb P(X_2|X_1)\mathbb P(X_1)\\ &=\Psi_1(X_1,\dots,X_d)\Psi_2(X_2,\dots,X_d)\dots \Psi_{d-1}(X_1,X_2), \end{align*}\] avec des fonctions \(\Psi_k\). A partir de cette écriture, on définit un graphe non dirigé en mettant tous les noeuds qui apparaissent dans une fonction \(\Psi_k\) dans une clique. Ceci donne le modèle graphique non dirigé complet associé à la loi \(\mathbb P\), cf. Figure 7.7.

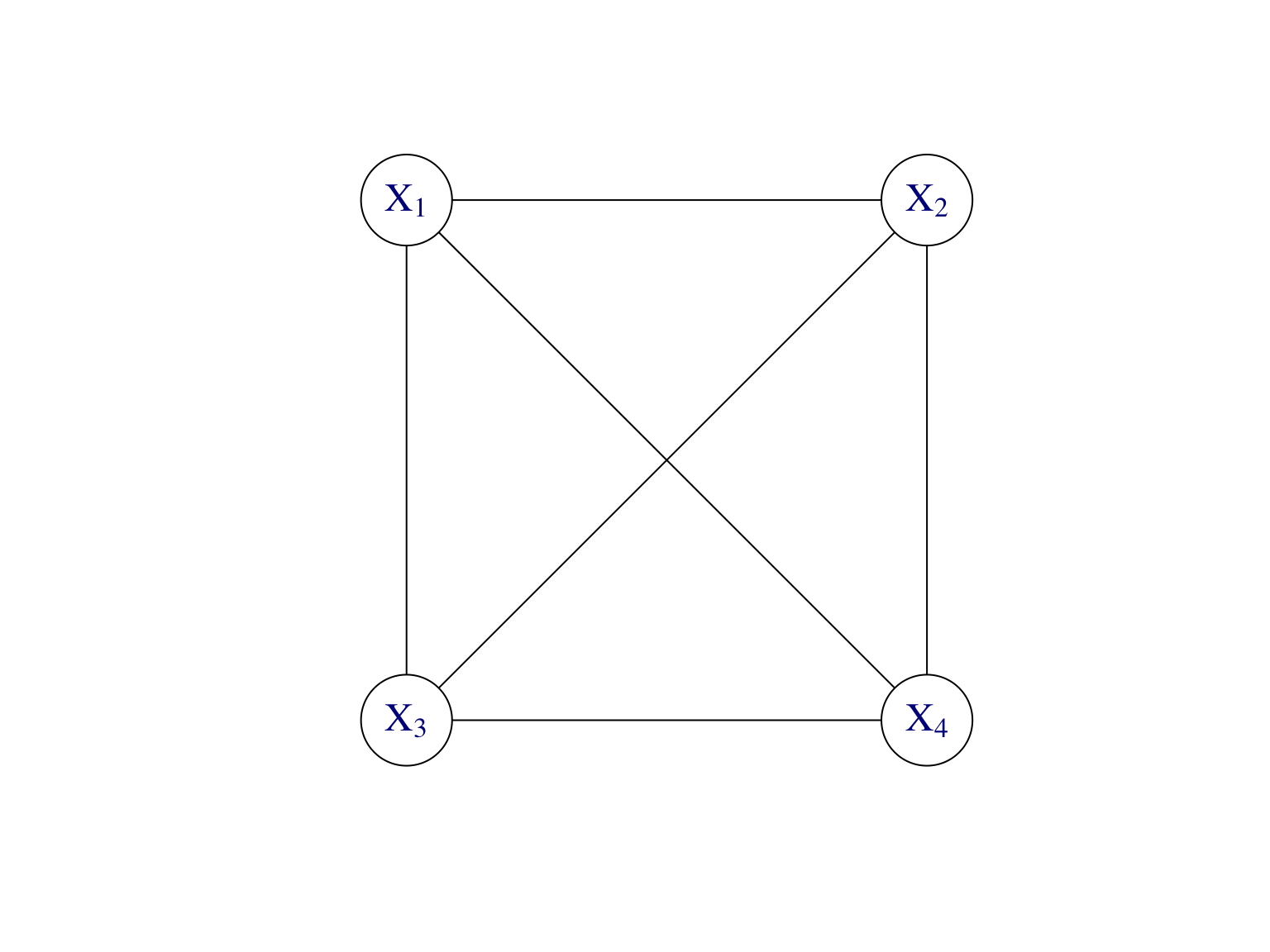
Figure 7.7: Modèle graphique non dirigé pour représenter la loi jointe de n’importe quel vecteur aléatoire \((X_1,\dots,X_4)\) de dimension \(d=4\).

Exemple Supposons que \[\mathbb P(X_1,\dots,X_4)=\mathbb P(X_4|X_3)\mathbb P(X_3|X_1,X_2)\mathbb P(X_2)\mathbb P(X_1).\] Les modèles graphiques correspondants, dirigé et non dirigé, sont donnés par la Figure 7.8.

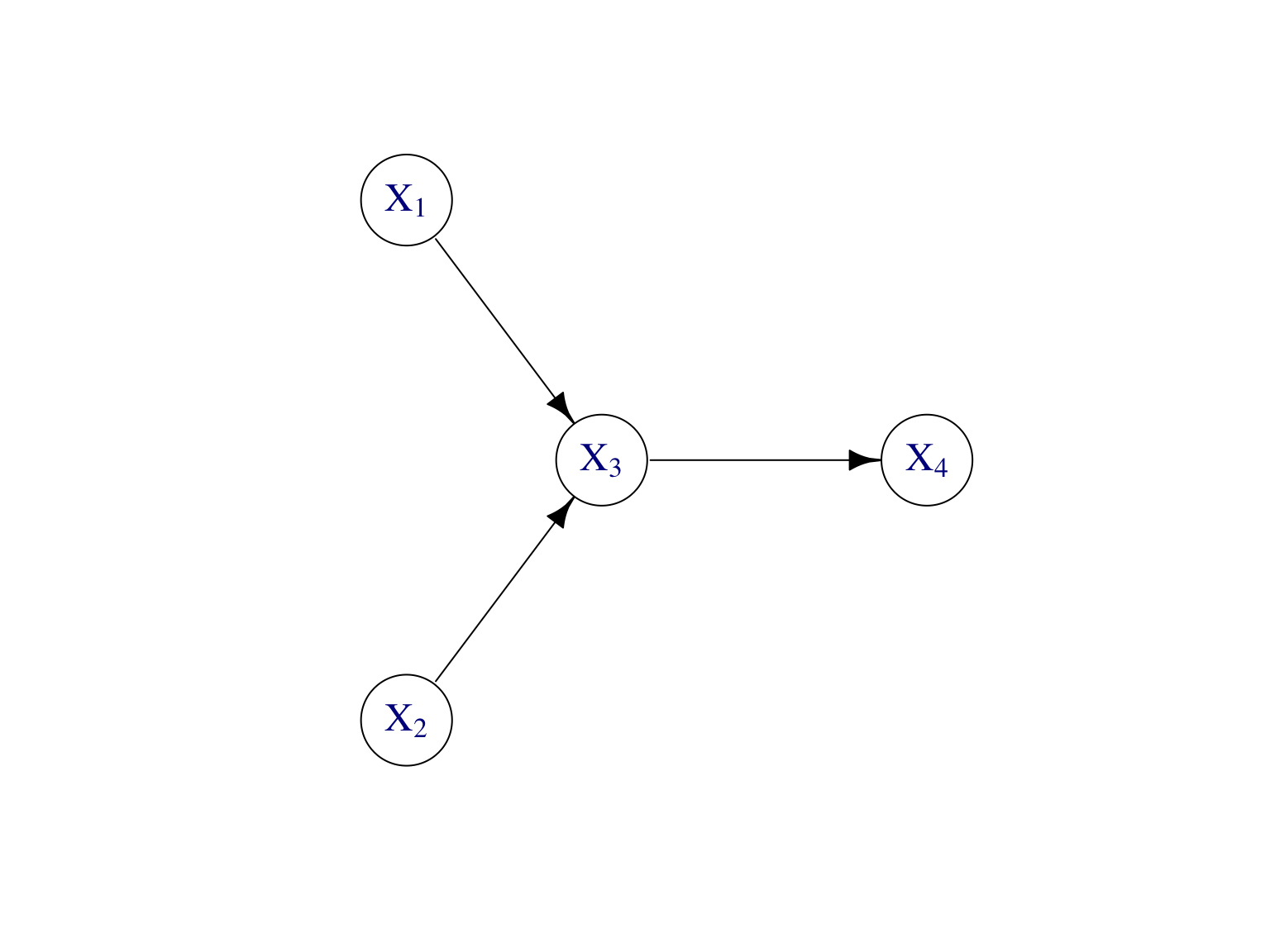
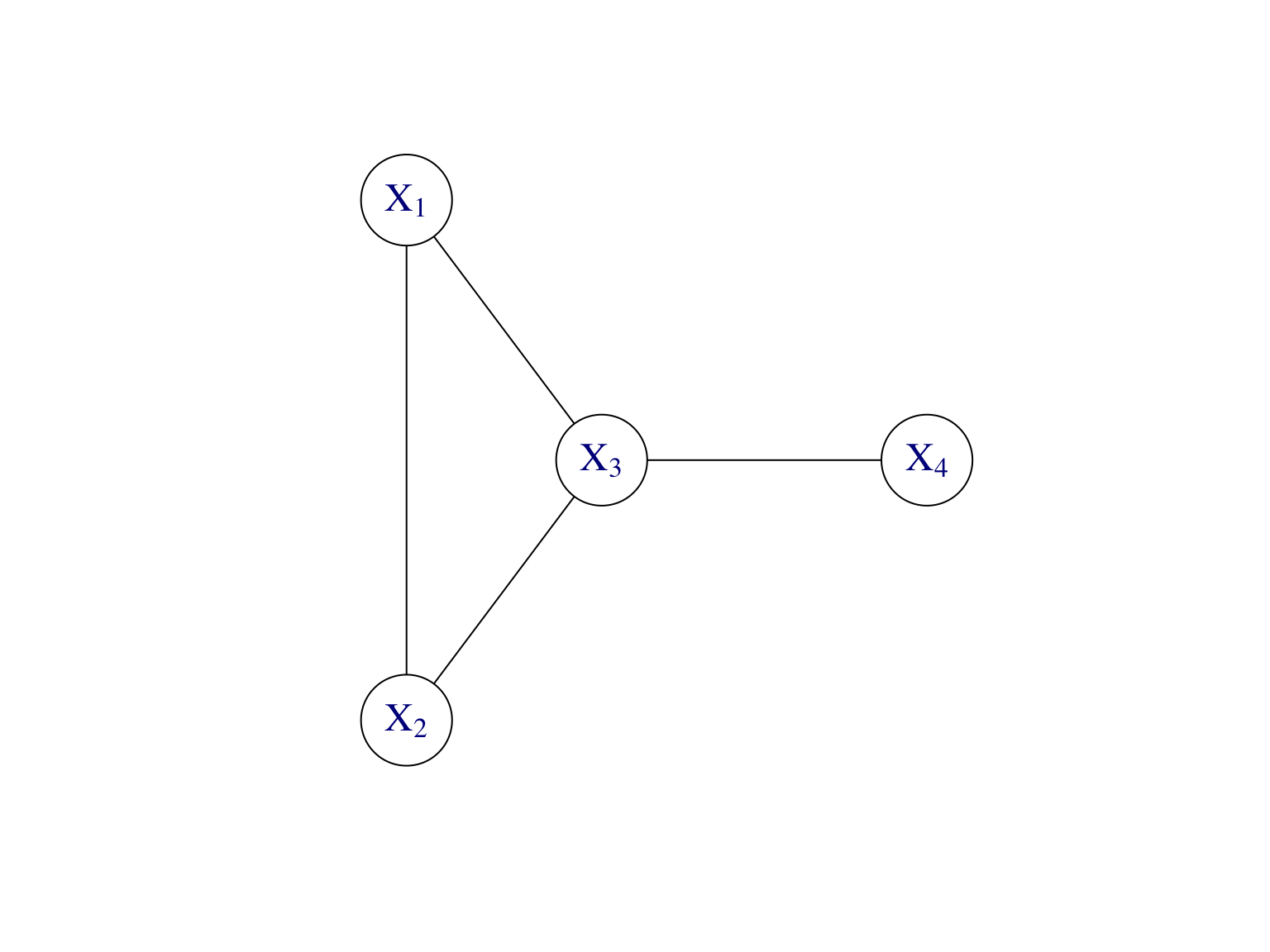
Figure 7.8: Modèles graphiques, dirigé et non dirigé, de l’exemple.

7.4.3 Graphe moral

Le modèle graphique dirigé n’est pas forcément unique. En revanche, le modèle graphique non dirigé pour la même loi \(\mathbb P\) l’est. La construction du modèle graphique non dirigé à partir du dirigé s’appelle la moralisation du graphe et le graphe obtenu est dit le graphe moral.

On obtient le graphe moral en connectant les parents de tous les noeuds entre eux, i.e. on relie les parents par des arêtes, puis on retire les directions des arêtes pour obtenir un graphe non orienté. On voit bien qu’on obtient le graphe à gauche dans la Figure 7.8 par moralisation du graphe à droite.

Le terme graphe moral repose sur la vision qu’il est “moral” que les noeuds qui ont un enfant commun soient liés entre eux.

Les modèles graphiques sont utiles pour comprendre les relations d’indépendance entre les variables.

Pour la proposition suivante, introduisons d’abord la notion des descandants d’un noeud \(i\) dans un graphe \(G=(V,E)\) dirigé. On définit \(\mathrm{desc}(i)\) comme l’ensemble de noeuds dans \(V\) tel que \(j\in\mathrm{desc}(i)\) si et seulement si il existe un chemin orienté de \(i\) vers \(j\) dans \(G\).

Proposition 7.1 (Propriétés d’indépendance) Soit \(G=(V,E)\) un modèle graphique.

• Si \(G\) est dirigé, alors conditionnellement à ses parents dans \(G\), une variable est indépendante de ses non-descendants dans \(G\). Autrement dit, si \(K\) est un sous-ensemble de \(V\) tel que \(K\cap \mathrm{desc}(X_i,G) =\emptyset\), alors \[ \mathbb P(X_i| \mathrm{pa}(X_i,G), \{X_k\}_{k \in K}) = \mathbb P(X_i| \mathrm{pa}(X_i,G)). \]
• Soient \(I,J,K\) des sous-ensembles disjoints de \(V\). Si \(G\) est non dirigé, i.e. un graphe morale, et si tous les chemins d’un noeud dans \(I\) à un noeud dans \(J\) passent par un noeud dans \(K\), alors \(\{X_i\}_{i\in I}\) et \(\{X_j\}_{j\in J}\) sont indépendants conditionnellement à \(\{X_k\}_{k\in K}\).

La proposition indique comment lire sur le graphe moral si p.ex. les variables aléatoires \(X_i\) et \(X_j\) sont indépendantes conditionnellement à la variable \(X_k\). Si tous les chemins de \(X_i\) vers \(X_j\) passent par \(X_k\), alors on a bien l’indépendance conditionnelle.

Reprenons les exemples de la Section 7.1.

Exemple. Modèle de mélange. La Figure 7.9 montre le modèle graphique dirigé et son graphe moral d’un modèle de mélange. Rappelons que les \((X_i)_{i\ge 1}\) sont indépendantes et identiquement distribuées, alors que les \((X_i|Z_i)_{i\ge 1}\) sont indépendantes mais pas identiquement distribuées. De même, les \((Z_i|X_i)_{i\ge 1}\) sont indépendantes, ce qui est important pour l’algorithme EM, où on a besoin de la loi aposteriori des variables latentes \((Z_i)_{i\ge 1}\) sachant les observations \((X_i)_{i\ge 1}\).

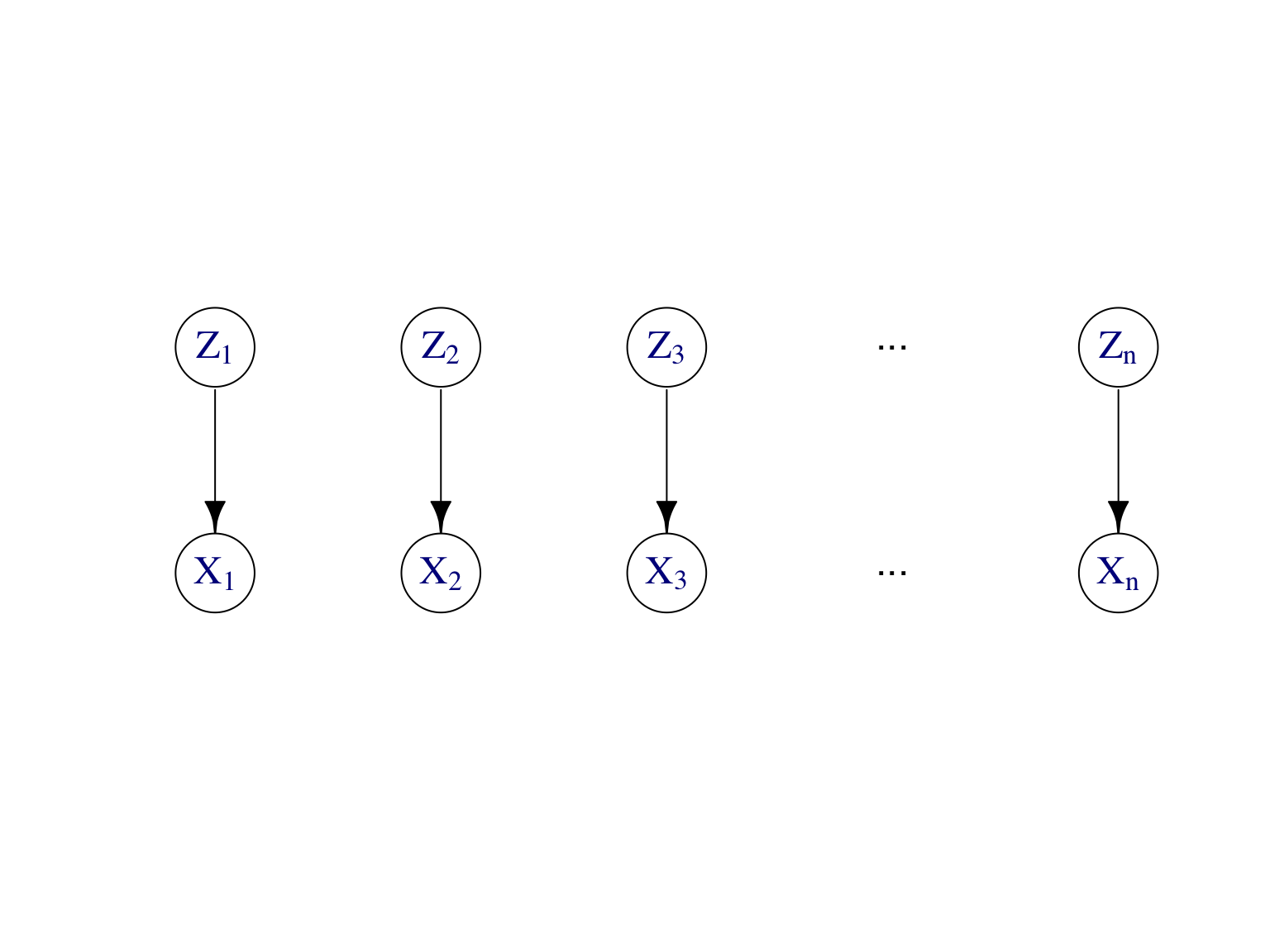
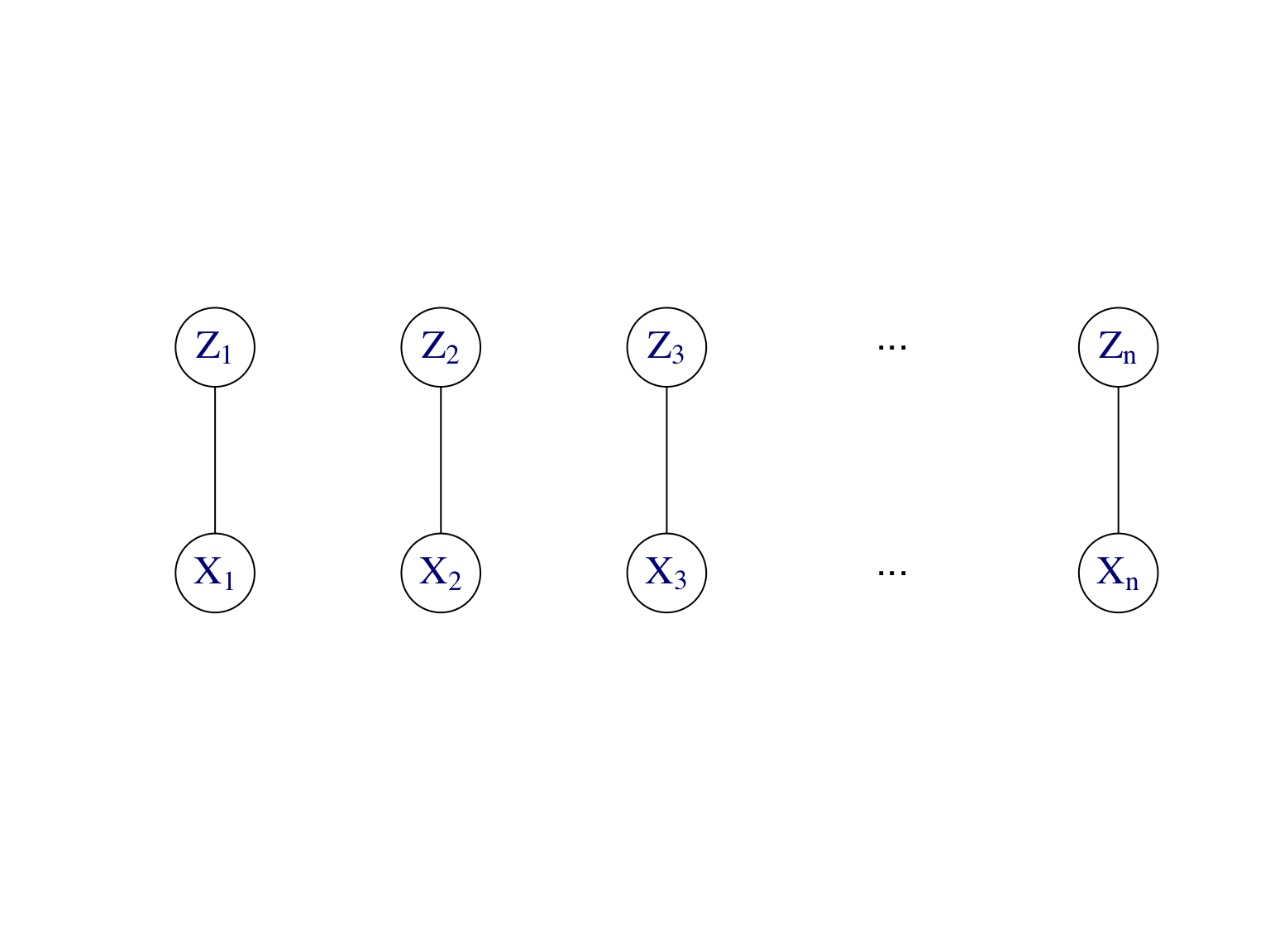
Figure 7.9: Modèle graphique dirigé et son graphe moral d’un modèle de mélange.

Exemple. Chaîne de Markov cachée. La Figure 7.10 montre le modèle graphique dirigé et son graphe moral d’une chaîne de Markov cachée. Rappelons que les \((X_k)_{k\ge 1}\) ne sont pas indépendantes. En revanche, conditionnellement aux \((Z_k)_{k\ge 1}\) les \((X_k)_{k\ge 1}\) sont indépendantes. Concernant la loi aposteriori des variables latentes, on peut écrire \[ \mathbb P(Z_{1},\dots , Z_{n} | X_1 ,\dots , X_n) = \mathbb P (Z_n | Z_{n-1}, \dots, Z_1, X_1,\dots X_n) \mathbb P( Z_{n-1}, \dots, Z_1 | X_1,\dots X_n) . \] D’après le graphe moral, on a \[ \mathbb P (Z_n | Z_{n-1}, \dots, Z_1, X_1,\dots X_n) = \mathbb P ( Z_n | Z_{n-1}, X_n) \] et ainsi \[\begin{equation*} \mathbb P(Z_{1},\dots , Z_{n} | X_1 ,\dots , X_n) = \mathbb P ( Z_n | Z_{n-1}, X_n) \mathbb P( Z_{n-1}, \dots, Z_1 | X_1,\dots X_n) \end{equation*}\] On procède récursivement en utilisant la propriété suivante qui découle du graphe moral \[ \mathbb P (Z_k | Z_{k-1}, \dots, Z_1, X_1,\dots X_n) = \mathbb P ( Z_k | Z_{k-1}, X_k, \dots X_n) \] et on obtient au final \[ \mathbb P(Z_{1},\dots , Z_{n} | X_1 ,\dots , X_n) = \prod_{k=2}^n \mathbb P ( Z_k | Z_{k-1}, X_k,\dots X_n) \times \mathbb P(Z_1 |X_1) . \] Ainsi, la loi des variables latentes sachant les observations est celle d’une chaîne de Markov (inhomogène). La forme factorisée de cette loi la rend aisément manipulable.
En revanche, on voit que les \((Z_i|X_i)_{i\ge 1}\) ne sont pas indépendantes, ce qui pose problème pour l’algorithme EM, car la loi aposteriori n’a pas de forme simple.

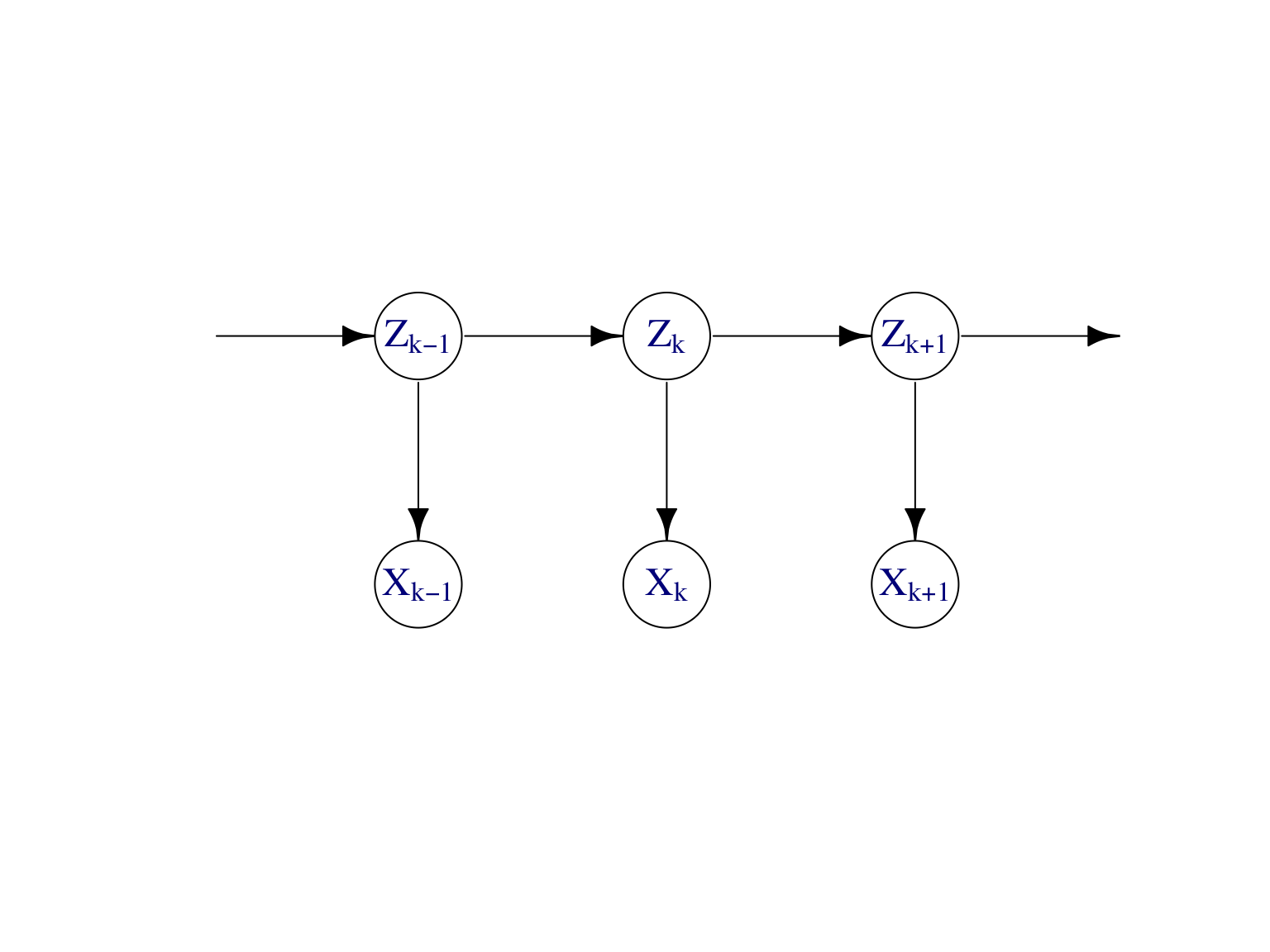
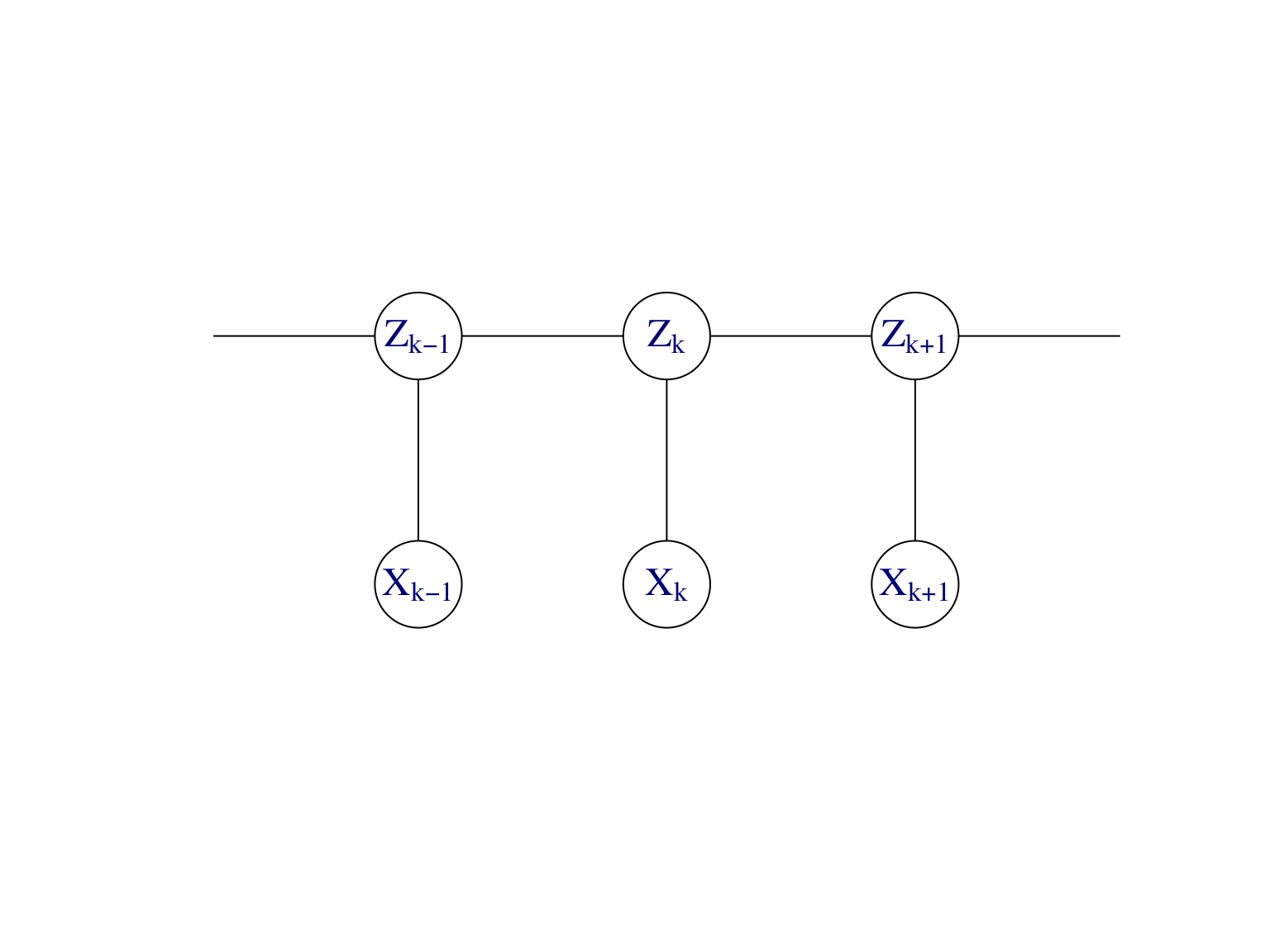
Figure 7.10: Modèle graphique dirigé et son graphe moral d’une chaîne de Markov cachée.

Exercice.

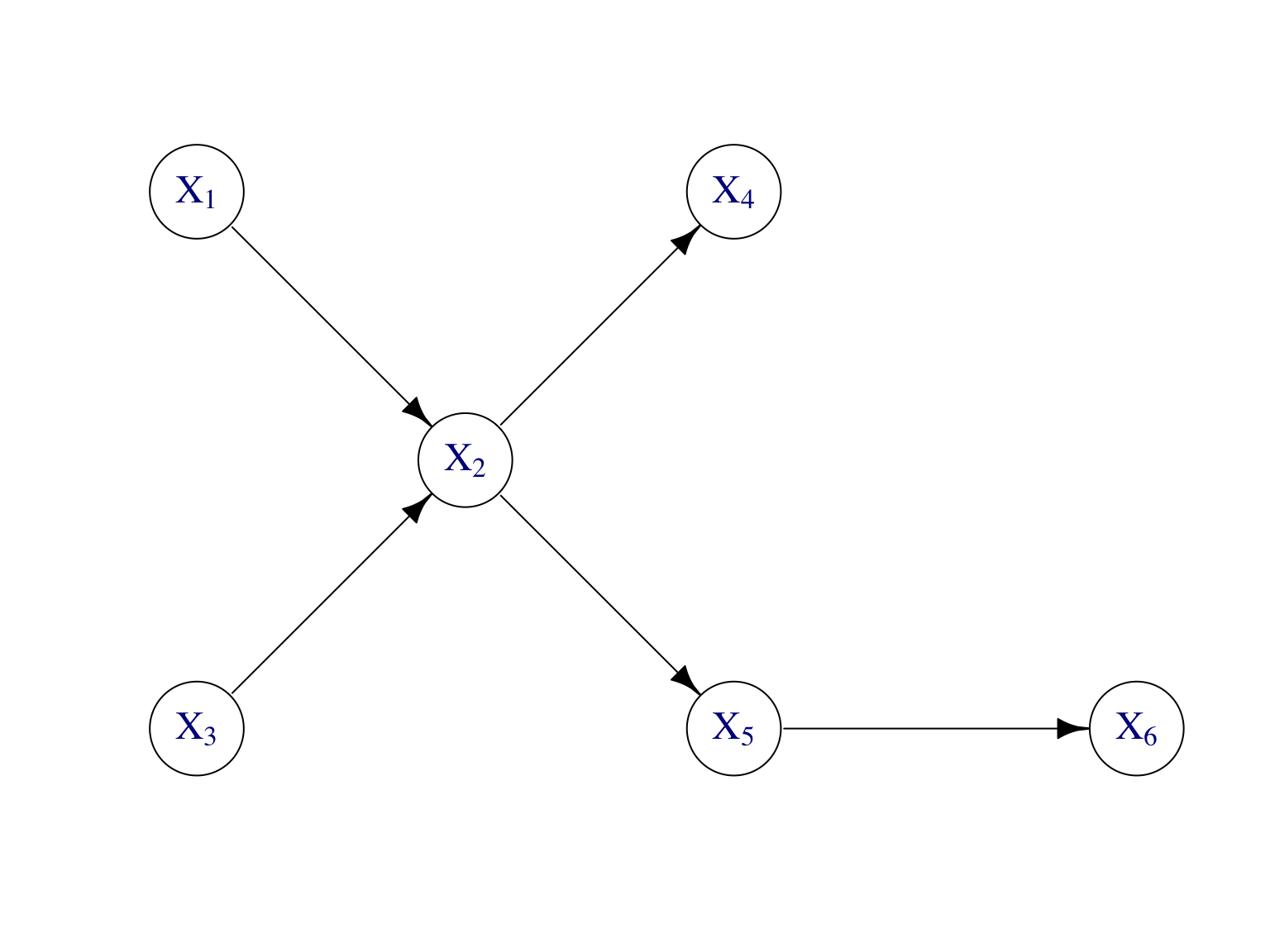
Figure 7.11: Modèle graphique dirigé pour l’exercice.

On considère le modèle graphique dirigé de la Figure 7.11.

1. Construire le graphe moral associé.

2. Quelle la relation entre:

• \(X_1\) et \(X_3\) ?
  
• \(X_1\) et \(X_3\) sachant \(X_2\) ?
  
• la variable \(X_5\) et \((X_1,X_3,X_4)\) sachant \(X_2\) ?
• \(X_2\) et \(X_6\) sachant \(X_5\) ?
• la variable \(X_6\) et \((X_1,X_2,X_3,X_4)\) sachant \(X_5\) ?
• \(X_1\) et \(X_4\) sachant \(X_2\) ?

References

Bishop, Christopher M. 2006. Pattern Recognition and Machine Learning. Information Science and Statistics. Springer, New York.

Lauritzen, Steffen L. 1996. Graphical Models. Vol. 17. Oxford Statistical Science Series. The Clarendon Press, Oxford University Press, New York.