4.2 Algorithmes de spectral clustering

4.2.1 Heuristique

Nous avons vu que le spectre des différents laplaciens porte de l’information sur le nobmre de composantes connexes d’un graphe. Or, en pratique, il est facile de déterminer les composantes connexes, sans avoir recours à l’analyse spectrale d’un laplacien.

L’heuristique du spectral clustering repose sur la propriété suivante: si une matrice \(M\) est perturbée légèrement, p.ex. en additionnant un bruit \(B\), alors le spectre de la matrice \(\tilde M=M+B\) est proche de celui de \(M\). Or, un graphe \(G\) structuré en quasi-cliques, disons de nombre \(k\), peut être considéré comme la perturbation d’un graphe avec \(k\) vraies cliques, i.e. \(k\) composantes connexes, auquel on a ajouté quelques arêtes. Et donc on s’attend à ce que le spectre de \(G\) soit proche du spectre d’un graphe à \(k\) composantes connexes. En particulier, on s’attend à la présence de \(k\) valeurs propres très proches de 0, et les vecteurs propres associés contiennent de l’information sur les clusters.

Cette heuristique peut être formalisée et par la théorie de perturbation de matrice on peut donner une justification rigoureuse à l’approche du spectral clustering.

On utilise alors le spectre du laplacien de la façon suivante: Pour le laplacien normalisé \(L_N\) par exemple, on s’intéresse aux \(k\) premiers vecteurs propres, ce qui est similaire à une ACP (analyse en composantes principales) ou du MDS (multi-dimensional scaling). Dans ce nouvel espace, les valeurs associées aux noeuds du graphe sont mieux séparées et un simple clustering (type \(k\)-means) dans ce nouvel espace permet de trouver les clusters.

4.2.2 Rappel: \(k\)-means

Raappelon d’abord l’algorithme de \(k\)-means qui est utiliser dans le spectral clustering pour partionner les nouveaux points obtenus par projection spectrale.

Le \(k\)-means est la méthode de clustering la plus populaire pour partitionner des observations en des groupes homogènes. Soient \(x_1,\dots,x_n\in \mathbb R^p\) des points à grouper en \(k\) clusters. Idéalement, on cherche une partition \((C_1^\star,\dots,C_k^\star)\) de \(\{1,\dots,n\}\) qui minimise \[\begin{equation} (C_1,\dots,C_k)\mapsto\sum_{\ell=}^k\sum_{x_i\in C_\ell}\|x_i-\mu_\ell\|^2, \tag{4.2} \end{equation}\] où \(C_1,\dots,C_k\) est un partitionnement de \(\{1,\dots,n\}\) et \(\mu_\ell=\frac1{|C_\ell|}\sum_{x_i\in C_\ell}x_i\) est le barycentre du \(\ell\)-ième cluster.

L’algorithme k-means cherche à approcher la solution par une procédure itérative, en alternant la maximisation du critère en (4.2) par rapport à \((C_1,\dots,C_k)\) et aux barycentres \((\mu_1, \dots,\mu_k)\).

Algorithme. \(k\)-means

Entrée: observations \(x_1,\dots,x_n\in \mathbb R^p\), nombre \(k\) de clusters.

Sortie: Clusters de noeuds \(C_1,\dots,C_k\) qui partitionnent \(\{1,\dots,n\}\).

Procédure:

  • Initialiser avec \(k\) points \(\mu_1,\dots,\mu_k\) (p. ex. choisis au hasard)

  • Répéter jusqu’à convergence:

    • assigner chaque observation \(x_i\) au point \(\mu_i\) le plus proche: \[C_\ell=\left\{x_i:\|x_i-\mu_\ell\|^2 < \|x_i-\mu_j\|^2~ \forall j\neq \ell\right\}.\]
    • mettre à jour les barycentres: \[\mu_\ell=\frac1{|C_\ell|}\sum_{x_i\in C_\ell}x_i.\]

4.2.3 Trois algorithmes

Tout comme il existe plusieurs définitions de la matrice laplacienne d’un graphe, il existe plusieurs algorithmes de clustering spectral. Nous en présentons trois ici: le spectral clustering basé sur le laplacien non normalisé \(L\), l’algorithme de spectral clustering normalisé qui utilise \(L_{N}\) (Ng, Jordan, and Weiss 2001) et le spectral clustering fondé sur \(L_{\text{abs}}\) (Rohe, Chatterjee, and Yu 2011).

Algorithme. Spectral clustering avec le laplacien non normalisé \(L\)

Entrée: \(A\) de taille \(n\times n\) d’entrées positives, nombre \(k\) de clusters

Sortie: Clusters \(C_1,\dots,C_k\) qui partitionnent \(\{1,\dots,n\}\)

Procédure:

  • Calculer la matrice laplacienne non normalisée \(L\)

  • Calculer les \(k\) vecteurs propres \(u_1,\dots, u_k\) associés aux plus petites valeurs propres de \(L\)

  • Former la matrice \(U\) de taille \(n\times k\) dont les colonnes sont \(u_1,\dots, u_k\)

  • Créer des clusters \(C_1,\dots,C_k\) sur les \(n\) lignes de \(U\) par \(k\)-means

Algorithme. Spectral clustering normalisé de Ng, Jordan, and Weiss (2001)

Entrée: \(A\) de taille \(n\times n\) d’entrées positives, nombre \(k\) de clusters

Sortie: Clusters \(C_1,\dots,C_k\) qui partitionnent \(\{1,\dots,n\}\)

Procédure:

  • Calculer la matrice laplacienne normalisée \(L_{N}\)

  • Calculer les \(k\) vecteurs propres \(u_1,\dots, u_k\) associés aux plus petites valeurs propres de \(L_N\).

  • Former la matrice \(U\) de taille \(n\times k\) dont les colonnes sont \(u_1,\dots, u_k\)

  • Former la matrice \(T\) de taille \(n\times k\) en normalisant les lignes de \(U\) pour avoir une norme euclidienne 1 (i.e. \(t_{ij}= u_{ij}/\sqrt{\sum_k u_{ik}^2}\))

  • Créer des clusters \(C_1,\dots,C_k\) sur les \(n\) lignes de \(T\) par \(k\)-means

Algorithme. Spectral clustering de Rohe, Chatterjee, and Yu (2011)

Entrée: \(A\) de taille \(n\times n\) d’entrées positives, nombre \(k\) de clusters

Sortie: Clusters \(C_1,\dots,C_k\) qui partitionnent \(\{1,\dots,n\}\)

Procédure:

  • Calculer la matrice laplacienne \(L_{\text{abs}}\)

  • Calculer les \(k\) vecteurs propres \(u_1,\dots, u_k\) de \(L_{\text{abs}}\) associés aux \(k\) plus grandes valeurs propres en valeur absolue

  • Former la matrice \(U\) de taille \(n\times k\) dont les colonnes sont \(u_1,\dots, u_k\)

  • Créer des clusters \(C_1,\dots,C_k\) sur les \(n\) lignes de \(U\) par \(k\)-means.

Le principe du spectral clustering est donc de transformer les observations de départ \(x_i \in \mathbb R^p, 1\le i \le n\) en un nouvel ensemble de points \(y_i\in \mathbb R^k, 1\le i \le n\) (=les lignes de la matrice \(U\)), via un graphe de similarité, la matrice laplacienne associée et ses \(k\) premiers vecteurs propres. Les propriétés de ces matrices laplaciennes font que ce nouvel ensemble de points \(y_i\) est facilement classifiable en \(k\) groupes (un simple algorithme \(k\)-means suffit à bien séparer ces nouveaux points).

Si le graphe de départ a \(k\) composantes connexes, les \(k\) premiers vecteurs propres \(u_1,\dots, u_k\) engendrent l’espace propre associé à la valeur propre 0, et on a vu que cet espace est engendré par les vecteurs indicatrices \(\mathbb 1_{C_1},\dots , \mathbb 1_{C_k}\). Cependant, la sortie d’un algorithme de décomposition spectrale est n’importe quelle base orthogonale de vecteurs propres de cet espace (i.e. pas forcément la base des vecteurs d’indicatrices mais une base issue d’une combinaison linéaire de celle-ci). Cependant, si on applique l’algorithme des \(k\)-means sur les lignes de \(U\) avec \(k\) groupes, on retrouve exactement les composantes connexes \(C_1,\dots, C_k\). En fait, la matrice \(U\) n’a que \(k\) lignes différentes, on peut faire le clustering visuellement.

Par analogie, lorsqu’on a une seule composante connexe, les algorithmes de spectral clustering vont donner un partitionnement des noeuds du graphe en un ensemble de ‘presque composantes connexes’ ou plus exactement, de communautés.

Particularité de l’algorithme de Rohe, Chatterjee, and Yu (2011)

Le spectral clustering de Rohe, Chatterjee, and Yu (2011) a une propriété supplémentaire: en plus des communautés, l’algorithme cherche des structures de type biparties dans le graphe. Il tend à mettre dans le même groupe des noeuds qui partagent beaucoup de voisins.

Calucl de vecteurs propres

L’algorithme de spectral clustering nécessiste le calcul de vecteurs propres, ce qui peut poser un problème numérique notamment quand le graphe est très grand. Il existe des algorithmes très efficaces pour approcher les premiers vecteurs propres dans le cas de matrices creuses, i.e. des matrices dont la plupart d’entrées sont nulles (voir Luxburg (2007) pour plus de détails).

Notons que si la densité d’un graphe est très faible, ce qui est le cas de beaucoup de graphes observés en pratique, la matrice d’adjacence et ainsi le laplacien sont des matrices creuses et donc ces algorithmes peuvent être appliquées.

4.2.4 Choix du nombre de clusters

Le choix du nombre de clusters \(k\) est un problème récurrent du clustering. Comme il n’y a pas de modèle probabiliste ici, il n’y a pas de critère type BIC ou un autre critère reposant sur une vraisemblance. En revanche, on peut utiliser d’autres critères ad-hoc type similarité intra-groupes et inter-groupes.

Une technique courante pour le spectral clustering avec le laplaciens \(L\) et \(L_N\) consiste à utiliser l’heuristique du trou des valeurs propres ou eigengap: on choisit le nombre de clusters \(k\) par \[ \hat k =\arg\max_{1\le j \le n-1} \lambda_{j+1}-\lambda_j, \] où \(\lambda_j\) désignent les valeurs propres du laplacien.

Pour le laplacien \(L_{\text{abs}}\) il n’y a pas de règle équivalente.

4.2.5 Exemples jouets

On considère ici le cas de quelques graphes remarquables: on étudie leur spectre (avec \(L\) au lieu de \(L_N\) ou de \(L_{\text{abs}}\) car les calculs sont plus simples) et on essaye de voir l’impact sur le principe du clustering.

Proposition 4.3 Soit \(K_n\) le graphe complet sur \(n\) noeuds, alors les valeurs propres du laplacien non normalisé \(L\) associé sont: 0 de multiplicité 1 et \(n\) de multiplicité \(n-1\).
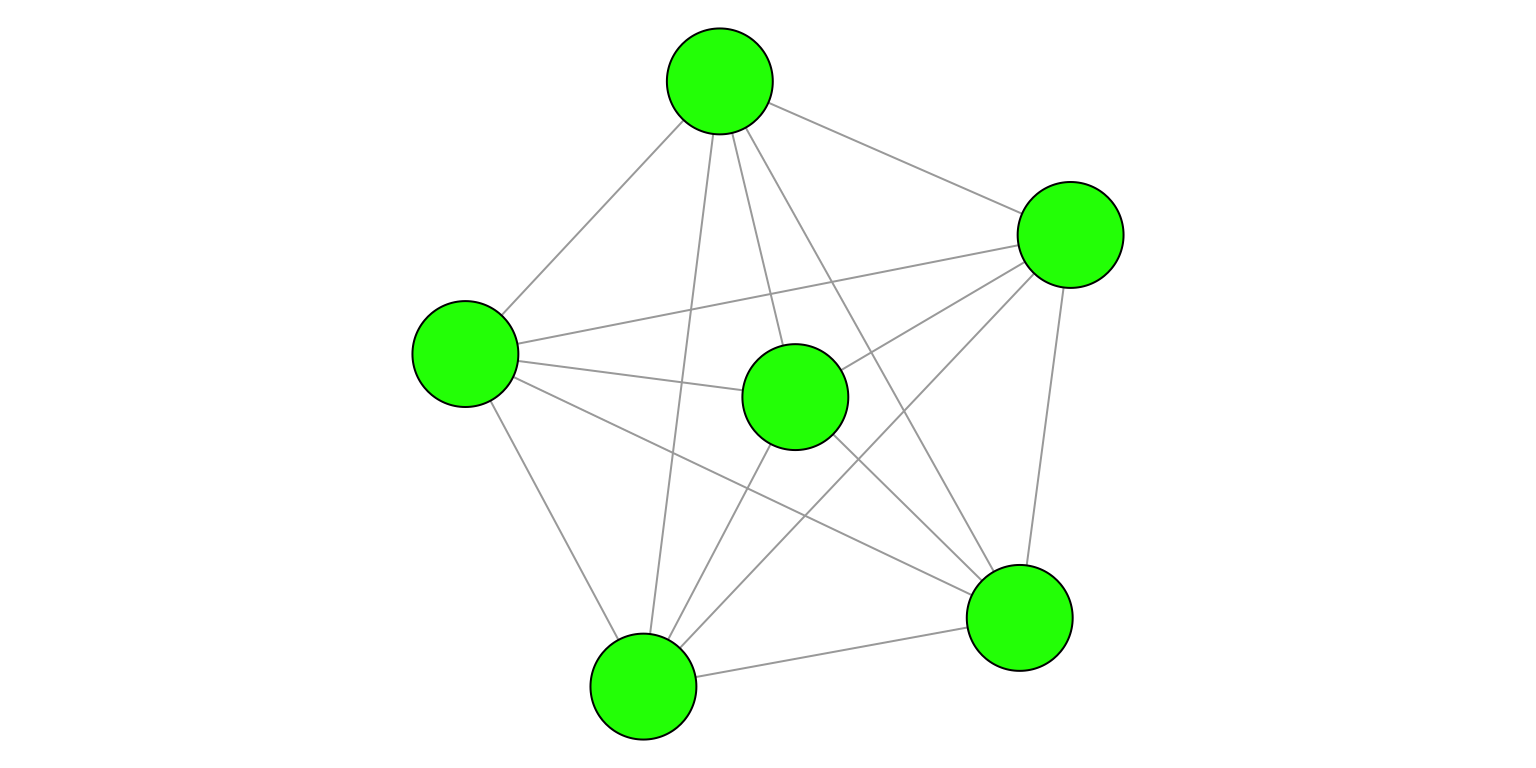
Graphe complet $K_n$.

Figure 4.2: Graphe complet \(K_n\).

Proof. \(K_n\) est connexe donc \(0\) est valeur propre de multiplicité 1, associée au vecteur propre \(\mathbb 1\). Soit \(u\in \mathbb R^n\) un vecteur propre associé à une valeur propre \(\lambda >0\), alors \(u\) est orthogonal à \(\mathbb 1\), i.e. \(\sum_{i=1}^n u_i=0\). Sans perte de généralité, on peut supposer \(u_1\neq 0\) et on a \(u_1 = -\sum_{i=2}^n u_i \neq 0\). De plus, le laplacien \(L\) de \(K_n\) vérifie \(L_{ij}=-1\) si \(i\neq j\) et \(L_{ii}=n-1\). On obtient alors \[\begin{align*} (Lu)_1 = \sum_{i=1}^n L_{1i} u_i = (n-1) u_{1} -\sum_{i=2}^n u_{i} = n u_1 . \end{align*}\] Donc si \(u\) est un vecteur propre pour la valeur propre \(\lambda\), on a \(\lambda u_1 = (Lu)_1=n u_1\). Donc \(n\) est la seule autre valeur propre (elle a la multiplicité \(n-1\) et est associé à n’importe quel vecteur orthogonal à \(\mathbb 1\)).
Proposition 4.4 Soient \(i,j\) deux noeuds de degré 1 qui partagent le même voisin \(k\) dans le graphe \(G\). Alors le vecteur \(u\in \mathbb R^n\) défini par \(u_i=1,u_j=-1\) et \(u_l=0\) pour tout \(l\in \{1,\dots,n\}\setminus\{i,j\}\) est un vecteur propre du laplacien non normalisé \(L\) associé à la valeur propre 1.
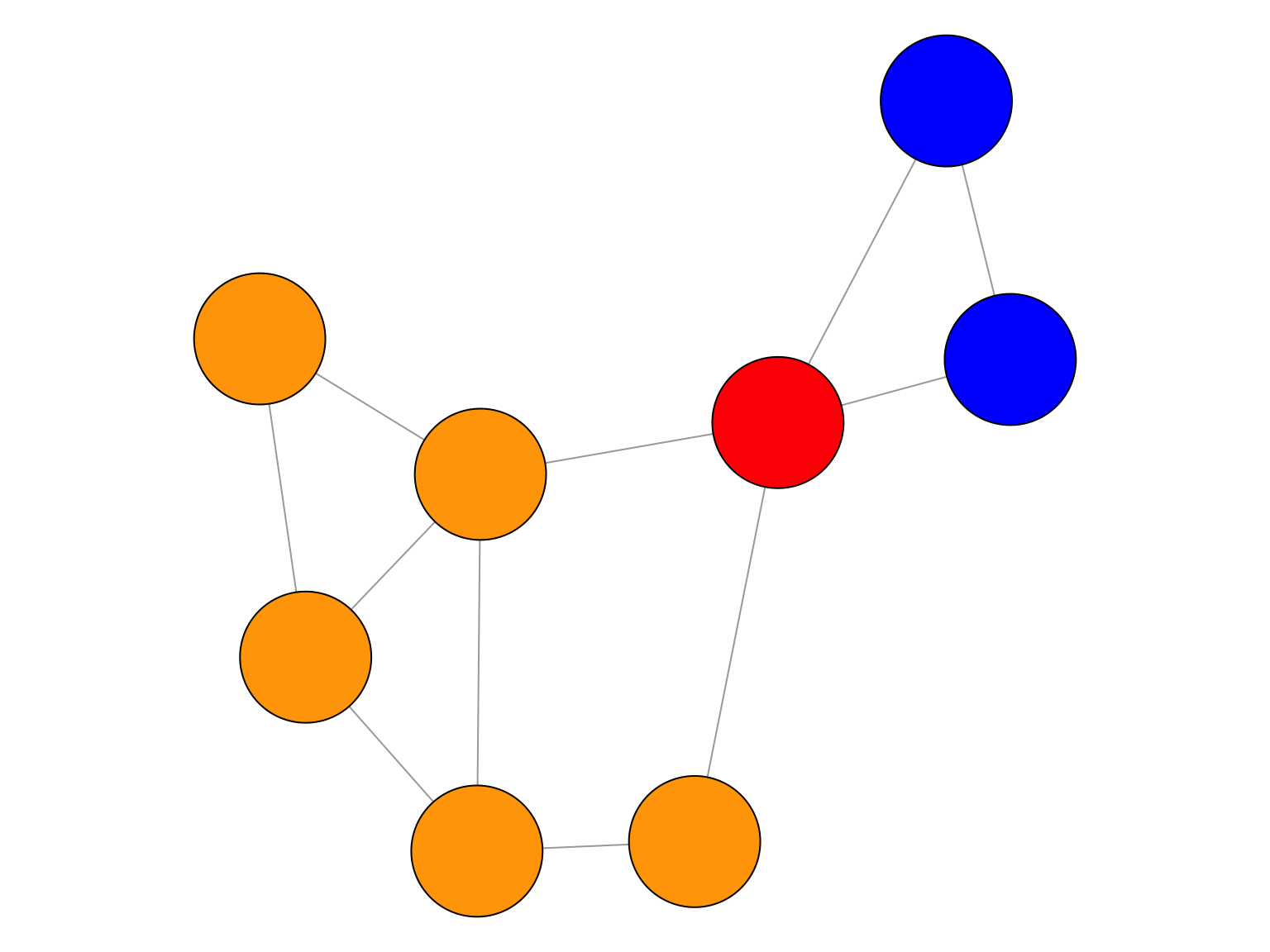
Graphe complet $K_n$.

Figure 4.3: Graphe complet \(K_n\).

Proof. Quitte à réordonner les noeuds du graphe, on peut écrire le laplacien sous la forme \[ L= \begin{pmatrix} 1 & 0 & -1 & 0 \dots 0\\ 0 & 1 & -1 & 0 \dots 0\\ -1 &- 1 & d_k & \star \star\star \\ 0 & 0 & \star & \\ \vdots & \vdots & \star & \star \star \\ 0 & 0 & \star & \end{pmatrix} . \] Alors, le vecteur \(u^\intercal = (1, -1, 0, \dots, 0)\) est un vecteur propre associé à la valeur propre 1.
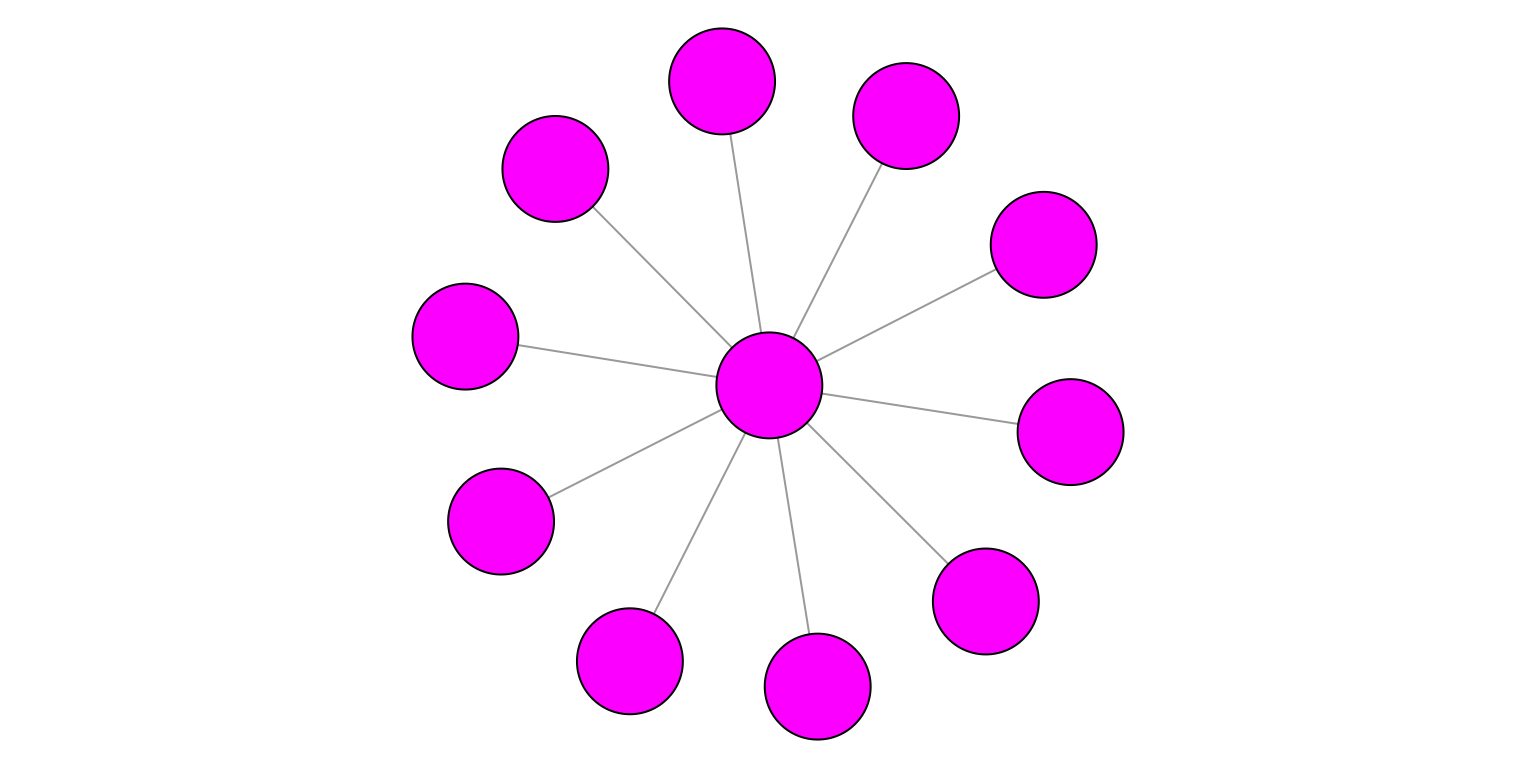
Proposition 4.5 Soit \(S_n\) le graphe en étoile sur \(n\) noeuds, alors les valeurs propres du laplacien non normalisé \(L\) associé sont: 0 de multiplicité 1, 1 de multiplicité \(n-2\) et \(n\) de multiplicité \(1\).
Graphe en étoile.

Figure 4.4: Graphe en étoile.

Proof. On considère à présent le graphe en étoile \(S_n\). Il est connexe donc \(0\) est valeur propre de multiplicité 1, associée au vecteur propre \(\mathbb 1\). On numérote 1 le noeud au centre de l’étoile et de \(2\) à \(n\) les noeuds au bout des branches. En appliquant le résultat du point 2 pour les noeuds \((i,i+1)\) pour \(i\) allant de \(2\) à \(n-1\) (ce sont des noeuds de degré 1 qui partagent le noeud 1 en commun), on obtient (n-2) vecteurs \(u^{(i)}\) associés à la valeur propre 1. On vérifie qu’ils sont linéairement indépendants (écrire \(\sum_{i=2}^{n-1}\alpha_i u^{(i)}=0\) et voir que nécessairement \(\alpha_i=0\)). Enfin pour trouver la dernière valeur propre \(\lambda\), on utilise \(Tr(L)=\sum_{i=1}^n \lambda_i= \lambda + 0 + (n-2)\). Or \(Tr(L)= (n-1)+ 1\times (n-1)=2n -2\), donc \(\lambda = Tr(L)-n+2=n\). (Le vecteur propre correspondant est nécessairement constant sur les indices \(i\) allant de 2 à \(n\) et orthogonal à \(\mathbb 1\), on peut déduire facilement sa forme).


Remarques.

  • Le résultat pour une clique \(K_n\) indique que si on fait un clustering des lignes de \(U\) avec \(k>1\) groupes, on n’obtient rien qui fasse du sens. C’est normal puisqu’il n’y a qu’une seule communauté dans \(K_n\).

  • Pour l’étoile \(S_n\), le clustering spectral trouve soit une seule communauté, soit \(n-1\) communautés: le noeud central associé à un noeud au hasard, puis chaque autre noeud tout seul.

References

Luxburg, Ulrike von. 2007. “A Tutorial on Spectral Clustering.” Statistics and Computing 17 (4): 395–416. http://dx.doi.org/10.1007/s11222-007-9033-z.

Ng, Andrew Y., Michael I. Jordan, and Yair Weiss. 2001. “On Spectral Clustering: Analysis and an Algorithm.” In Advances in Neural Information Processing Systems, 849–56. MIT Press.

Rohe, K., S. Chatterjee, and B. Yu. 2011. “Spectral Clustering and the High-Dimensional Stochastic Blockmodel.” Annals of Statistics 39 (4): 1878–1915.