2.8 TP – Exploration des données | Analyse statistique de graphes

2.8 TP – Exploration des données

Les données utilisées dans ce TP sont disponibles sur en ligne.

Dans ce TP nous allons découvrir les fonctions du package igraph pour calculer différentes statisitiques de graphe. Chargons alors la library igraph:

library(igraph)

ainsi que deux jeux de données que nous avons déjà vu au dernier TP:

miserab <- read_graph(file='lesmis.gml', format="gml")

friends <- read.table(file='Friendship-network_data_2013.csv')
amis <- graph_from_data_frame(friends, directed=TRUE)

Propiétés de base d’un graphe

Rappelons les fonctions suivantes pour déterminer l’ordre et la taille d’un graphe, obtenir la liste des noeuds ou d’arêtes ainsi que savoir si le graphe est orienté ou non:

vcount(miserab)

## [1] 77

ecount(miserab)

## [1] 254

V(miserab)

## + 77/77 vertices, from 35f79c9:
##  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
## [26] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
## [51] 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75
## [76] 76 77

E(miserab)

## + 254/254 edges from 35f79c9:
##   [1]  1-- 2  1-- 3  1-- 4  3-- 4  1-- 5  1-- 6  1-- 7  1-- 8  1-- 9  1--10
##  [11] 11--12  4--12  3--12  1--12 12--13 12--14 12--15 12--16 17--18 17--19
##  [21] 18--19 17--20 18--20 19--20 17--21 18--21 19--21 20--21 17--22 18--22
##  [31] 19--22 20--22 21--22 17--23 18--23 19--23 20--23 21--23 22--23 17--24
##  [41] 18--24 19--24 20--24 21--24 22--24 23--24 13--24 12--24 24--25 12--25
##  [51] 25--26 24--26 12--26 25--27 12--27 17--27 26--27 12--28 24--28 26--28
##  [61] 25--28 27--28 12--29 28--29 24--30 28--30 12--30 24--31 31--32 12--32
##  [71] 24--32 28--32 12--33 12--34 28--34 12--35 30--35 12--36 35--36 30--36
##  [81] 35--37 36--37 12--37 30--37 35--38 36--38 37--38 12--38 30--38 35--39
##  [91] 36--39 37--39 38--39 12--39 30--39 26--40 26--41 25--42 26--42 42--43
## + ... omitted several edges

is.directed(miserab)

## [1] FALSE

et pour le graphe d’amis:

vcount(amis)

## [1] 134

ecount(amis)

## [1] 668

V(amis)

## + 134/134 vertices, named, from f65e8a1:
##   [1] 1    3    27   28   32   34   45   46   48   55   61   63   70   72   79  
##  [16] 80   85   92   101  117  119  120  122  124  125  132  134  147  151  156 
##  [31] 159  165  170  173  184  190  196  200  201  202  205  211  213  214  219 
##  [46] 222  232  240  242  245  248  252  255  257  265  268  272  275  277  285 
##  [61] 312  325  327  335  343  353  364  366  388  407  425  429  440  441  447 
##  [76] 452  465  468  471  480  486  488  491  492  494  496  498  502  520  531 
##  [91] 545  564  576  577  587  601  603  605  612  622  624  634  642  674  691 
## [106] 694  753  765  769  771  779  797  798  845  857  866  867  869  883  884 
## [121] 894  920  959  960  970  974  1228 1332 1401 1485 1519 1594 1828 38

E(amis)

## + 668/668 edges from f65e8a1 (vertex names):
##  [1] 1 ->55  1 ->205 1 ->272 1 ->494 1 ->779 1 ->894 3 ->1   3 ->28  3 ->147
## [10] 3 ->272 3 ->407 3 ->674 3 ->884 27->63  27->173 28->202 28->327 28->353
## [19] 28->407 28->429 28->441 28->492 28->545 32->440 32->624 32->797 32->920
## [28] 34->151 34->277 34->502 34->866 45->48  45->79  45->335 45->496 45->601
## [37] 45->674 45->765 46->117 46->196 46->257 46->268 48->45  48->79  48->496
## [46] 55->1   55->170 55->205 55->252 55->272 55->779 55->883 55->894 61->797
## [55] 63->27  63->125 63->173 70->101 70->132 70->240 70->425 70->447 72->407
## [64] 72->674 72->857 79->45  79->48  79->335 79->496 79->601 79->674 79->765
## [73] 80->120 80->285 80->468 80->601 85->190 85->213 85->214 85->335 85->603
## [82] 85->605 85->765 92->468 92->845
## + ... omitted several edges

is.directed(amis)

## [1] TRUE

Les degrés avec `igraph`

Dans le cas d’un graphe non dirigé, calcul des degrés:

degree(miserab)

##  [1] 10  1  3  3  1  1  1  1  1  1  1 36  2  1  1  1  9  7  7  7  7  7  7 15 11
## [26] 16 11 17  4  8  2  4  1  2  6  6  6  6  6  3  1 11  3  3  2  1  1  2 22  7
## [51]  2  7  2  1  4 19  2 11 15 11  9 11 13 12 13 12 10  1 10 10 10  9  3  2  2
## [76]  7  7

Dans le cas d’un graphe dirigé, calcul des degrés entrants et sortants:

degree(amis, mode="out")

##    1    3   27   28   32   34   45   46   48   55   61   63   70   72   79   80 
##    6    7    2    8    4    4    7    4    3    8    1    3    5    3    7    4 
##   85   92  101  117  119  120  122  124  125  132  134  147  151  156  159  165 
##    7    2    9   16    6    3    5    2    9    7    3   10   13    1    2    1 
##  170  173  184  190  196  200  201  202  205  211  213  214  219  222  232  240 
##    6    3    3    4    5    2    8    5   12    3    2    3    1    3    2    7 
##  242  245  248  252  255  257  265  268  272  275  277  285  312  325  327  335 
##    3    7    3    7    1    3    9    5   11    3    6    5    2    7    8    3 
##  343  353  364  366  388  407  425  429  440  441  447  452  465  468  471  480 
##    3    5    5    1    8   13   10    7    5    7    8    5    3    7    2    2 
##  486  488  491  492  494  496  498  502  520  531  545  564  576  577  587  601 
##    2    3    4    9    8    8    2    5    4    3    3    2    4    2    5    7 
##  603  605  612  622  624  634  642  674  691  694  753  765  769  771  779  797 
##    6    5    2    8   10    3    7    6   10    2    2    3    9    2    9    5 
##  798  845  857  866  867  869  883  884  894  920  959  960  970  974 1228 1332 
##    2    6    5    9    2    4   13    2   11    3    6    2    2    2    3    6 
## 1401 1485 1519 1594 1828   38 
##    4    1    6    2    2    0

degree(amis, mode="in")

##    1    3   27   28   32   34   45   46   48   55   61   63   70   72   79   80 
##   11    4    3   10    2    4    8    5    5    9    0    2    5    4    8    5 
##   85   92  101  117  119  120  122  124  125  132  134  147  151  156  159  165 
##    5    3    8   11    8    4    6    2    7    6    4    3    5    0    0    1 
##  170  173  184  190  196  200  201  202  205  211  213  214  219  222  232  240 
##    8    2    5    4    6    4    4    3   11    3    3    5    4    3    2    6 
##  242  245  248  252  255  257  265  268  272  275  277  285  312  325  327  335 
##    3    9    2    7    2    4    7    5   15    3    3    4    2    6    6    6 
##  343  353  364  366  388  407  425  429  440  441  447  452  465  468  471  480 
##    4    6    6    1    5   12    8    5    3    8    9    8    4    6    2    2 
##  486  488  491  492  494  496  498  502  520  531  545  564  576  577  587  601 
##    2    3    4    6    8    7    2    6    3    3    3    3    3    2    7    4 
##  603  605  612  622  624  634  642  674  691  694  753  765  769  771  779  797 
##    5    7    2    7    7    9    8    6   13    5    4    6    4    1    9   10 
##  798  845  857  866  867  869  883  884  894  920  959  960  970  974 1228 1332 
##    4    5    3    5    2   10   12    3    9    2    5    5    2    2    2    7 
## 1401 1485 1519 1594 1828   38 
##    4    1    5    2    2    3

Distribution empirique des degrés:

degree_distribution(miserab)

##  [1] 0.00000000 0.22077922 0.12987013 0.07792208 0.03896104 0.00000000
##  [7] 0.06493506 0.12987013 0.01298701 0.03896104 0.06493506 0.07792208
## [13] 0.02597403 0.02597403 0.00000000 0.02597403 0.01298701 0.01298701
## [19] 0.00000000 0.01298701 0.00000000 0.00000000 0.01298701 0.00000000
## [25] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
## [31] 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000
## [37] 0.01298701

degree_distribution(amis, mode="out")

##  [1] 0.007462687 0.052238806 0.194029851 0.179104478 0.074626866 0.111940299
##  [7] 0.074626866 0.104477612 0.067164179 0.052238806 0.029850746 0.014925373
## [13] 0.007462687 0.022388060 0.000000000 0.000000000 0.007462687

Représentation graphique de la distribution empirique des degrés:

barplot(degree_distribution(miserab), names.arg=as.character(0:max(degree(miserab))), col='green', main='Degrés des noeuds des Misérables')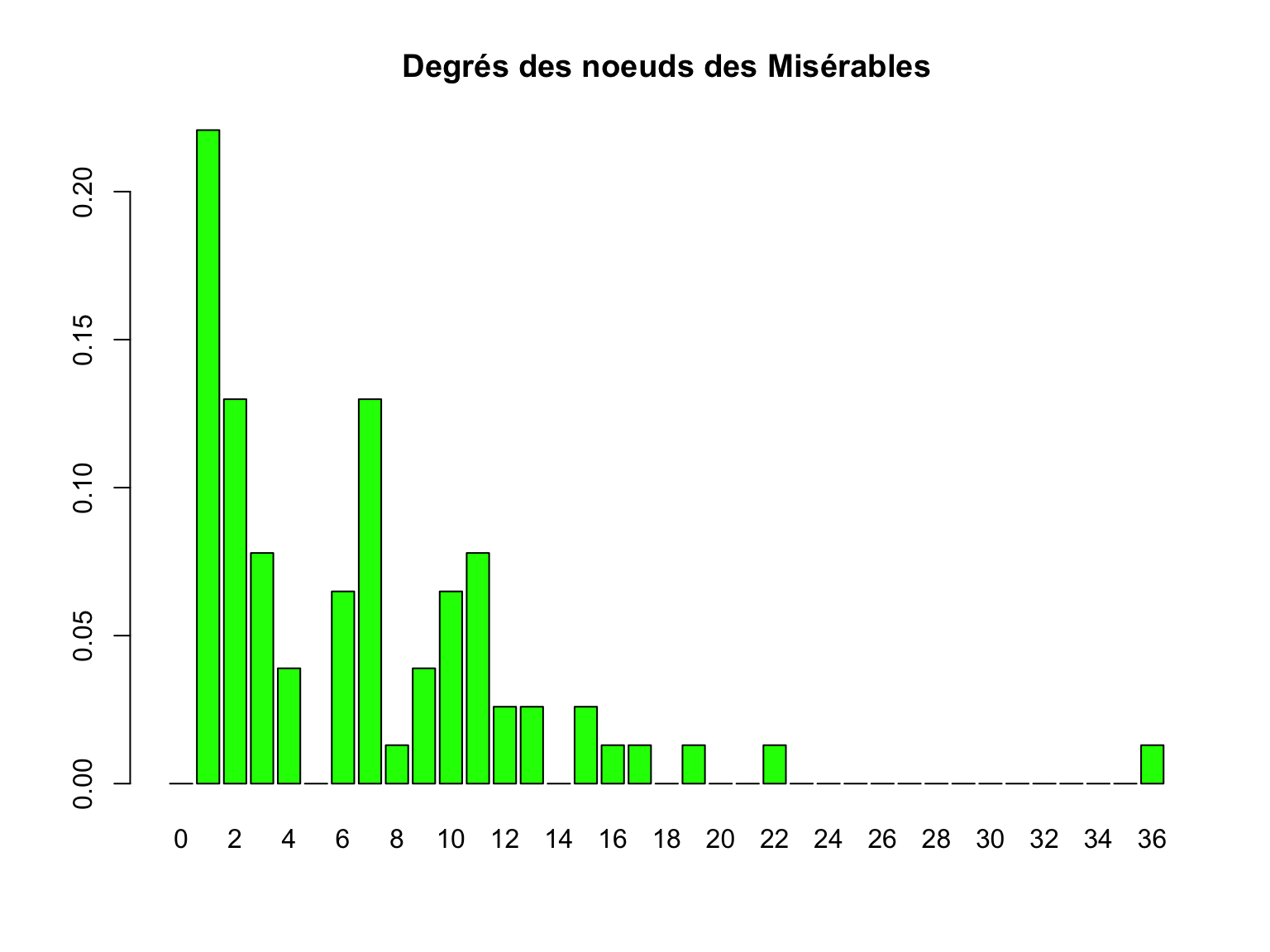

Les degrés par la matrice d’adjacence On peut vérifier à la main que les degrés des noeuds sont bien donnés par la somme de la ligne ou de la colonne de la matrice d’adjacence:

Aamis <- as_adj(amis)
sum(Aamis[1,])

## [1] 6

degree(amis, mode="out")[1]

## 1 
## 6

sum(Aamis[,1])

## [1] 11

degree(amis, mode="in")[1]

##  1 
## 11

Autres indicateurs

Familiarisez-vous avec les fonctions suivantes d’igraph pour un graphe G, et appliquez-les aux graphes des misérables et d’amis:

components(G)                      
edge_density(G)
diameter(G, directed=TRUE, unconnected=FALSE)
diameter(G, directed=TRUE, unconnected=TRUE)
get_diameter(G, directed=TRUE)
count_triangles(G) 
transitivity(G)

neighbors(G, 1, mode='out')
neighbors(G, 1, mode='in')
neighbors(G, 1, mode='all')
 
K3 <- cliques(G, min=3, max=3)
K3[[1]] 
length(K3) 

closeness(G) 
betweenness(G)
plot(G, vertex.size=betweenness(G))

Exercice 2.

Analysez les graphes de l’exercice 1 Chapitre ??.
In 1977, W. W. Zachary recorded interactions in a karate club for two years. During observation, a conflict developed between the administrator and the instructor.

library(igraphdata)
data(karate)