2.6 Clustering, transitivité
Le clustering est la propriété que le graphe est composé de groupes de sommets très connectés entre eux. Le réseau est alors organisé en cliques ou quasi-cliques. Une clique est un sous-graphe complet, c’est-à-dire chaque noeud est connecté à tous les autres.
Dans les réseaux sociaux avec une grande cohésion sociale on observe le principe Les amis de mes amis sont mes amis. Pour quantifier le clustering, on peut alors mesurer à quel point les voisins d’un noeud \(i\) sont connectés entre eux.
Les coefficients définis dans cette section analysent l’environnement local d’un noeud en incluant les interactions de leurs voisins entre eux.
Introduisons d’abord quelques notations pour un graphe non-dirigé \(G=(V,E)\).
- On note \(\lambda_i\) le nombre de triangles dont le noeud \(i\in V\) fait partie, et \(\lambda(G)=\frac13\sum_{i=1}^n\lambda_i\) le nombre de triangles dans le graphe \(G\) entier.
- Notons \(\tilde G_{i}=(\mathcal{V}(i)\cup\{i\}, \tilde E_i)\) le sous-graphe induit de \(G\) constitué du noeud \(i\) et de ses voisins \(\mathcal{V}(i)=\{j \in V ; \{i,j\}\in E\}\).
- Un triplet est un ensemble de 3 noeuds tels que le sous-graphe induit par ces 3 noeuds est connexe.
- On note \(\tau_i\) le nombre de triplets contenant le noeud \(i\) dans \(\tilde G_i\), et \(\tau(G)= \sum_{i=1}^n\tau_i\). On peut exprimer le nombre de triplets \(\tau_i\) du noeud \(i\) en termes de degré du noeud. On a \[ \tau_i = \frac{d_i(d_i-1)}2. \]
Definition 2.8 Soit \(G=(V,E)\) un graphe non-dirigé.
- On définit le coefficient \(C_i\) de clustering du noeud \(i\) par \[ C_i = \left\{ \begin{array}{ll} \frac{\lambda_i}{\tau_i} & \text{ si } d_i\ge 2\\ 0 & \text{ sinon } \end{array} \right. \]
- Notons \(V'=\{i\in V: D_i\geq2\}\) le sous-ensemble de noeuds tels que \(C_i>0\). Le coefficient \(C(G)\) de clustering global est défini par \[ C(G) = \frac 1{|V'|}\sum_{i\in V'}C_i. \]
En fait, le coefficient \(C_i\) de clustering du noeud \(i\) correspond à la densité du sous-graphe \(\bar G_i=(\mathcal V(i), \bar E_i)\) induit par les voisins de \(i\) (mais sans le noeud \(i\)). Si ^\(d_i>1\), on a \[ C_i = \text{dens}(\bar G_i)=\frac{2 |E_i|}{d_i(d_i-1)}. \]
On peut interpréter \(C_i\) comme la densité de triangles dans le sous-graphe induit par les voisins de \(i\). Si toutes les arêtes possibles entre ces voisins existent, i.e. si tous les triplets sont des triangles, alors \(C(G)=1\). Mais cela n’implique pas qu’il s’agit d’un graphe complet.
Si le graphe ne contient aucun triangle, alors \(C(G)=0\). Mais il peut toujours contenir des cycles de longueur supérieure ou égale à 4. Des réseaux de métro par exemple ne contienne quasi pas de triangles et ont donc un coefficient de clustering proche de 0, cf. Figure 1.4.
En général, on a
\[
0\le C(G) \le 1.
\]
Le coefficient de clustering global est relié à la densité des triangles parmi les paires de relations dans le graphe. Les triangles traduisent les relations de transitivité: importance par exemple dans les réseaux sociaux, etc. On peut aussi mesurer directement cette densité des triangles par le coefficient de transitivité.
Pour un arbre, on a \(C(G)=0=T(G)\), mais ce n’est pas un condition suffisante. Un graphe avec des cycles peut également avoir des petites valeurs de \(T(G)\) et de \(C(G)\).
Exercice.
- Déterminer le coefficient de clustering \(C_i\) de chaque noeud dans la Figure 2.4 ainsi que le coefficient de clustering global et le coefficient de transitivité.
- Pour le graphe de la Figure 2.5, étudier la limite du coefficient de clustering global et du coefficient de transitivité lorsque \(n\) tend vers l’infini.
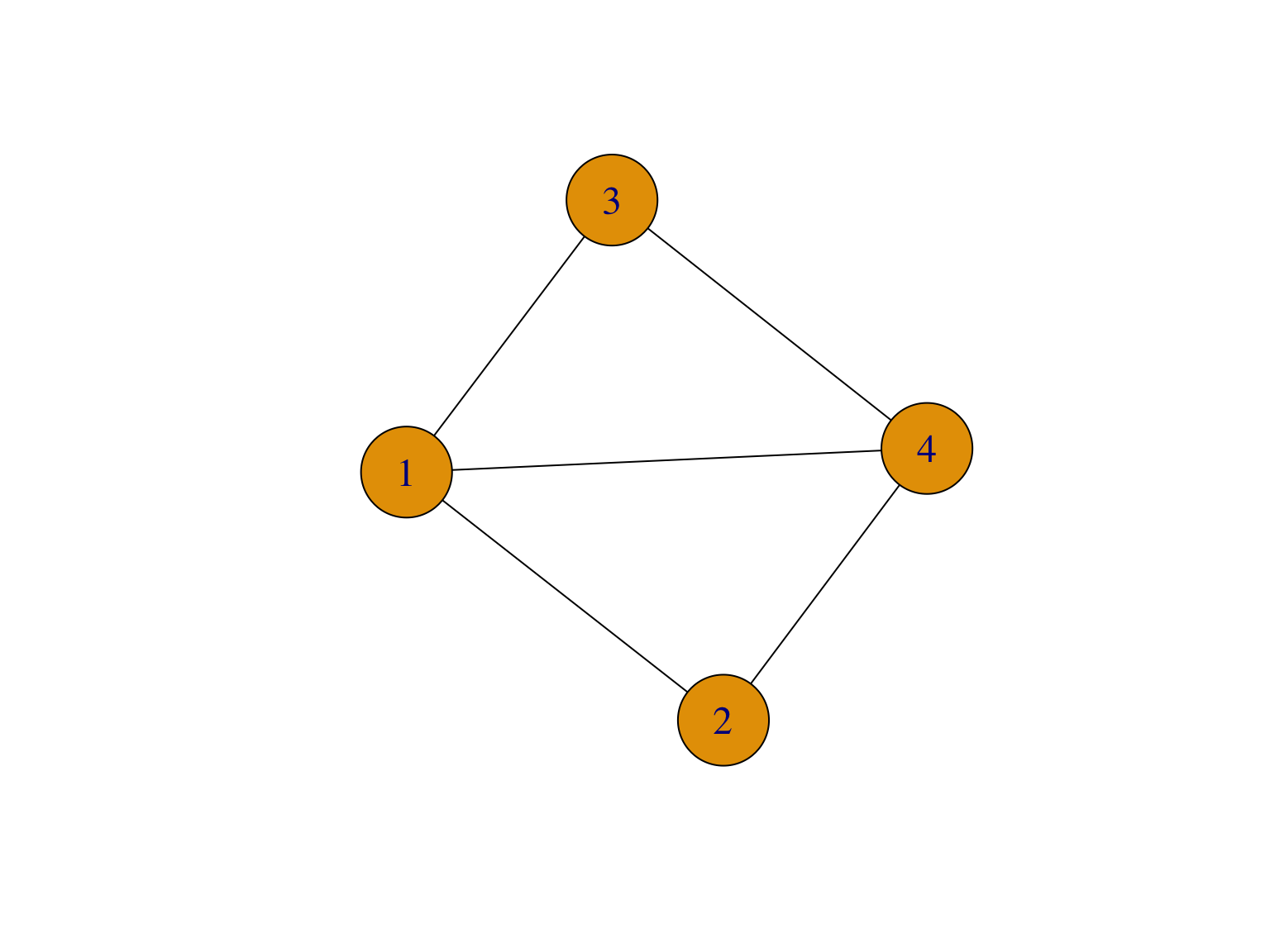
Figure 2.4: Graphe pour la Question 1 de l’exercice.
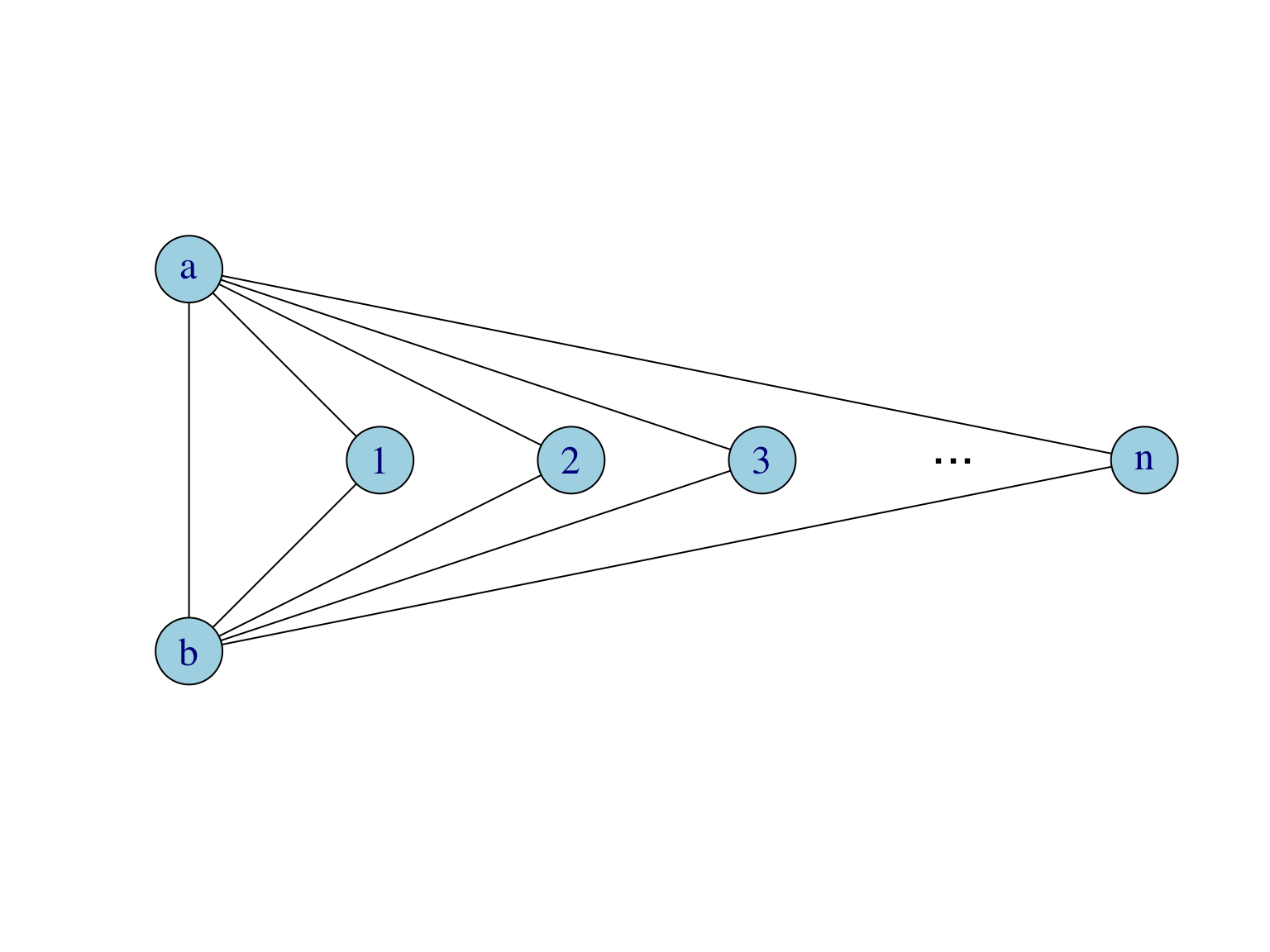
Figure 2.5: Graphe pour la Question 2 de l’exercice.