5.1 Graph cuts

Un point de vue alternatif à la recherche de communautés consiste à chercher à couper le graphe en sous-graphes en coupant le moins d’arêtes possibles.

Critère du mincut

Formellement, soient \(G\) un graphe et \(A\) la matrice d’adjacence associée. Pour \(k\) fixé, on cherche un partitionnement \(C_1,\dots,C_k\) des noeuds \(\{1,\dots,n\}\) en minimisant \[{\rm cut}(C_1,\dots,C_k):=\frac12\sum_{\ell=1}^kW(C_\ell,\bar C_\ell),\] où \(\bar C\) désigne le complémentaire de \(C\) et \(W\) est défini par \[W(U,V) = \sum_{i\in U,j\in V}A_{ij}.\]

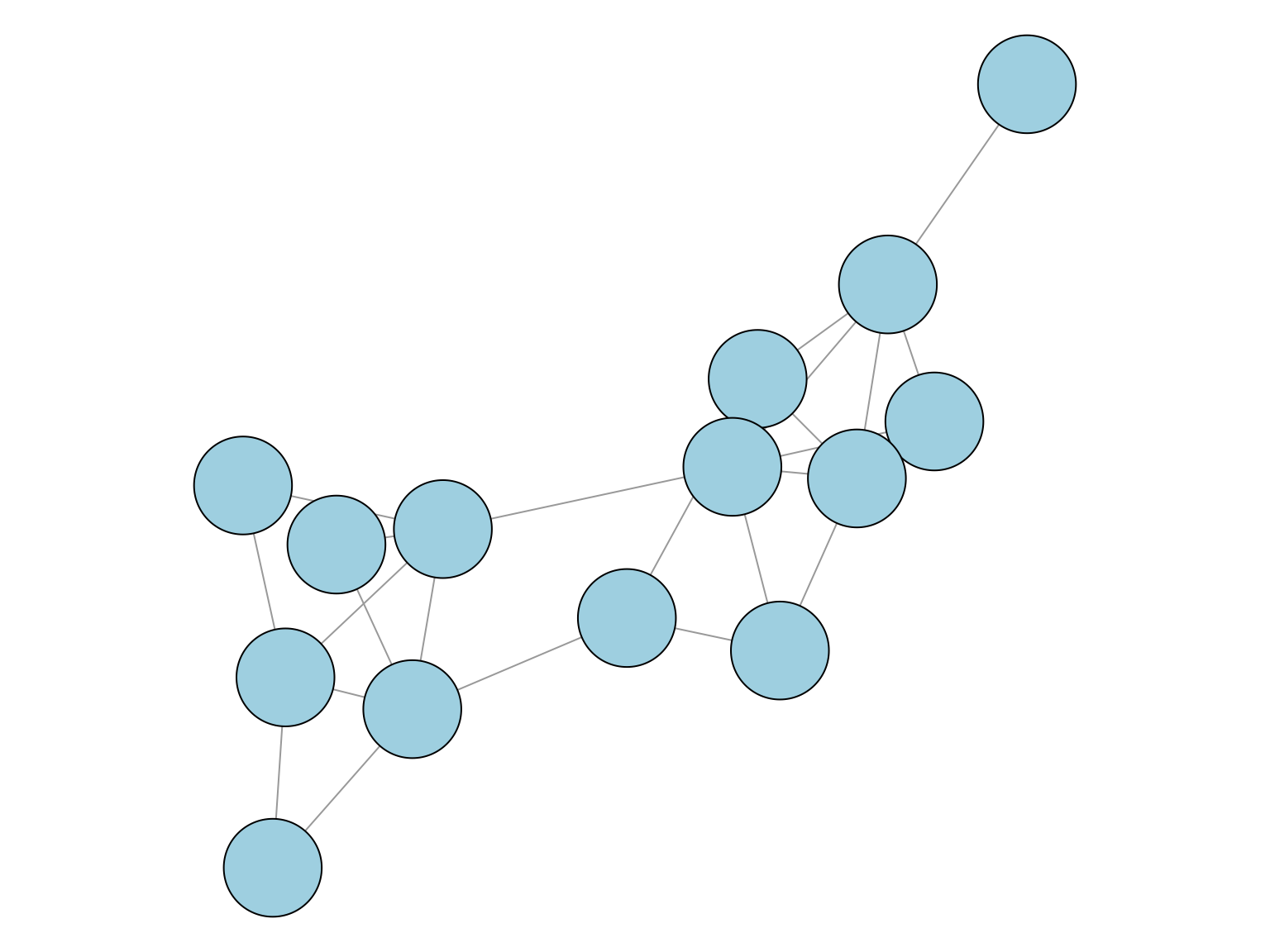
Figure 5.1: Graphe avec deux communautés et un noeud de degré 1.

En général, la solution du problème de mincut est peu satisfaisante, car des noeuds à faible degré sont simplement séparés du reste. Le simple mincut ne prend pas en compte la taille des clusters obtenus.

Il existe des variantes pour introduire des contraintes sur la taille des clusters.

Critère RatioCut

\[{\rm RatioCut}(C_1,\dots,C_k):=\frac12\sum_{\ell=1}^k\frac{W(C_\ell,\bar C_\ell)}{|C_\ell|}=\sum_{\ell=1}^k\frac{{\rm cut}(C_\ell,\bar C_\ell)}{|C_\ell|},\] où \(|C|\) dénote le cardinal de l’ensemble \(C\).

Critère NCut

\[{\rm NCut}(C_1,\dots,C_k):=\frac12\sum_{\ell=1}^k\frac{W(C_\ell,\bar C_\ell)}{{\rm vol}(C_\ell)}=\sum_{\ell=1}^k\frac{{\rm cut}(C_\ell,\bar C_\ell)}{{\rm vol}(C_\ell)},\] où \({\rm vol}(C)=\sum_{i\in C, j\in C}a_{ij}\) est la somme des poids des arêtes dans le sous-graphe induit par \(C\).

Lien avec le spectral clustering

Soit \(A\) une matrice d’adjacence d’un graphe non dirigé, et fixons le nombre de clusters à rechercher à \(k=2\). Soit \(f=(f_1,\dots,f_n)^T\) défini par \[\begin{align} f_i= \left\{\begin{matrix} \sqrt{|\bar C|/|C|},&\quad\text{si }i\in C\\ -\sqrt{| C|/|\bar C|},&\quad\text{si }i\notin C \end{matrix} \right. \tag{5.1} \end{align}\]

Exercice

1. Montrer que \(f\perp \mathbb 1\) et \(\|f\|=\sqrt n\). 2.Montrer que \[{\rm RatioCut}(C,\bar C)=\frac1nf^TLf,\] où \(L\) est la matrice laplacienne non normalisée du graphe.

 

En fait, le problem de minimisation \[\min_{C\subset V} {\rm RatioCut}(C,\bar C)\] est équivalent au problème

\[\begin{align*} \min_{C\subset V}&f^TLf \quad \text{ sous la contrainte: }\\ &f_i= \left\{\begin{matrix} \sqrt{|\bar C|/|C|},&\quad\text{si }i\in C\\ -\sqrt{| C|/|\bar C|},&\quad\text{si }i\notin C \end{matrix} \right., f\perp \mathbb 1, \|f\|=\sqrt n. \end{align*}\]

Ce dernier est un problème de minimisation discrète, car les entrées du vecteur \(f\) ne prennent que deux valeurs différentes.

En relâchant les contraintes, on peut considérer le problème \[ \min_{f\in\mathbb R^n} f^TLf \quad \text{ sous la contrainte } f\perp \mathbb 1, \|f\|=\sqrt n. \]

D’après le théorème de Rayleigh-Ritz, la solution de ce problème est donnée par le vecteur propre associé à la deuxième plus petite valeur propre de \(L\). La solution du problème du minRatioCut est donc approchée par ce vecteur propre. Afin d’en déduire un clustering, on fait un clustering des \(f_i\in\mathbb R\) en deux groupes \(A,\bar A\) (par k-means) et on pose \[C=\{i: f_i\in A\},\quad \bar C=\{i: f_i\in \bar A\}. \] On reconnait que c’est exactement ce que fait le clustering spectral non normalisé !

Ce résultat sur le lien entre le minRatioCut et le spectral clustering est établi quelque soit \(k\).

Quant au minNcut, par un raisonnement équivalent, on montre qu’en relâchant la contrainte d’un problème de minimisation discrète, on retrouve le spectral clustering normalisé basé sur \(L_N\).

En revanche, il n’y a pas de garantie que la solution du spectral clustering approche bien la solution minRatioCut (ou MinNcut) (sans relaxation). Au contraire, on peut être très loin…

Voir Luxburg (2007) pour plus de détails.

Exemple
Le graphe de la Figure 5.2 peut être partitionner en deux groupes de deux manière différente. Le partitionnement à gauche correspond à un nombre minimal de coupe avec deux groupes parfaitement equilibré. En revanche, le spectral clustering donnera le clustering de droite.

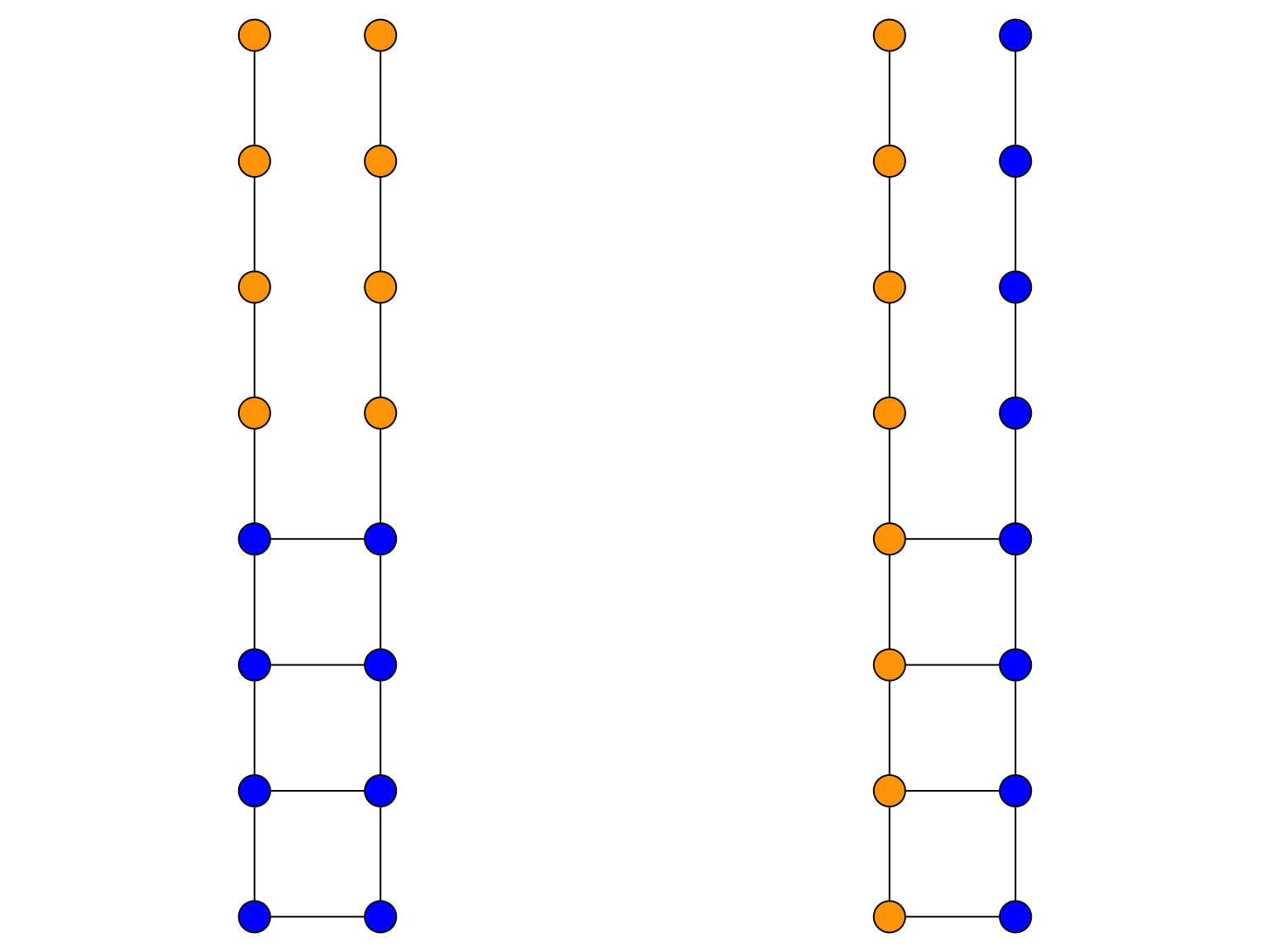
Figure 5.2: Graph ladder.

References

Luxburg, Ulrike von. 2007. “A Tutorial on Spectral Clustering.” Statistics and Computing 17 (4): 395–416. http://dx.doi.org/10.1007/s11222-007-9033-z.