8.1 Définition

Le modèle à blocs stochastique ou stochastic block model (SBM) est un modèle à variables latentes discrètes finies. L’idée est que chaque sommet a un profil de connexion décrit par sa variable latente. Ainsi, la probabilité d’une arête entre deux noeuds dépend des variables latentes associées à ses noeuds. De cette manière, on peut obtenir des graphes hétérogènes dont la distribution des degrés est p.ex. une loi de puissance.

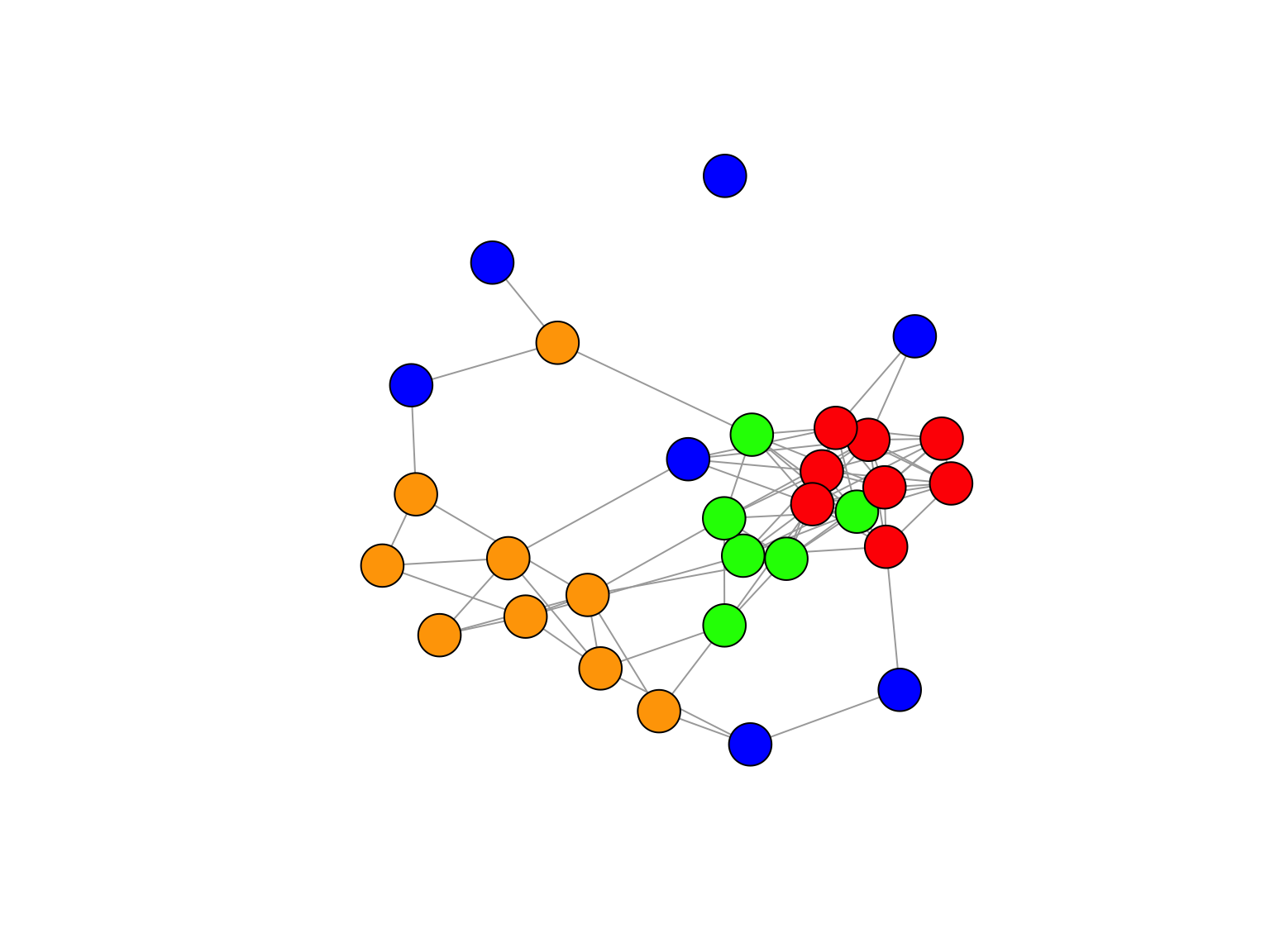
Exemple d’un SBM à 4 blocs. Les couleurs représentes les valeurs des variables latentes.

Figure 8.1: Exemple d’un SBM à 4 blocs. Les couleurs représentes les valeurs des variables latentes.

Les variables latentes \(\mathbf Z= \{Z_1,\ldots, Z_n\}\) sont indépendantes et identiquement distribuées, à valeurs finies dans \(\{1,\ldots,Q\}\) avec probabilités \(\mathbb P(Z_i=q)=\pi_q\). On note \(\boldsymbol \pi=(\pi_1,\ldots,\pi_Q)\) le paramètre des proportions des groupes. Il sera parfois pratique d’utiliser du one-hot encoding et de voir \(Z_i\) comme un vecteur de taille \(Q\) de la forme \(Z_i=(Z_{i1},\ldots, Z_{i,q})\) dont les coordonnées sont dans \(\{0,1\}\), somment à 1 et tel que \(Z_i\) est de loi multinomiale \(\mathcal{M}(1,\boldsymbol \pi)\).

On va décrire le modèle à blocs stochatiques dans le cadre d’un graphe non dirigé simple, mais les notations se généralisent facilement au cas dirigé et/ou avec des boucles. Notons donc l’ensemble d’observations par \(\mathbf A= \{A_{i,j}\}_{1 \le i, j \le n }\) constitué de variables aléatoires \(A_{i,j} \in \mathcal A\) (cas binaire ou valué), qui caractérisent les relations entre les noeuds \(i\) et \(j\).

Conditionellement aux variables latentes \(\mathbf Z= \{Z_i\}_{1\le i \le n}\), les variables \(\{A_{i,j}\}_{i<j}\) sont indépendantes et la distribution de chaque \(A_{i,j}\) ne dépend que de \(Z_i\) et \(Z_j\). On note \(F(\cdot; \gamma_{Z_i,Z_j})\) cette distribution conditionnelle, où \(\boldsymbol \gamma =(\gamma_{q,\ell})_{1\le q,\ell \le Q}\) est appelé paramètre de connectivité. C’est une matrice symétrique dans le cas d’un graphe non dirigé puisque \(\gamma_{q,\ell}= \gamma_{\ell q}\). Le paramètre \(\gamma_{q, \ell}\) décrit la loi des interactions entre des noeuds des groupes \(q\) et \(\ell\).

Ainsi, le modèle à blocs stochastiques est caractérisé par

  • \(\mathbf Z = (Z_1, \ldots, Z_n)\) variables latentes i.i.d. de loi \(\boldsymbol \pi\) sur \(\{1,\ldots,Q\}\),

  • \(\mathbf A=\{A_{i,j}\}_{i<j}\) ensemble d’observations à valeurs dans \(\mathcal A\) tel que

  • \(\mathbb P(\mathbf A|\mathbf Z) =\prod_{i<j}\mathbb P(A_{i,j} | Z_{i}, Z_j)\) (indépendance conditionnelle) et

  • pour tout \(i<j\) et pour tout \(1\le q,\ell \le Q,\) on a \[A_{i,j} | \{Z_{i}=q, Z_{j}=\ell \} \sim F(\cdot; \gamma_{q,\ell}).\]

On va distinguer à présent le SBM binaire (apparu dès le début des années 80 en Sciences Sociales) du cas valué (beaucoup plus récent).

SBM binaire. Dans le cas binaire, la loi conditionnelle de \(A_{i,j}\) sachant \((Z_i,Z_j)\) est simplement une loi de Bernoulli \(\mathcal{B}(\gamma_{Z_i,Z_j})\). Ainsi, \[\begin{equation*} F(y; \gamma) =\gamma^y (1-\gamma)^{1-y}\quad\text{pour tout } y \in \{0,1\}. \end{equation*}\] La Figure 8.1 en montre un exemple avec quatre blocs. On voit p.ex. que les noeuds rouges ont une forte probabilité de se connecter entre eux et aux noeuds verts, mais très peu aux jaunes et bleus. De manière générale, les bleus se connectent très peu à personne.

Notons qu’un SBM binaire avec un seul bloc, i.e. \(Q=1\), correspond au modèle \(G(n,p)\) avec \(p=\gamma_{1,1}\).

SBM valué. Pour les graphes valués, pour modéliser la loi conditionnelle de \(A_{i,j}\) sachant \(Z_i,Z_j\) on peut utiliser n’importe quelle loi paramétrique qui dépend seulement de \(Z_i,Z_j\) (ex: Poisson, Gaussienne, Laplace, \(\dots\)).

Cependant, si cette loi est absolument continue par rapport à la mesure de Lebesgue, on récupère un graphe valué dense, ce qui n’est pas toujours adéquat. Pour pallier ce problème, on introduit un mélange avec une masse de Dirac en 0, notée \(\delta_0(\cdot)\), qui modélise les arêtes absentes (zero-inflated model). Ainsi, \[\begin{equation*} \forall y \in \mathcal A, \quad F(y; \gamma) = \alpha G(y, \eta) +(1-\alpha) \delta_{0} (y), \end{equation*}\] où le paramètre de connectivité \(\gamma=(\alpha,\eta)\) avec \(\alpha \in [0,1]\) et \(G(\cdot,\eta)\) est la loi conditionnelle sur les valeurs des arêtes présentes.

Si tous les \(\alpha_{q \ell}\) valent 1, le graphe est dense (toutes les arêtes sont présentes). Ainsi les \(\alpha_{q \ell}\) sont des paramètres de densité du graphe. Si tous les \(\alpha_{q \ell}\) valent 0, on obtient un graphe vide, i.e. sans arêtes, ce qui n’est pas très intéressant.

Lorsque la loi \(G(\cdot,\eta)\) est une masse de Dirac en 1 (indépendante de \(\eta\)), on retrouve le SBM binaire. Le seul paramètre de la loi conditionnelle est alors \(\alpha\). Les cas classiques pour le choix de \(G\) sont: une loi de Poisson, une gaussienne (multivariée), etc.

Dans le cas non binaire, on peut (pour des raisons de parcimonie), supposer que tous les \(\alpha_{q \ell}\) sont constants (égaux à un certain \(\alpha\) fixé). Alors, la densité des arêtes est homogène dans le graphe, seule leur intensité (i.e. la valeur de \(A_{i,j}\)) va varier en fonction des groupes \((q,\ell)\).

Modèle d’affiliation. Le modèle d’affiliation ou planted partition model est un cas particulier du SBM avec des contraintes sur les paramètres. On suppose que le paramètre de connectivité \(\boldsymbol \gamma\) ne prend que deux valeurs différentes: une valeur intra-groupes et une valeur inter-groupes. Il s’agit d’un sous-modèle où on contraint: \[\begin{equation*} \mbox{pour tout } 1\le q,\ell\le Q, \quad \gamma_{q,\ell}=\left\{ \begin{array}{cc} \gamma_{\text{in}} & \text{ lorsque } q=\ell ,\\ \gamma_{\text{out}} & \text{ lorsque } q \neq \ell . \end{array} \right. \end{equation*}\] Dans le cas d’un graphe binaire, si on suppose en plus que \(\gamma_{\text{in}} \gg \gamma_{\text{out}}\), le graphe est structuré en communautés avec des groupes de noeuds fortement connectés entre eux. On dit que le graphe est assortatif. Dans le cas contraire où \(\gamma_{\text{out}} \gg \gamma_{\text{in}}\), le graphe a une structures de type multi-partie et on dit que le modèle est disassortatif.

Clustering des noeuds. Les variables latentes partionnent les noeuds en \(Q\) groupes. Ces groupes sont facilement interprétables, car l’appartenance à un groupe détermine le profil de connectivité d’un noeud. Ainsi, si on arrive à estimer les variables latentes, on a un clustering naturel des noeuds. Il est important de noter que ce clustering est beaucoup moins contraint que p.ex. la définition de groupes par communautés. Au fait, dans un SBM les noeuds d’un même groupe se connectent de la même façon entre eux et aux autres groupes.

Ces différences sont illustrées sur l’exemple jouet de la Figure 8.2. Pour le même graphe, on y voit deux partionnements différents: l’un par une méthode de détection de communautés, l’autre clustering ne peut être obtenu que par un SBM. Les deux clusterings sont valables et font du sens. D’ailleurs, les deux clusterings correspondent à des SBM: le premier à un modèle assortatif, le deuxième à un modèle disassortatif.

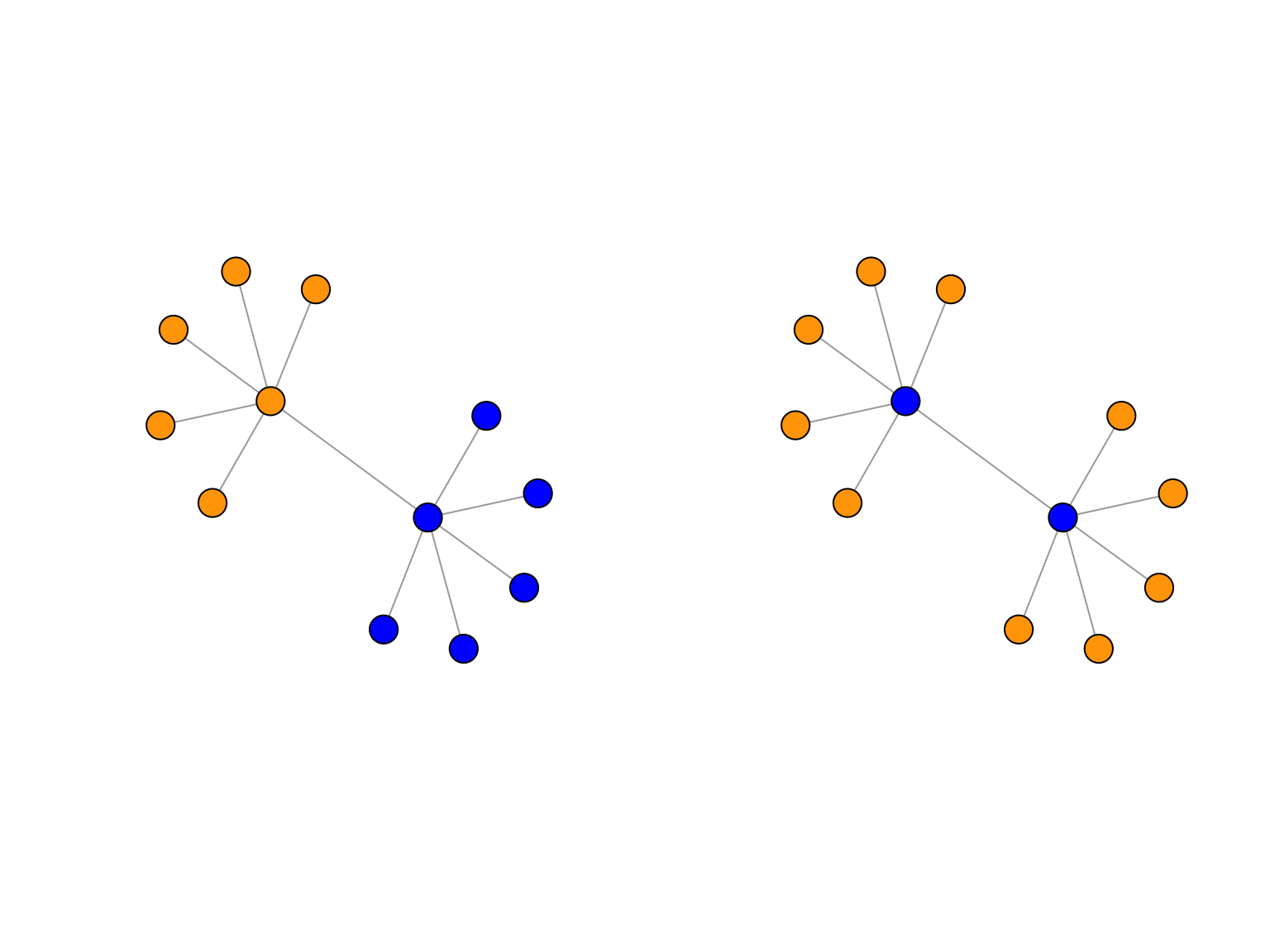
Deux partionnements différents pour les noeuds d'un même graphe. A gauche: des communautés. A droite: clustering par un SBM.

Figure 8.2: Deux partionnements différents pour les noeuds d’un même graphe. A gauche: des communautés. A droite: clustering par un SBM.

Interprétation des paramètres.

Les paramètres \(\boldsymbol \pi\) et \(\boldsymbol \gamma\) d’un SBM sont faciles à interpréter. Le vecteur \(\boldsymbol \pi=(\pi_1,\dots,\pi_Q)\) indique les proportions de noeuds dans les \(Q\) différents blocs. Les paramètres \(\boldsymbol \gamma\) est le paramètre de connectivité qui décrit précisément comment les noeuds se connectent en fonction de leur appartenance de bloc.

Prenons comme exemple le SBM de la Figure 8.1. Ici, les données ont été simulées avec des proportions de groupes égales, \(\pi_q=0,25\) pour \(q=1,\dots,4\). Comme il s’agit d’un SBM binaire, les paramètres de connectivité sont les paramètres de loi de Bernoulli. On a

gamma
##      [,1] [,2] [,3] [,4]
## [1,]  0.8  0.1  0.0  0.3
## [2,]  0.1  0.1  0.1  0.0
## [3,]  0.0  0.1  0.5  0.1
## [4,]  0.3  0.0  0.1  0.8

On voit alors que

  • les noeuds du deuxième groupe ne se connectent que très peu de manière générale,
  • le troisième bloc est une communauté,
  • le premier et le quatrième groupe ont une forte probabilité d’intra-connexion et en plus ils se connectent un peu à l’autre groupe.

On en déduit que le deuxième groupes sont les bleus et le troisième les jaunes. En prenant en compte que les jaunes ne se connectent pas du tout au premier groupe, on obtient que le premier groupe sont les rouges et le quatrième les verts.

Il existe une jolie visualisation des paramètres de connectivité. En fait, on peut considérer la matrice \(\boldsymbol \gamma\) comme la matrice d’adjacence d’un graphe pondéré à \(Q\) sommets avec des boucles. On l’appelle un métagraphe. On peut le tracer en variant la largeur des arêtes en fonction de leur poids donné par la matrice \(\boldsymbol \gamma\). Ainsi, pour le graphe de la Figure 8.1 on obtient le métagraphe de la Figure 8.3.

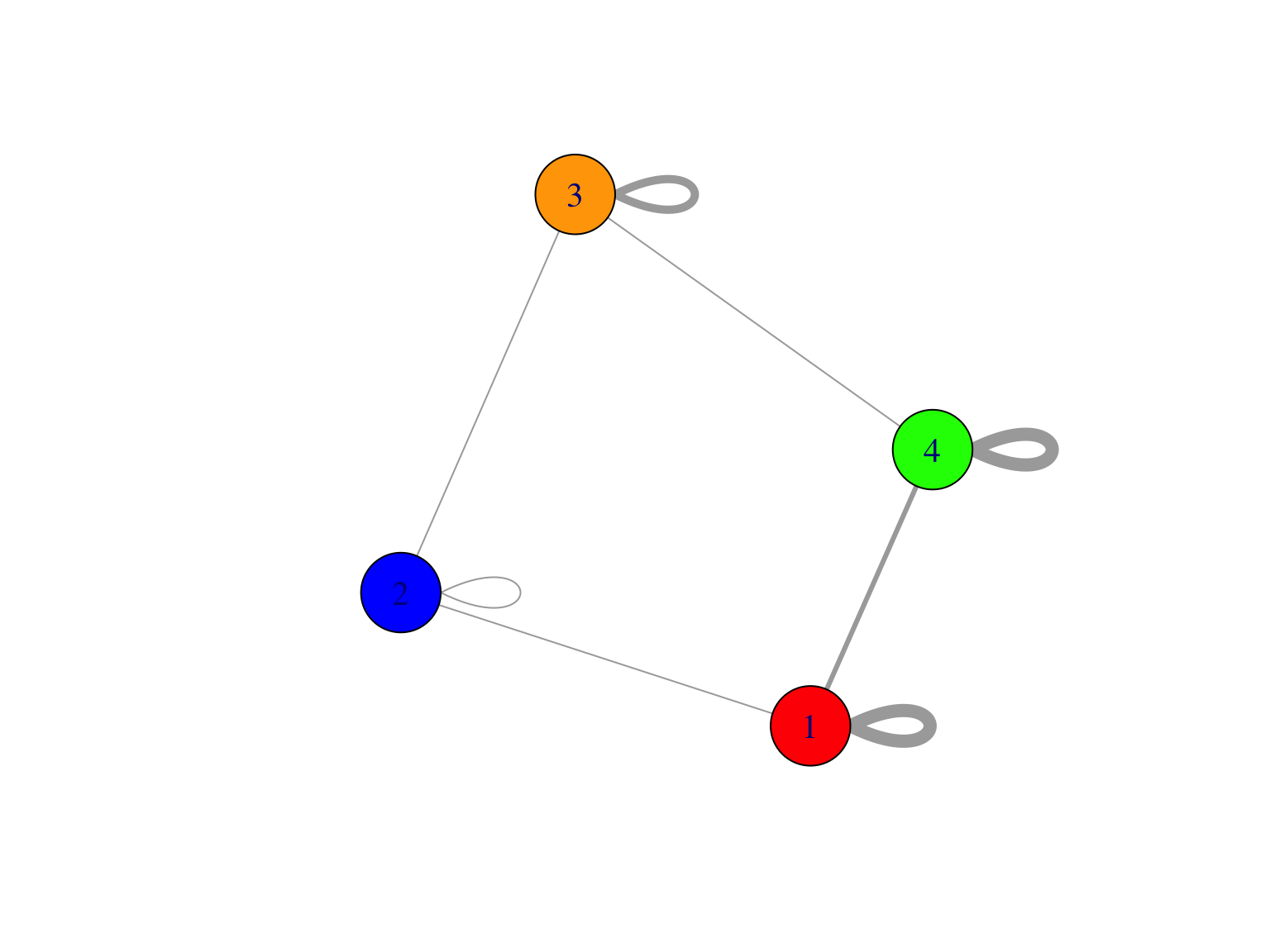
Métagraphe représentant le paramètre de connectivité du SBM de l’exemple.

Figure 8.3: Métagraphe représentant le paramètre de connectivité du SBM de l’exemple.

Notamment pour des grands graphes, le métagraphe peut aussi être vu comme un méthode de réduction de dimension, où tous les noeuds d’un groupe sont représentés par un seul sommet dans le nouveau graphe. Le nombre de blocs \(Q\) n’étant jamais très élevé, le métagraphe est facile à visualiser et à interpréter.