1.1 Exemples de graphes

Exemple de graphe composé de noeuds et d'arêtes.

Figure 1.1: Exemple de graphe composé de noeuds et d’arêtes.

Un graphe est composé d’un ensemble de sommets ou de noeuds qui sont reliés par des arêtes comme dans l’exemple de la Figure 1.1.

Voyons quelques exemples de domaines différents.

Historiquement, l’analyse des graphes s’est d’abord beaucoup développée en sciences sociales pour l’étude de réseaux sociaux: afin de mieux comprendre les interactions et dynamiques entre des personnes. Selon le contexte, un réseau social peut représenter des interactions physiques entre personnes, une base de données téléphoniques ou d’emails, ou un réseau social virtuel dans le plus grand est facebook (1.2).

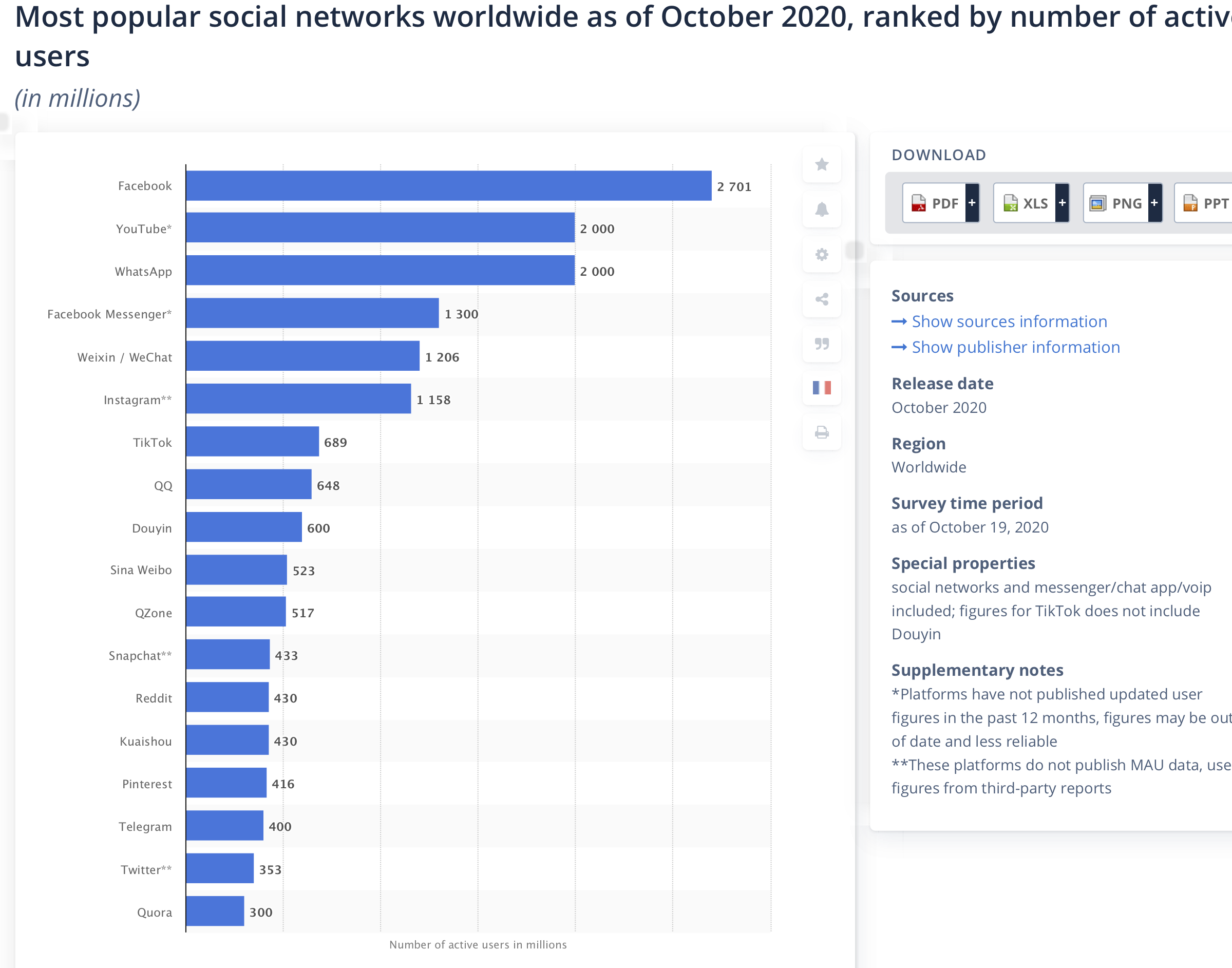
Source: www.statista.com.

Figure 1.2: Source: www.statista.com.

Internet est un réseau physique avec des routeurs connectés par des câbles ethernet ou des liaisons wifi. Mais aussi le world wide web est un réseau, dans lequel les pages web sont les noeuds et des hyperliens présents sur ces pages et qui pointent sur d’autres sont les arêtes (Figure 1.3).

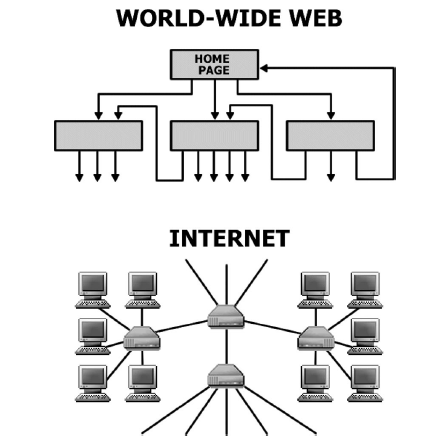
Internet et WWW. Source: Albert and Barabasi (2002).

Figure 1.3: Internet et WWW. Source: Albert and Barabasi (2002).

Dans les transports il y a des réseaux de métro (Figure 1.4), bus ou train, des réseaux aériens, réseaux routiers entre des villes, des réseaux avec des vélos en libre service…

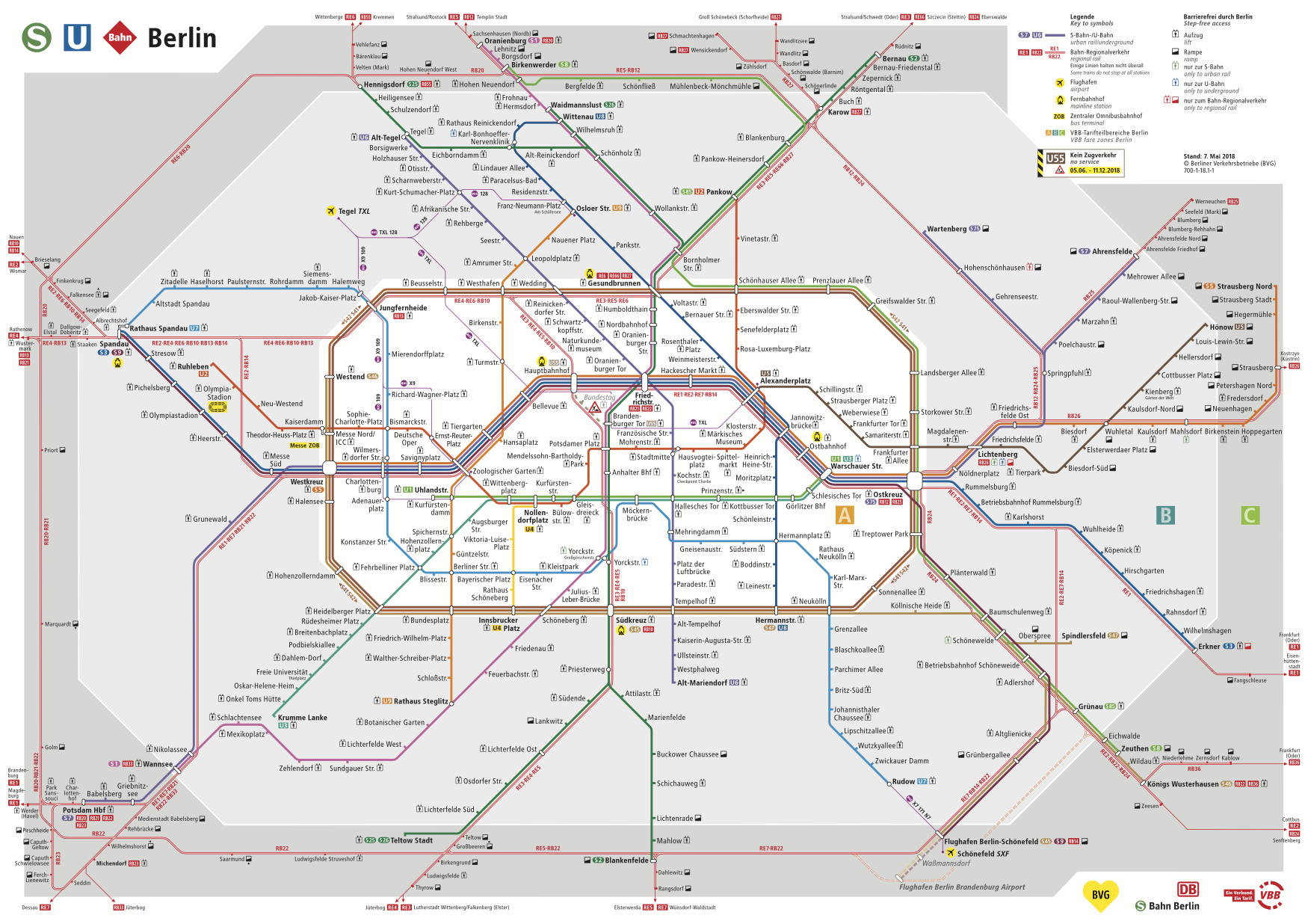
Réseau de métro à Berlin.

Figure 1.4: Réseau de métro à Berlin.

En écologie, on utilise des réseaux trophiques (ou foodweb) ou des réseaux plantes-pollonisateurs pour décrire des écosystèmes par les interactions entre espèces (Figure 1.5).

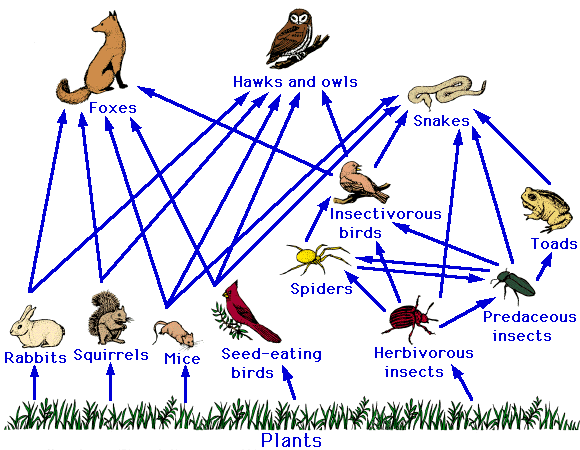
Réseau trophique simplifié. Une arête indique de qui une espèce est la proie.

Figure 1.5: Réseau trophique simplifié. Une arête indique de qui une espèce est la proie.

En médecine on utilise des réseaux pour étudier les interactions entre gènes au sein d’une cellule, même si l’interaction entre gènes se fait par l’intermédiaire physique de protéines ou ARN (Figure 1.6). Cela permet de mieux comprendre la dynamique cellulaire au niveau du génome, et mieux comprendre le système cellule dans sa complexité. On utilise également des réseaux pour décrire en détail les activités du cerveau, comme par exemple l’influence des gènes sur différentes parties du cerveau (Figure 1.7).

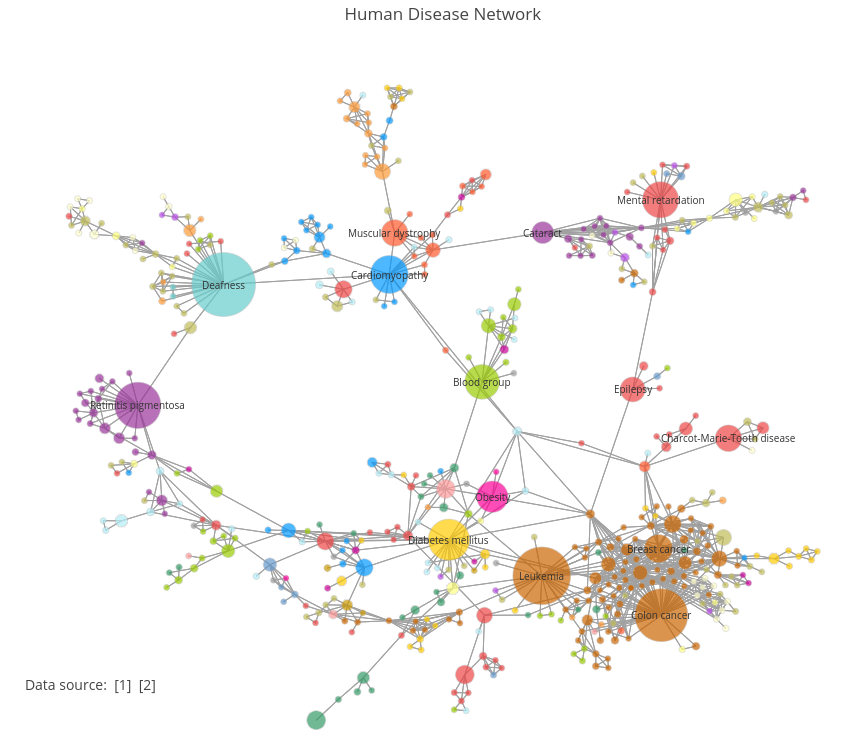
Réseau de régulation des gènes.

Figure 1.6: Réseau de régulation des gènes.

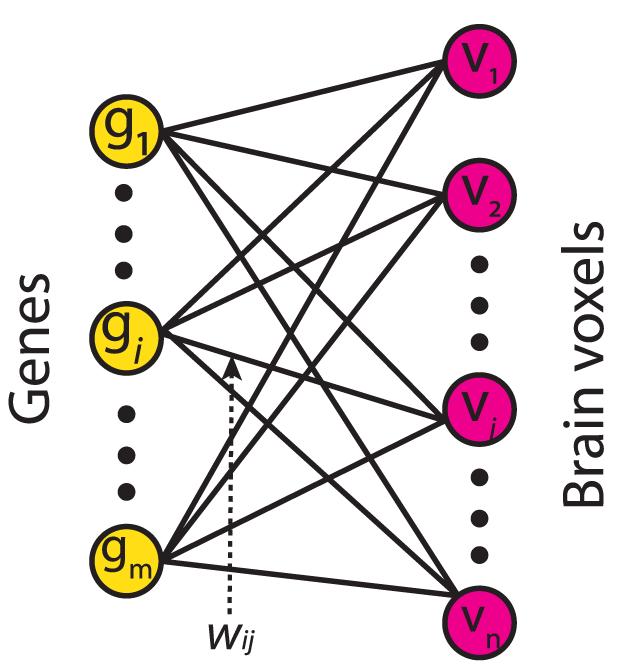
Source: Ji, Zhang, and Li (2014).

Figure 1.7: Source: Ji, Zhang, and Li (2014).

Néanmoins, soyons toujours vigilant et sceptique à toute visualisation de graphe, car elle peut être trompeuse. A titre d’exemple, Figure 1.8 représente le même réseau de deux manières différentes et le résultat n’est pas du tout le même. Ce problème est autant plus important que le graphe est grand. Nous voyons alors qu’en aucun cas l’analyse de graphe ne peut se contenter que de la visualisation du graphe, même si celle-ci peut s’avérer intéressante.

Deux représentations différentes du même réseau de blogs Kolaczyk and Csárdi (2014).Deux représentations différentes du même réseau de blogs Kolaczyk and Csárdi (2014).

Figure 1.8: Deux représentations différentes du même réseau de blogs Kolaczyk and Csárdi (2014).

References

Albert, Reka, and Albert-Laszlo Barabasi. 2002. “Statistical Mechanics of Complex Networks.” Rev. Mod. Phys. 74 (1): 47–97. https://doi.org/10.1103/RevModPhys.74.47.

Ji, Shuiwang, Wenlu Zhang, and Rongjian Li. 2014. “A Probabilistic Latent Semantic Analysis Model for Coclustering the Mouse Brain Atlas.” IEEE/ACM Transactions on Computational Biology and Bioinformatics 10 (6): 1460–8.

Kolaczyk, Eric D., and Gábor Csárdi. 2014. Statistical Analysis of Network Data with R. Use R! Springer, New York.