3.1 Modèle d’Erdös-Rényi

3.1.1 Définition

Un modèle de graphes aléatoires est une collection (finie ou pas) $\mathcal{G}$ de graphes et une loi de probabilité $\mathbb{P}$ sur cette collection $\mathcal{G}$.

Le modèle de graphe aléatoire le plus simple est le modèle introduit dans les années 1950 par Erdős and Rényi (1959). Il s’agit de la collection $\mathcal{G}{(n,M)}$ de tous les graphes simples non dirigés d’ordre $n$ et de taille $M$, munie de la loi uniforme $\mathbb{P}$ sur cette collection. Ainsi, la collection $\mathcal{G}{(n,M)}$ contient $\binom{N}{M}$ graphes différents, où $N=n(n-1)/2$ et la probabilité de chacun d’eux est $1/\binom{N}{M}$.

Le modèle $\mathcal{G}{(n,M)}$ contient alors tous les graphes à $n$ noeuds est dans la densité est égale à $M/N$. Ce modèle est d’une grande simplicité, mais il a au moins deux inconvénients importants: la simulation dans ce modèle n’est pas simple, et l’analyse des propriétés statistiques non plus.

Une variante plus commune de ce modèle qui n’a pas ces défauts est le modèle ${G}(n,p)$.

Definition 3.1 On définit la collection ${G}(n,p)$ de graphes simples non dirigés générés selon un modèle à deux paramètres: $n$ le nombre de noeuds du graphe et $p\in (0,1)$ la probabilité de connection de deux noeuds pris au hasard. C’est un graphe dont toutes les arêtes $A_{ij} , 1\le i <j \le n$ sont des variables aléatoires indépendantes de loi de Bernoulli $\mathcal{B}(p)$.

La définition s’adapte directement aux graphes dirigés en cosidérant toutes les arêtes $\{A_{i,j\}_{i\neq j}}$ comme des variables aléatoires indépendantes et identiquement distribuées.

Lorsque $n$ est grand et $M\approx \binom n 2 p$, les deux modèles $\mathcal G(n,M)$ et $G(n,p)$ sont équivalents. Souvent on réfère au modèle $G(n,p)$ comme le modèle d’Erdös-Rényi.

Pour simuler un graphe du modèle $G(n,p)$, on n’a qu’à simuler des variables Bernoulli. Il ne peut pas y avoir de plus simple.

De même pour l’analyse statistique du modèle: il faut essentiellement savoir manipuler des variables Bernoulli i.i.d.

Exercice. Soit $n$ et $p$ fixés. Considérons le modèle de graphe $G(n,p)$.

Donner le nombre moyen d’arêtes dans un graphe $G(n,p)$.
Soit $M\geq 0$. Quelle est la probabilité que le graphe est de taille $M$?
Donner la loi de la variable aléatoire $D_i$ qui désigne le degré du noeud $i$ dans le modèle $G(n,p)$. En déduire l’espérance du degré $D_i$.
Etudier la convergence de $\bar{D}_n/(n-1)$ lorsque $n\to\infty$, où $\bar{D}_n$ désigne le degré moyen du graphe $G(n,p)$.
Donner une approximation de la loi de $D_i$ lorsque $n$ est grand.

Lorsqu’on considère une suite de graphes $G(n,p_n)$, on suppose typiquement que $(p_n)_n$ est décroissante, sinon les graphes associés sont trop denses pour modéliser des grands graphes réels. Pour ces suites de graphes, on peut étudier le phénomène de transition de phase , i.e. on veut savoir à partir de quelle suite $(p_n)_n$ certains motifs apparaissent dans le graphe lorsque $n$ tend vers l’infini.

Exercice. Soit $F$ un motif avec $k$ sommets et $\ell$ arêtes. %Pour quelle probabilité $p_n$ le graphe $G(n,p_n)$ contient au moins un motif $F$ (lorsque $n$ est grand)? Notons $X_n$ le nombre de motif $F$ dans un graphe $G(n,p_n)$.

Montrer que \[\mathbb E[X_n]=C_n^k\frac{k!}{a}p_n^l\approx \frac{n^kp_n^l}a,\] où $a$ est le nombre de permutations de $k$ noeuds du motif $F$ tel que le graphe obtenu par permutation est isomorphe (le même motif).
Montrer que si $p_n=o(n^{-k/l})$, alors \[\lim_{n\to\infty}\mathbb P(X_n=0)=1.\]

D’après Bollobás (1985) on a aussi: si $p_n=c_nn^{-k/l}$ avec $c_n\to\infty$, alors \[\lim_{n\to\infty}\mathbb P(X_n>0)=1.\]

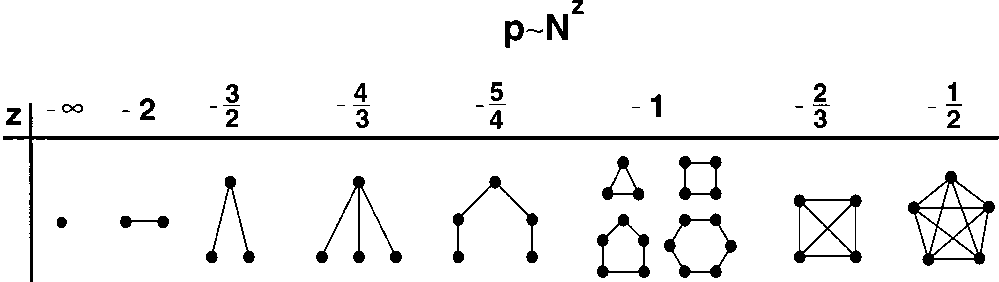
$Transition de phase dans un $G(n,p_n)$. Figure tirée de Albert and Barabasi (2002) où $N$ désigne le nombre de sommets.$

Figure 3.1: Transition de phase dans un $G(n,p_n)$. Figure tirée de Albert and Barabasi (2002) où $N$ désigne le nombre de sommets.

Figure 3.1 illustre le résultat. En particulier, si $p_n=n^z$ avec $z<-2$, le graphe $G(n,p)$ est essentiellement composé de noeuds isolés. Pour $-2<z<\frac32$ des arêtes apparaissent, ensuite des arbres. A partir de $z>-1$ on observe des cycles, et il faut $z>-\frac23$ pour voir apparaître les premiers cliques d’ordre 4.

3.1.2 Simulation de grands graphes

Pour simuler un graphe du modèle $G(n,p)$, il suffit, en principe, de générer $n \choose 2$ variables aléatoires de Bernoulli de paramètre $p$. Lorsque $n$ est grand et $p=p_n$ de l’ordre de $1/n$, cette procédure est très inefficace: l’espérance du degré d’un noeud est finie et donc la plupart des variables valent 0.

Dans ce cas, il est plus efficace de simuler d’abord le nombre $M$ d’arêtes présentes dans le graphe selon une loi binomiale Bin$(N,p)$, et ensuite tirer les positions des arêtes, i.e. tirer sans remise $M$ positions parmi les $N$ arêtes possibles. La complexité de calcul est alors en $O(n+|E|)$ au lieu de $O(n^2)$, voir Kolaczyk (2009), section 6.2.3 pour plus de détails.

3.1.3 Distribution des degrés

Rappelons que pour un graphe simple binaire et non dirigé, le degré $D_i$ du noeud $i$ pour $i=1, \dots, n$ et le degré moyen $\bar {D}$ du graphe vérifient la relation suivante \[ D_i = \sum_{j\neq i} A_{ij} , \quad \text{ et } \bar{D} = \frac 1 n \sum_{i=1}^n D_i = \frac 1 n \sum_{i=1}^n \sum_{j\neq i} A_{ij} =\frac{2 |E|}{n}. \] Les degrés $\{D_i\}_{i =1,\dots, n}$ des noeuds d’un graphe sont des variables aléatoires, non indépendantes en général. On s’intéresse ici à la distribution marginale de ces variables.

Dans le cas de $G(n,p)$, le degré $D_i$ du noeud $i$ suit une loi binomiale, à savoir \[ D_i \sim \mathcal{B}(n-1,p). \] Par la loi des grands nombres, la variable $\bar{D}/(n-1)$ converge vers $\mathbb E(A_{ij})=p$. En particulier, l’espérance du degré d’un noeud vérifie $\mathbb E(D_i)=(n-1)p =pn(1+o(1))$ (lorsque $n$ grand, $p$ petit).

La loi binomiale comme la loi de Poisson sont des lois à queues légères impliquant qu’il y a très peu de valeurs extrêmes. Or, les réseaux réels sont typiquement très hétérogènes contenant un petit nombre de noeuds avec un degré très fort, les hubs. Ceci est une première indication que le modèle d’Erdös-Rényi s’ajuste mal sur des graphes issus d’applications pratiques.

Coefficient de clustering.

Dans $G(n,p)$, puisque toutes les arêtes sont indépendantes, la probabilité que deux voisins d’un noeud $i$ soient connectés vaut $p$. Donc en moyenne, $\mathbb E(2|E_i|\, \big| D_i)=pD_i(D_i-1)$ ce qui donne $\mathbb E(C_i)=p$ et $\mathbb E(\bar{C})=p\simeq \mathbb E(D_i)/n\simeq \bar{d}/n$. En conséquence, dans $G(n,p)$, le rapport $\bar{c}/\bar{d}$ doit être de l’ordre de $1/n$. Dans les graphes réels, on observe plutôt un rapport constant.

Distance Pour $G(n,p)$, on peut montrer que la valeur typique de la distance $\ell_{ij}$ est de l’ordre de $\log(n)$, donc les graphes $G(n,p)$ sont des graphes petit monde.

3.1.4 Mauvais ajustement aux réseaux réels

Bien que le modèle $G(n,p)$ d’Erdös-Rényi est un modèle mathématique très étudié, avec de nombreuses propriétés très intéressantes, il s’ajuste mal aux réseaux observés. Son principal défaut est que le modèle $G(n,p)$ produit des graphes homogènes, alors que la vaste majorité de graphes réels sont assez hétérogènes.

En revanche, l’idée de modéliser les arêtes par des variables aléatoires permet de définir facilement d’autres modèles de graphes plus appropriés pour l’analyse de graphes réels, cf. Chapitre 8.

References

Albert, Reka, and Albert-Laszlo Barabasi. 2002. “Statistical Mechanics of Complex Networks.” Rev. Mod. Phys. 74 (1): 47–97. https://doi.org/10.1103/RevModPhys.74.47.

Bollobás, B. 1985. Random Graphs. Academic, London.

Erdős, P., and A. Rényi. 1959. “On Random Graphs. I.” Publicationes Mathematicae 6: 290–97.

Kolaczyk, Eric D. 2009. Statistical Analysis of Network Data: Methods and Models. Springer.